このページは、数研出版:数学Ⅲ[708]
第1章 関数
第1章 関数

教科書の復習から入試の入門まで|数学入門問題精講
旺文社の入門問題精講シリーズの紹介高校生の皆さん、数学の勉強に困ったことはありませんか?教科書の内容...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
数研出版数学Ⅲ 第1章 関数
数研出版数学Ⅲ 第2章 極限
数研出版数学Ⅲ 第3章 微分法
数研出版数学Ⅲ 第4章 微分法の応用
数研出版数学Ⅲ 第5章 積分法
数研出版数学Ⅲ 第6章 積分法の応用
第1章 関数
1 分数関数
p.8 練習1\({\small (1)}~\)




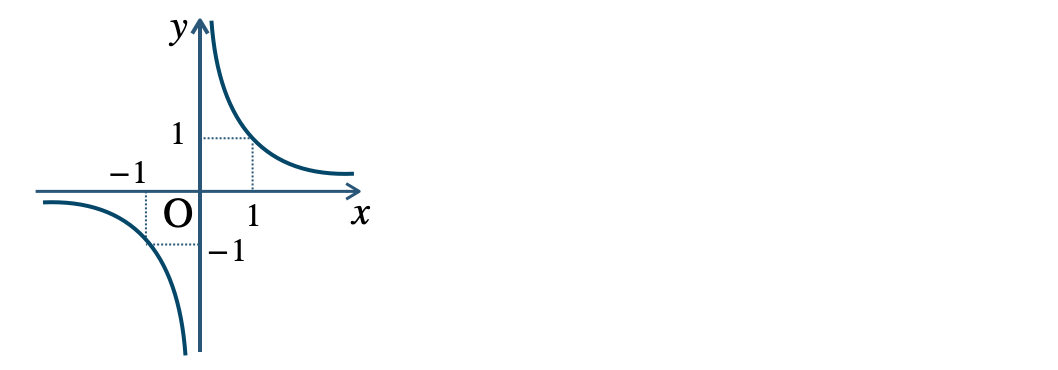
\({\small (2)}~\)
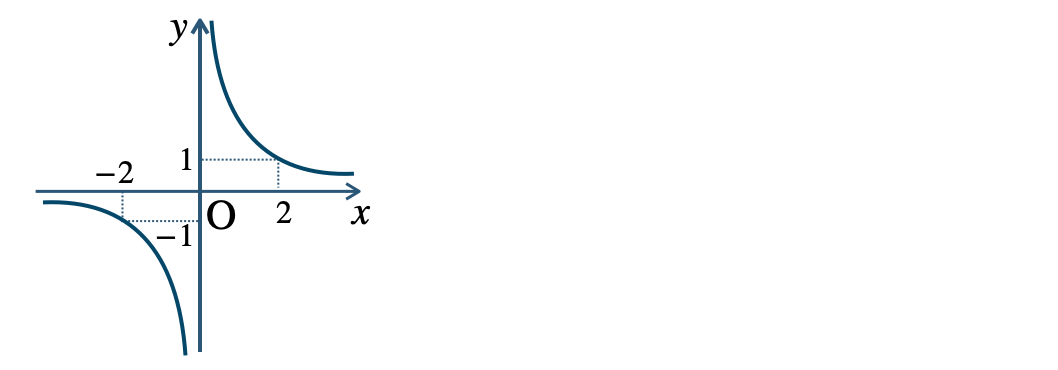
\({\small (3)}~\)

\({\small (4)}~\)
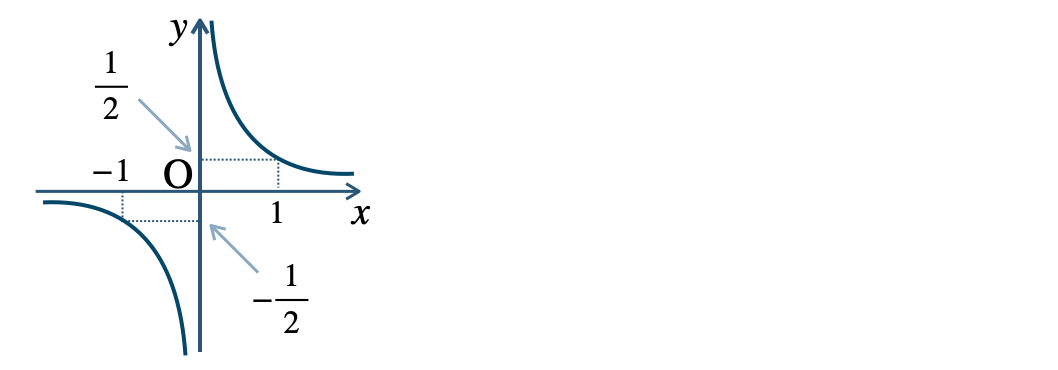
p.9 練習2\({\small (1)}~\)定義域 \(x\neq 0\)、値域 \(y\neq -1\)




\({\small (2)}~\)定義域 \(x\neq -2\)、値域 \(y\neq 0\)

\({\small (3)}~\)定義域 \(x\neq 1\)、値域 \(y\neq 2\)
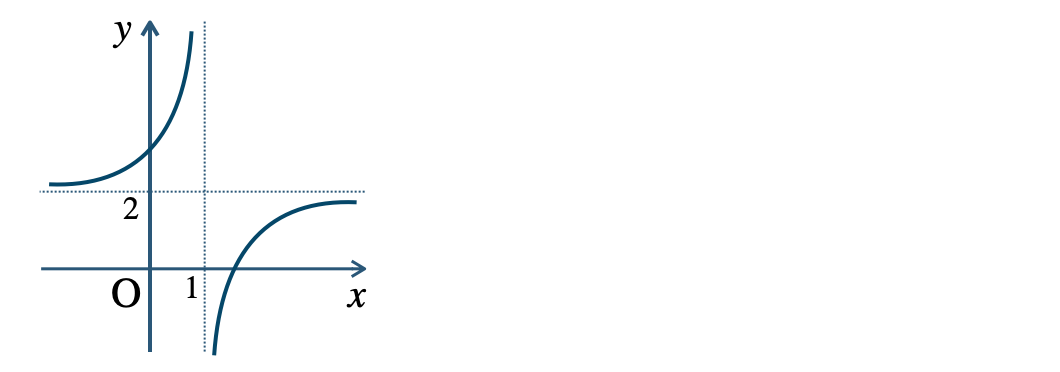
p.10 問1定義域 \(x\neq 2\)、値域 \(y\neq 3\)

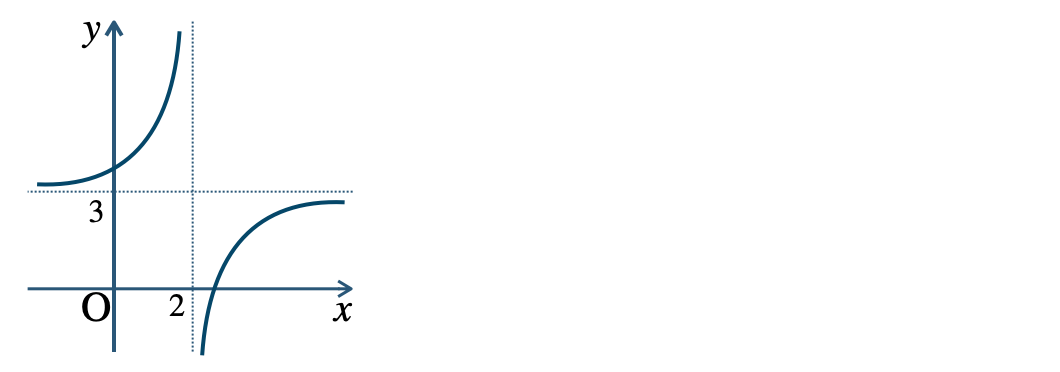
p.10 練習3\({\small (1)}~\)定義域 \(x\neq -3\)、値域 \(y\neq 2\)




\({\small (2)}~\)定義域 \(x\neq 1\)、値域 \(y\neq -2\)
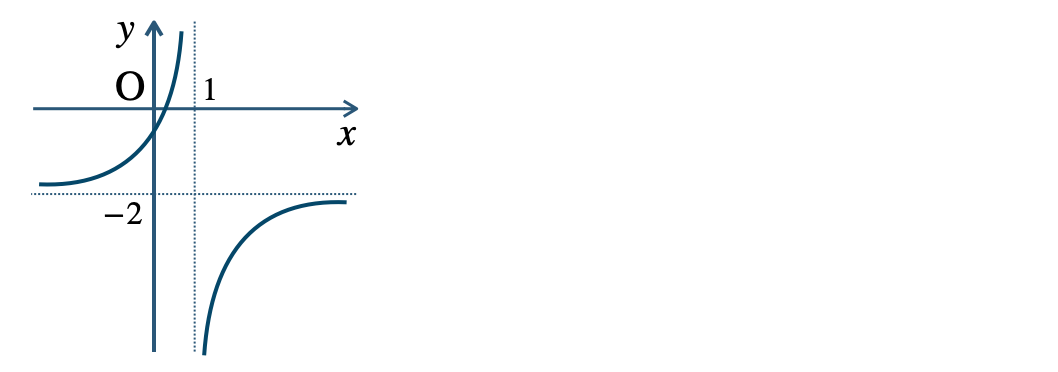
\({\small (3)}~\)定義域 \(x\neq {\large \frac{\,1\,}{\,2\,}}\)、値域 \(y\neq 2\)
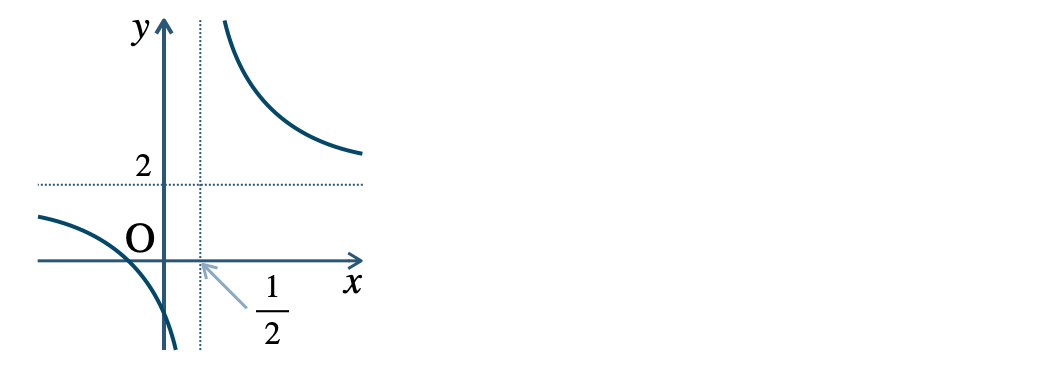
p.11 練習4$${\small (1)}~(0~,~0)~,~(2~,~4)$$$${\small (2)}~(-1~,~-3)~,~(1~,~1)$$
p.11 問2$$~~~x< -1~,~1< x < 2$$
p.11 練習5$${\small (1)}~x=-4~,~1$$$${\small (2)}~x< -4~,~-2< x < 1$$
2 無理関数
p.13 問3 \(x\) 軸に関して対称
p.13 練習6\({\small (1)}~\)\(y\) 軸に関して対称



\({\small (2)}~\)原点に関して対称

p.13 練習7\({\small (1)}~\)定義域 \(x≧0\)、値域 \(y≧0\)



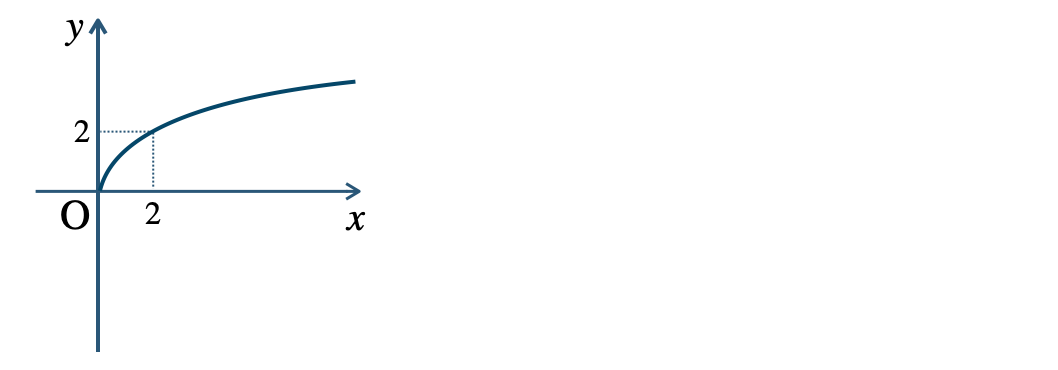
\({\small (2)}~\)定義域 \(x≧0\)、値域 \(y≦0\)

\({\small (3)}~\)定義域 \(x≦0\)、値域 \(y≦0\)

p.14 練習8\({\small (1)}~\)定義域 \(x≧-2\)、値域 \(y≧0\)


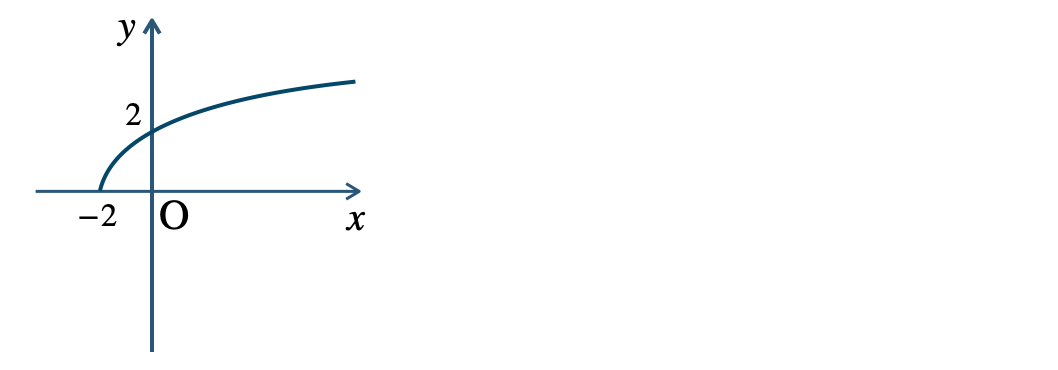
\({\small (2)}~\)定義域 \(x≦1\)、値域 \(y≦0\)

p.14 問4$$~~~1≦y≦\sqrt{5}$$
p.14 練習9$$~~~\sqrt{3}< y≦3$$
p.15 練習10$${\small (1)}~(3~,~3)$$$${\small (2)}~(1~,~1)~,~(5~,~3)$$
p.15 問5$$~~~-2≦x <2$$
p.15 練習11$${\small (1)}~x=0$$$${\small (2)}~-1≦x < 0$$
3 逆関数と合成関数
p.17 練習12$${\small (1)}~y=2x+4$$$${\small (2)}~y=-\frac{\,1\,}{\,3\,}x+\frac{\,1\,}{\,3\,}$$
p.17 練習13$$~~~y=-\frac{\,1\,}{\,3\,}x+\frac{\,4\,}{\,3\,}~~~(-2≦x≦7)$$
p.18 練習14$${\small (1)}~y=-\sqrt{x}$$$${\small (2)}~y=\sqrt{x+2}$$
p.18 練習15$${\small (1)}~y=-\frac{\,x-1\,}{\,x-2\,}$$$${\small (2)}~y=\frac{\,3x+4\,}{\,x+1\,}$$
p.19 練習16$$~~~a=2~,~b=-1$$
p.19 練習17$${\small (1)}~y=-x^2~~~(x≧0)$$


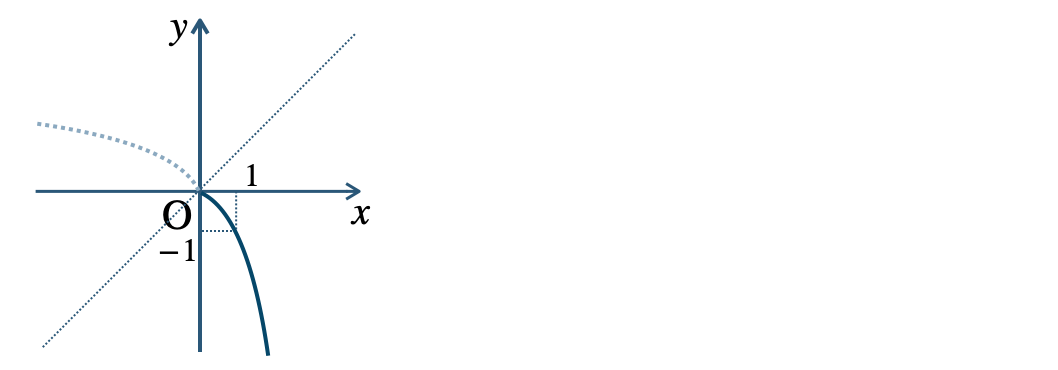
$${\small (2)}~y=\sqrt{2x}~~~(2≦x≦8)$$
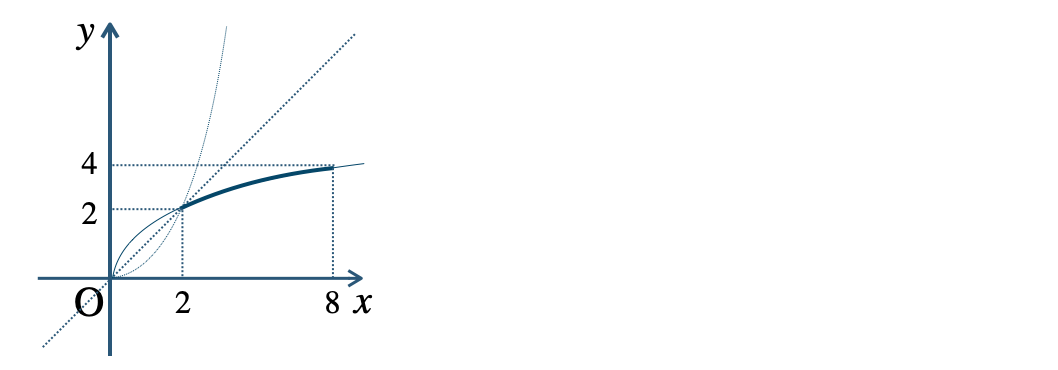
p.20 練習18$${\small (1)}~y=\log_{\frac{\,1\,}{\,2\,}}x$$



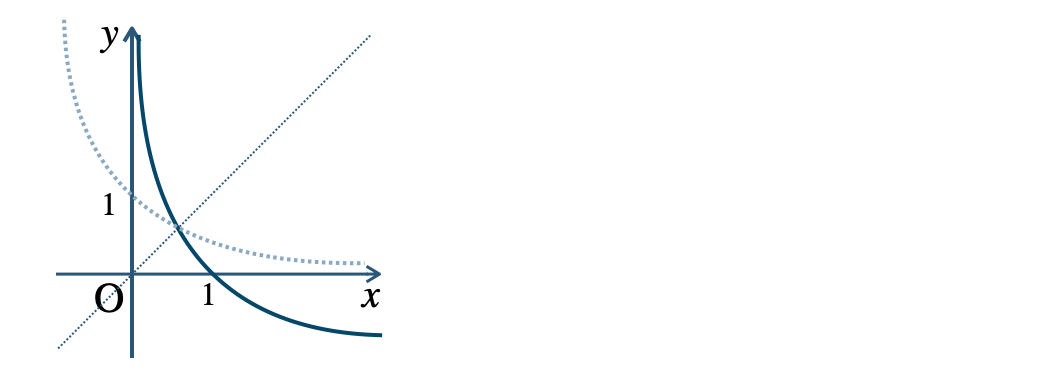
$${\small (2)}~y=3^x$$

$${\small (3)}~y=2^{x-1}$$

p.21 練習19$${\small (1)}~(g \circ f)(x)=|x+1|+1$$$${\small (2)}~(f \circ g)(x)=|x|+2$$$${\small (3)}~(h \circ g)(x)=\log_{2}(|x|+1)$$
問題
p.22 問題6[証明] \(y=\sqrt{x-1}\) とすると、値域は \(y≧0\)
これより、\(x\) について解くと、$$\begin{eqnarray}~~~y&=&\sqrt{x-1}\\[2pt]~~~y^2&=&x-1\\[2pt]~~~x&=&y^2+1\end{eqnarray}$$よって、逆関数は$$~~~y=x^2+1~~~(x≧0)$$これより、$$~~~f^{-1}(x)=x^2+1~~~(x≧0)$$したがって、$$\begin{eqnarray}~~~(f^{-1}\circ f)(x)&=&(\sqrt{x-1})^2+1\\[2pt]~~~&=&x\end{eqnarray}$$[終]
これより、\(x\) について解くと、$$\begin{eqnarray}~~~y&=&\sqrt{x-1}\\[2pt]~~~y^2&=&x-1\\[2pt]~~~x&=&y^2+1\end{eqnarray}$$よって、逆関数は$$~~~y=x^2+1~~~(x≧0)$$これより、$$~~~f^{-1}(x)=x^2+1~~~(x≧0)$$したがって、$$\begin{eqnarray}~~~(f^{-1}\circ f)(x)&=&(\sqrt{x-1})^2+1\\[2pt]~~~&=&x\end{eqnarray}$$[終]
演習問題B
p.23 演習問題B 6[証明] \(a^2+bc\neq 0~,~c\neq 0\) より、$$\begin{eqnarray}~~~y&=&\frac{\,ax+b\,}{\,cx-a\,}
\\[3pt]~~~&=&\frac{\,a^2+bc\,}{\,c^2\left( x-\frac{\,a\,}{\,c\,} \right)\,}+\frac{\,a\,}{\,c\,}
\end{eqnarray}$$これより、定義域 \(x\neq {\large \frac{\,a\,}{\,c\,}}\)、値域 \(y\neq {\large \frac{\,a\,}{\,c\,}}\)
\(x\) について解くと、$$\begin{eqnarray}~~~y&=&\frac{\,ax+b\,}{\,cx-a\,}
\\[3pt]~~~y(cx-a)&=&ax+b
\\[2pt]~~~(cy-a)x&=&ay+b
\end{eqnarray}$$\(cy-a\neq 0\) より、$$~~~x=\frac{\,ay+b\,}{\,cy-a\,}$$よって、逆関数は$$~~~y=\frac{\,ax+b\,}{\,cx-a\,}$$したがって、\(f(x)\) の逆関数 \(f^{-1}(x)\) は \(f(x)\) に等しい [終]
\\[3pt]~~~&=&\frac{\,a^2+bc\,}{\,c^2\left( x-\frac{\,a\,}{\,c\,} \right)\,}+\frac{\,a\,}{\,c\,}
\end{eqnarray}$$これより、定義域 \(x\neq {\large \frac{\,a\,}{\,c\,}}\)、値域 \(y\neq {\large \frac{\,a\,}{\,c\,}}\)
\(x\) について解くと、$$\begin{eqnarray}~~~y&=&\frac{\,ax+b\,}{\,cx-a\,}
\\[3pt]~~~y(cx-a)&=&ax+b
\\[2pt]~~~(cy-a)x&=&ay+b
\end{eqnarray}$$\(cy-a\neq 0\) より、$$~~~x=\frac{\,ay+b\,}{\,cy-a\,}$$よって、逆関数は$$~~~y=\frac{\,ax+b\,}{\,cx-a\,}$$したがって、\(f(x)\) の逆関数 \(f^{-1}(x)\) は \(f(x)\) に等しい [終]
次のページ「第2章 極限」


