【新課程】数研出版：数学Ⅲ[708]

p.106 練習1$${\small (1)}~y=-2x-4$$$${\small (2)}~y=\frac{\,\sqrt{3}\,}{\,2\,}x-\frac{\,\sqrt{3}\pi\,}{\,12\,}+\frac{\,1\,}{\,2\,}$$

p.107 練習2$${\small (1)}~y=\frac{\,1\,}{\,e\,}x+e+\frac{\,1\,}{\,e\,}$$$${\small (2)}~y=-\frac{\,1\,}{\,2\,}x+\frac{\,\pi\,}{\,8\,}+1$$

p.108 練習3$${\small (1)}~y=-4x+4~,~\left(\frac{\,1\,}{\,2\,}~,~2\right)$$$$~~~~y=-4x-4~,~\left(-\frac{\,1\,}{\,2\,}~,~-2\right)$$$${\small (2)}~y=-\frac{\,1\,}{\,9\,}x-\frac{\,2\,}{\,3\,}~,~\left(-3~,~-\frac{\,1\,}{\,3\,}\right)$$$$~~~~y=-x+2~,~(1~,~1)$$

p.108 練習4$${\small (1)}~y=x-1~,~(1~,~0)$$$${\small (2)}~y=(\log_{}2+1)x-2~,~(2~,~2\log_{}2)$$

p.109 練習5　\(a=2\) のとき、共有点 \((-1~,~-2)\)
　\(a=-2\) のとき、共有点 \((1~,~-2)\)

p.110 練習6\({\small (1)}~\)
　接線の方程式 \(y=-x+4\)
　法線の方程式 \(y=x-2\)
\({\small (2)}~\)
　接線の方程式 \(y=-2x+8\)
　法線の方程式 \(y={\large \frac{\,1\,}{\,2\,}}x+3\)

p.110 問1[証明] \(y^2=4px\) 上の点 \((x_1~,~y_1)\) より、$$~~~y_1^2=4px_1$$また、\(y^2=4px\) の両辺を \(x\) で微分すると、$$~~~2y\cdot y’=4p$$\(y\neq 0\) のとき、$$~~~y’=\frac{\,2p\,}{\,y\,}$$よって、傾きは \({\large \frac{\,2p\,}{\,y_1\,}}\) となり、\(y_1\neq 0\) での接線の方程式は、$$~~~y-y_1=\frac{\,2p\,}{\,y_1\,}(x-x_1)$$\(y_1^2=4px_1\) を代入すると、$$\begin{eqnarray}~~~y_1y-4px_1&=&2p(x+x_1)\\[2pt]~~~y_1y&=&2p(x+x_1)\end{eqnarray}$$また、\(y=0\) のとき接点が \((0~,~0)\) となり接線が \(x=0\)
これは \((x_1~,~y_1)=(0~,~0)\) のとき上の式を満たす
以上より、接線の方程式は \(y_1y=2p(x+x_1)\) [終]

p.110 練習7[証明] 楕円上の点 \((x_1~,~y_1)\) より、$$~~~\frac{\,{x_1}^2\,}{\,a^2\,}+\frac{\,{y_1}^2\,}{\,b^2\,}=1~~~\cdots{\large ①}$$また、両辺を \(x\) で微分すると、$$~~~\frac{\,2x\,}{\,a^2\,}+\frac{\,2y\,}{\,b^2\,}y’=0$$\(y\neq 0\) のとき、$$~~~y’=-\frac{\,b^2x\,}{\,a^2y\,}$$よって、接線の傾きは \(-{\large \frac{\,b^2x_1\,}{\,a^2y_1\,}}\) となるので \(y_1\neq 0\) での接線の方程式は、$$\begin{eqnarray}~~~y-y_1&=&-\frac{\,b^2x_1\,}{\,a^2y_1\,}(x-x_1)
\\[3pt]~~~\frac{\,b^2x_1\,}{\,a^2y_1\,}x+y&=&\frac{\,b^2x_1\,}{\,a^2y_1\,}x_1+y_1
\\[3pt]~~~\frac{\,x_1x\,}{\,a^2\,}+\frac{\,y_1y\,}{\,b^2\,}&=&\frac{\,{x_1}^2\,}{\,a^2\,}+\frac{\,{y_1}^2\,}{\,b^2\,}\end{eqnarray}$$①を代入すると、$$~~~\frac{\,x_1x\,}{\,a^2\,}+\frac{\,y_1y\,}{\,b^2\,}=1$$ここで、\(y_1=0\) のとき接点が \((\pm a~,~0)\) となり接線の方程式は \(x=\pm a\)
これは \((x_1~,~y_1)=(\pm a~,~0)\) のとき上の式を満たす
以上より、接線の方程式は$$~~~\frac{\,x_1x\,}{\,a^2\,}+\frac{\,y_1y\,}{\,b^2\,}=1$$[終]

p.113 練習8$${\small (1)}~c=1-\sqrt{3}$$$${\small (2)}~c=\log_{}(e-1)$$

p.113 練習9[証明] \(f(x)=e^x\) とおくと、\(f'(x)=e^x\)
\(f(x)\) はすべて実数 \(x\) で連続で微分可能であるから、平均値の定理より、$$~~~\frac{\,e^b-e^a\,}{\,b-a\,}=e^c~,~a< c < b$$これを満たす実数 \(c\) が存在する
ここで、\(f(x)\) は単調増加するので \(e^a< e^c < e^b\) となり、$$~~~e^a< \frac{\,e^b-e^a\,}{\,b-a\,} < e^b$$[終]

p.116 問2閉区間 \([a~,~b]\) において、\(a≦u < v≦b\) を満たす任意の \(u~,~v\) をとると、平均値の定理より、$$~~~f(v)-f(u)=(v-u)f'(c)~,~u< c< v$$これを満たす実数 \(c\) が存在する
 
２
[証明] \(v-u>0~,~f'(c)<0\) より、$$~~~f(v)-f(u)< 0$$これより、\(f(u)> f(v)\) であるので、閉区間 \([a~,~b]\) で単調減少 [終]
 
３
[証明] \(f'(c)=0\) より、$$\begin{eqnarray}~~~f(v)-f(u)&=&0\\[2pt]~~~f(u)&=&f(v)\end{eqnarray}$$\(a≦u < v≦b\) を満たす任意の \(u~,~v\) に対して \(f(u)=f(v)\) であるので、閉区間 \([a~,~b]\) で定数 [終]

p.116 問3[証明] \(a> 0\) で \(y=a^x\) はすべて実数で連続で微分可能であり、\(y’=a^x\log_{}a\)
\(a> 1\) のとき、\(y’> 0\) となるので、
\(a> 1\) のとき単調に増加する
 
また、\(0< a < 1\) のとき \(\log_{}a<0\) となり \(y'<0\) となる
\(0< a < 1\) のとき単調に減少する [終]

p.117 問4[証明] \(F(x)=g(x)-f(x)\) とすると、\(F'(x)=g'(x)-f'(x)\)
これより、区間 \((a~,~b)\) で常に \(g'(x)=f'(x)\) ならば \(F'(x)=0\)
したがって、\(F(x)\) は区間 \([a~,~b]\) で連続で \(C\) を定数として \(F(x)=C\)
よって、\(g(x)-f(x)=C\)
したがって、閉区間 \([a~,~b]\) で \(g(x)=f(x)+C\)、ただし \(C\) は定数 [終]

p.117 練習10\({\small (1)}~\)区間 \(0≦x≦2\pi\) で単調増加
\({\small (2)}~\)区間 \(0≦x\) で単調増加
　　区間 \(x≦0\) で単調減少
\({\small (3)}~\)区間 \(1≦x\) で単調増加
　　区間 \(0< x≦1\) で単調減少

p.119 練習11\({\small (1)}~\)
　\(x=1\) で極大値 \({\large \frac{\,1\,}{\,2\,}}\)
　\(x=-1\) で極小値 \(-{\large \frac{\,1\,}{\,2\,}}\)
\({\small (2)}~\)
　\(x={\large \frac{\,\pi\,}{\,2\,}}\) で極大値 \(3\)
　\(x={\large \frac{\,3\,}{\,2\,}}\pi\) で極小値 \(-1\)
\({\small (3)}~\)
　\(x={\large \frac{\,1\,}{\,\sqrt{e}\,}}\) で極小値 \(-{\large \frac{\,1\,}{\,2e\,}}\)
\({\small (4)}~\)
　\(x=1\) で極大値 \({\large \frac{\,1\,}{\,e\,}}\)

p.121 練習12\({\small (1)}~\)
　\(x=1\) で極大値 \(2\)
　\(x=3\) で極小値 \(0\)
\({\small (2)}~\)
　\(x=1\) で極大値 \(4\)
　\(x=0~,~2\) で極小値 \(3\)

p.121 練習13$$~~~a=-1$$

p.122 練習14\({\small (1)}~\)
　\(x=\sqrt{2}\) で最大値 \(2\)
　\(x=-\sqrt{2}\) で最小値 \(-2\)
\({\small (2)}~\)
　\(x={\large \frac{\,\pi\,}{\,2\,}}\) で最大値 \({\large \frac{\,\pi\,}{\,2\,}}\)
　\(x={\large \frac{\,3\,}{\,2\,}}\pi\) で最小値 \(-{\large \frac{\,3\,}{\,2\,}}\pi\)

p.123 練習15　\(\theta={\large \frac{\,\pi\,}{\,6\,}}\) のとき、最大値 \(3\sqrt{3}\)

p.126 練習16\({\small (1)}~\)
　\(x< -1~,~0< x\) で下に凸
　\(-1< x < 0\) で上に凸
　変曲点 \((-1~,~0)~,~(0~,~1)\)
\({\small (2)}~\)
　\(0< x < {\large \frac{\,\pi\,}{\,4\,}}~,~{\large \frac{\,3\,}{\,4\,}}\pi< x < \pi\) で上に凸
　\({\large \frac{\,\pi\,}{\,4\,}}< x < {\large \frac{\,3\,}{\,4\,}}\pi\) で下に凸
　変曲点 \(\left({\large \frac{\,\pi\,}{\,4\,}}~,~{\large \frac{\,\pi\,}{\,4\,}}\right)~,~\left({\large \frac{\,3\,}{\,4\,}}\pi~,~{\large \frac{\,3\,}{\,4\,}}\pi\right)\)
\({\small (3)}~\)
　\(x< -2\) で上に凸
　\(-2< x\) で下に凸
　変曲点 \((-2~,~-2e^{-2})\)

p.127 練習17\({\small (1)}~\)

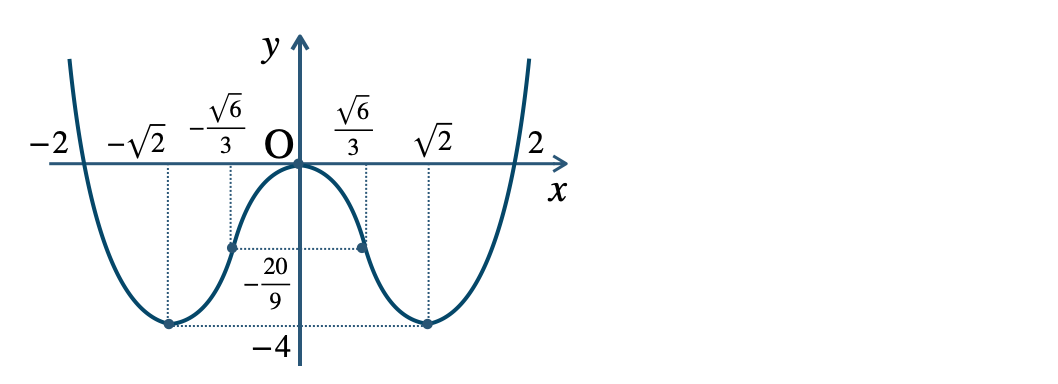
\({\small (2)}~\)

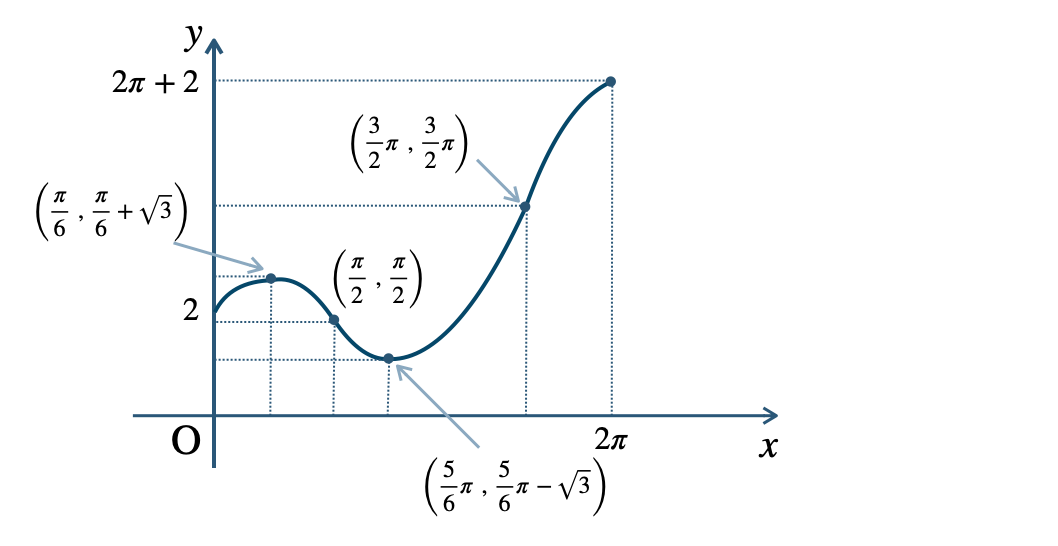
p.129 練習18\({\small (1)}~\)

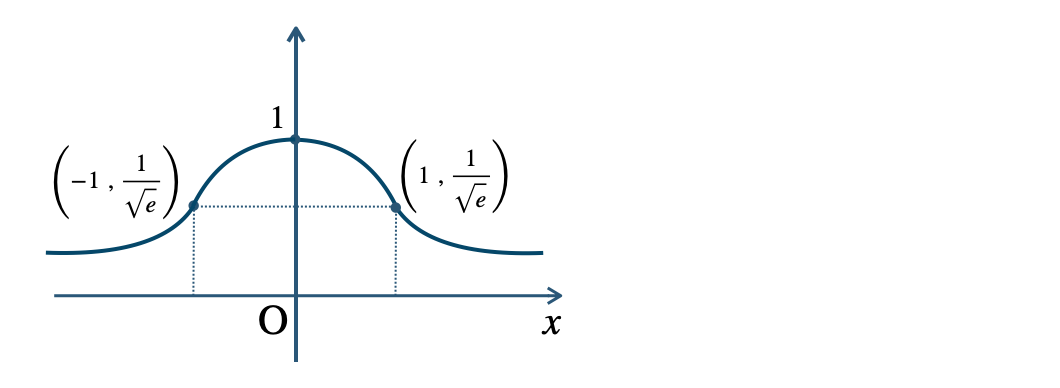
\({\small (2)}~\)

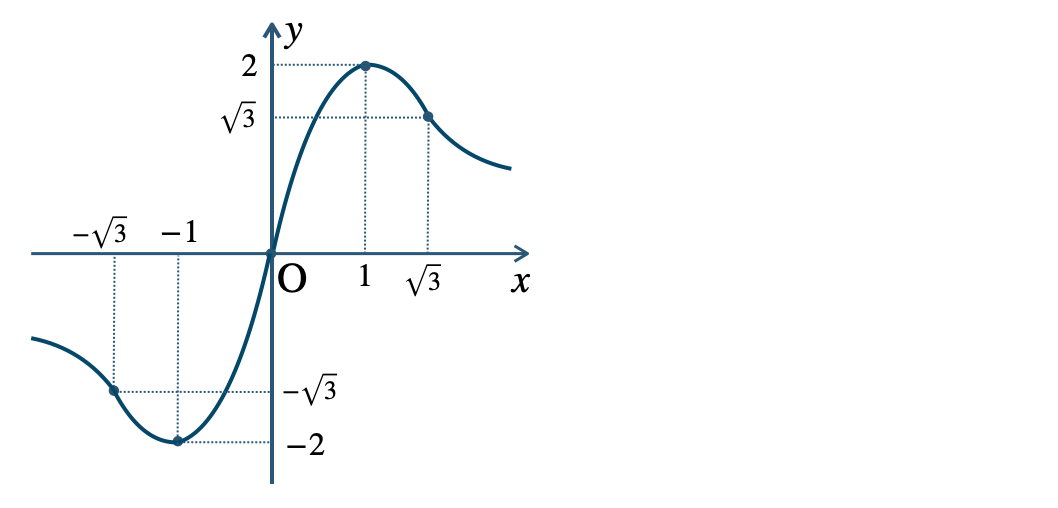
\({\small (3)}~\)

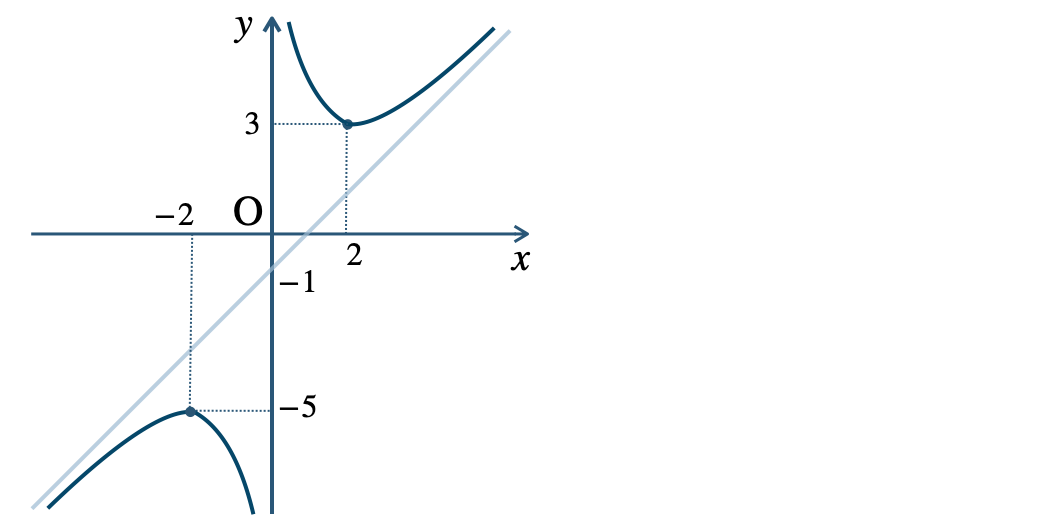
p.130 練習19\({\small (1)}~\)
　\(x=0\) で極大値 \(0\)
　\(x=-1\) で極小値 \(-5\)、\(x=2\) で極小値 \(-32\)
\({\small (2)}~\)
　\(x={\large \frac{\,\pi\,}{\,3\,}}\) で極大値 \({\large \frac{\,\sqrt{3}\,}{\,3\,}}\pi+1\)
　\(x={\large \frac{\,2\,}{\,3\,}}\pi\) で極小値 \({\large \frac{\,2\sqrt{3}\,}{\,3\,}}\pi-1\)

p.131 練習20[証明] \(f(x)=\log_{}(x+1)-x\) とすると、$$~~~f'(x)=\frac{\,1\,}{\,x+1\,}-1=-\frac{\,x\,}{\,x+1\,}$$\(x> 0\) のとき \(f'(x)< 0\) であるので、\(f(x)\) は \(x≧0\) で単調減少
また、\(f(0)=0\) であるので \(x> 0\) のとき \(f(x)< 0\)
したがって、\(x> 0\) で$$~~~\log_{}(x+1)< x$$[終]

p.131 問5[証明] \(f(x)=e^x-\left(1+x+{\large \frac{\,x^2\,}{\,2\,}}\right)\) とすると、$$~~~f'(x)=e^x-(1+x)$$例題10より \(f'(x)=e^x-(1+x)> 0\)
よって、\(f(x)\) は \(x≧0\) で単調増加
また、\(f(0)=0\) であるので \(x> 0\) のとき \(f(x)> 0\)
したがって、\(x> 0\) で$$~~~e^x > 1+x+\frac{\,x^2\,}{\,2\,}$$[終]

p.132 練習21\({\small (1)}~\)
　\(a< -1\) のとき、２個
　\(a=-1\) のとき、１個
　\(a> -1\) のとき、０個
\({\small (2)}~\)
　\(-{\large \frac{\,1\,}{\,e\,}} < a< 0\) のとき、２個
　\(a≧0~,~a=-{\large \frac{\,1\,}{\,e\,}}\) のとき、１個
　\(a< -{\large \frac{\,1\,}{\,e\,}}\) のとき、０個

p.133 問題 6[証明] \(f(x)=\log_{}(1+x)-x+{\large \frac{\,x^2\,}{\,2\,}}\) とすると、$$~~~f'(x)=\frac{\,1\,}{\,1+x\,}-1+x=\frac{\,x^2\,}{\,1+x\,}$$\(x> 0\) のとき \(f'(x)> 0\) であるので、\(f(x)\) は \(x≧0\) で単調増加
また、\(f(0)=0\) であるので \(x> 0\) のとき \(f(x)> 0\)
したがって、\(x> 0\) で$$~~~x-\frac{\,x^2\,}{\,2\,}< \log_{}(1+x)$$[終]

p.135 練習22　速度 \(v_0-gt~~[{\rm m/s}]\)
　加速度 \(-g~~[{\rm m/s^2}]\)

p.137 練習23\({\small (1)}~\)
　速さ \(3\sqrt{2}\)、加速度の大きさ \(2\)
\({\small (2)}~\)
　速さ \(2\pi\)、加速度の大きさ \(2\pi ^2\)

p.137 問6[証明] それぞれのベクトルの成分は、$$~~~\overrightarrow{v}=(-r\omega \sin{\omega t}~,~r\omega \cos{\omega t})$$$$~~~\overrightarrow{a}=(-r\omega ^2\cos{\omega t}~,~-r\omega ^2\sin{\omega t})$$これより、内積は$$\begin{split}&\overrightarrow{v}\cdot \overrightarrow{a}\\[2pt]~~=~&r^2\omega ^3\sin{\omega t}\cos{\omega t}\\[2pt]~~~~~~~~~~&-r^2\omega ^3\sin{\omega t}\cos{\omega t}\\[2pt]~~=~&0\end{split}$$したがって、\(\overrightarrow{v}\) と \(\overrightarrow{a}\) は垂直である [終]

p.138 練習24　\(t=1\) のとき、\(2\pi\)
　\(t=2\) のとき、\(0\)

p.139 問7[証明] \(f(x)=(1+x)^p\) とすると、$$~~~f'(x)=p(1+x)^{p-1}$$また、\(f(0)=1~,~f'(0)=p\)
よって、\(|x|\) が十分に小さいとき \(f(x)≒f(0)+f'(0)x\) が成り立つので、$$~~~(1+x)^p≒1+px$$[終]

p.139 練習25$${\small (1)}~\sqrt{1+x}≒1+\frac{\,1\,}{\,2\,}x$$$${\small (2)}~e^x≒1+x$$$${\small (3)}~\log_{10}(2+x)≒\log_{10}2+\frac{\,1\,}{\,2\log_{}10\,}x$$

p.140 練習26$${\small (1)}~10.025$$$${\small (2)}~1.992$$$${\small (3)}~0.485$$

p.142 演習問題Ａ 5\({\small (1)}~\)[証明] \(f(x)=\cos{x}-1+{\large \frac{\,x^2\,}{\,2\,}}\) とすると、$$~~~f'(x)=-\sin{x}+x$$$$~~~f”(x)=-\cos{x}+1$$\(f”(x)=0\) となるのは \(x=2\pi k\) ( \(k\) は整数 )のときで、それ以外では \(f”(x)> 0\)
よって、\(f'(x)\) は単調増加
また、\(f'(0)=0\) である
これより、\(x> 0\) のとき \(f'(x)> 0\) であるので、\(f(x)\) は \(x≧0\) で単調増加
また、\(f(0)=0\) であるので \(x> 0\) のとき \(f(x)> 0\)
したがって、\(x> 0\) で$$~~~\cos{x}> 1-\frac{\,x^2\,}{\,2\,}$$[終]
 
\({\small (2)}~\)[証明] \(f(x)=\sin{x}-x+{\large \frac{\,x^3\,}{\,6\,}}\) とすると、$$~~~f'(x)=\cos{x}-1+\frac{\,x^2\,}{\,2\,}$$\(x> 0\) のとき \(f'(x)> 0\) であるので、\(f(x)\) は \(x≧0\) で単調増加
また、\(f(0)=0\) であるので \(x> 0\) のとき \(f(x)> 0\)
したがって、\(x> 0\) で$$~~~\sin{x} > x-\frac{\,x^3\,}{\,6\,}$$[終]

p.143 演習問題Ｂ 11[証明]$$~~~f'(x)=3x^2+6ax+3b$$$$~~~f'{}'(x)=6x+6a$$\(f'{}'(x)=0\) より、\(x=-a\)
よって、変曲点Ａは \((-a~,~2a^3-3ab+c)\)
ここで、Ｃのグラフを点Ａが原点に重なるように平行移動させるとそのグラフは、$$~~~g(x)=x^3+3(b-a^2)x$$ここで、$$~~~g(-x)=-x^3-3(b-a^2)x=-g(x)$$となるので、\(g(x)\) は原点に関して対称である
したがって、曲線Ｃ上にＡ以外の任意の点Ｐをとり、Ａに関して対称な点をＱとすると、Qも曲線Ｃ上にある [終]

p.143 演習問題Ｂ 13[証明] \(t\) 秒後の水の深さを \(h~[{\rm cm}]\)、水の量を \(V~[{\rm cm}^3]\) とすると、
\(h=\sqrt[\large 3]{V^2}\) より、\(V=h^{{\large \frac{\,3\,}{\,2\,}}}\)
両辺を \(t\) で微分すると、$$~~~\frac{\,dV\,}{\,dt\,}=\frac{\,3\,}{\,2\,}h^{\frac{\,1\,}{\,2\,}}\frac{\,dh\,}{\,dt\,}$$水を入れる量は一定より、\({\large \frac{\,dV\,}{\,dt\,}}\) が一定
これより、水の深さの正の平方根 \(h^{{\large \frac{\,1\,}{\,2\,}}}\) と水面の上昇する速度 \({\large \frac{\,dh\,}{\,dt\,}}\) の積が一定である
したがって、水面の上昇する速度は、水の深さの正の平方根に反比例する [終]