今回の問題は「不等式を満たす整数の解」です。
問題次の問いに答えよ。
\({\small (1)}~\)次の不等式を満たす最小の整数 \(x\) を求めよ。$$~~~12(x-3)>2x+9$$\({\small (2)}~\)次の不等式を満たす最大の整数 \(x\) を求めよ。$$~~~\frac{x+1}{5}>\frac{x+3}{2}$$
\({\small (1)}~\)次の不等式を満たす最小の整数 \(x\) を求めよ。$$~~~12(x-3)>2x+9$$\({\small (2)}~\)次の不等式を満たす最大の整数 \(x\) を求めよ。$$~~~\frac{x+1}{5}>\frac{x+3}{2}$$
Point:不等式を満たす整数の解不等式を満たす整数の解の求め方は、
① 与えられた不等式の解を求める。
② 解の範囲を数直線上に表す。
③ 範囲を満たす整数解を目で見て読み取る。
例えば、\(1< x≦{\Large \frac{\,7\,}{\,2\,}}\)を満たす整数解すべては、

また、\(x<{\Large \frac{\,8\,}{\,3\,}}\) を満たす最大の整数は、

① 与えられた不等式の解を求める。
② 解の範囲を数直線上に表す。
③ 範囲を満たす整数解を目で見て読み取る。
例えば、\(1< x≦{\Large \frac{\,7\,}{\,2\,}}\)を満たす整数解すべては、
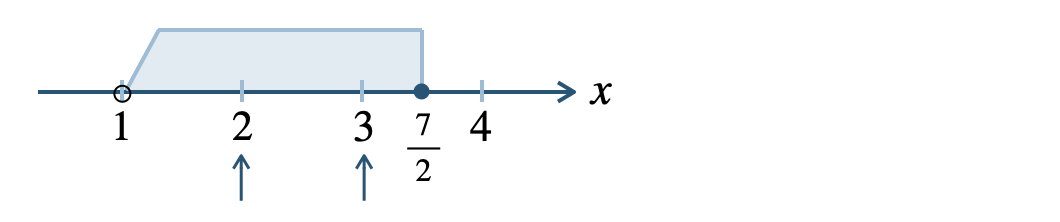
数直線より、答えは \(x=2~,~3\) となる
※ \(x=1\) は含まない
また、\(x<{\Large \frac{\,8\,}{\,3\,}}\) を満たす最大の整数は、
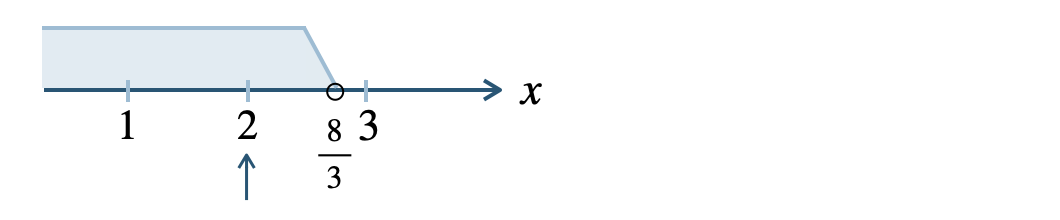
数直線より、答えは \(x=2\) となる
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
次のページ「解法のPointと問題解説」


