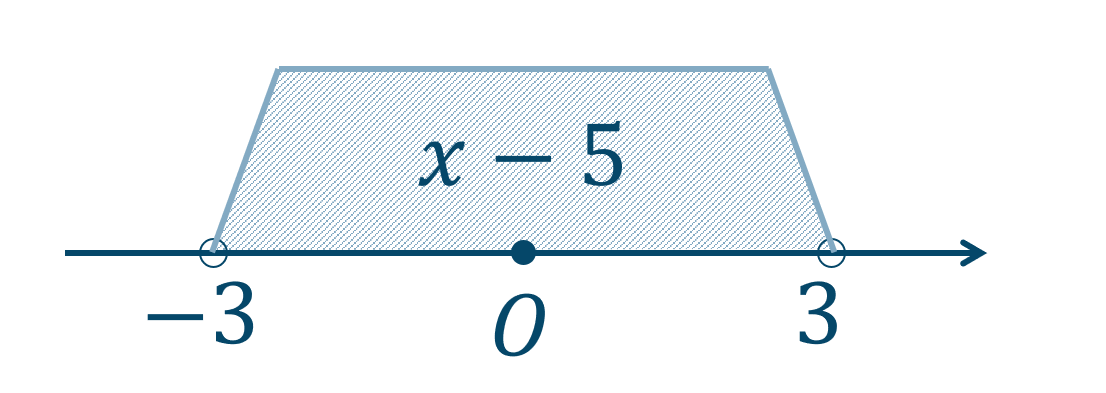絶対値を含む方程式と不等式の解法
\(a\) を正の定数として、( ※ 右辺が定数 )
\({\small (1)}~\begin{split}|\,x\,|=a~\Leftrightarrow~x=\pm\, a\end{split}\)
※ 原点からの距離が \(a\) となる点が解となる。

\({\small (2)}~\begin{split}|\,x\,|<a~\Leftrightarrow~-a<x<a\end{split}\)
※ 原点からの距離が \(a\) よりも小さくなればよい。

\({\small (3)}~\begin{split}|\,x\,|>a~\Leftrightarrow~x<-a~,~a<x\end{split}\)
※ 原点からの距離が \(a\) よりも大きくなればよい。

※ これらは絶対値の中が \(x\) の式でも使える。
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
問題解説:絶対値を含む方程式と不等式
問題解説(1)
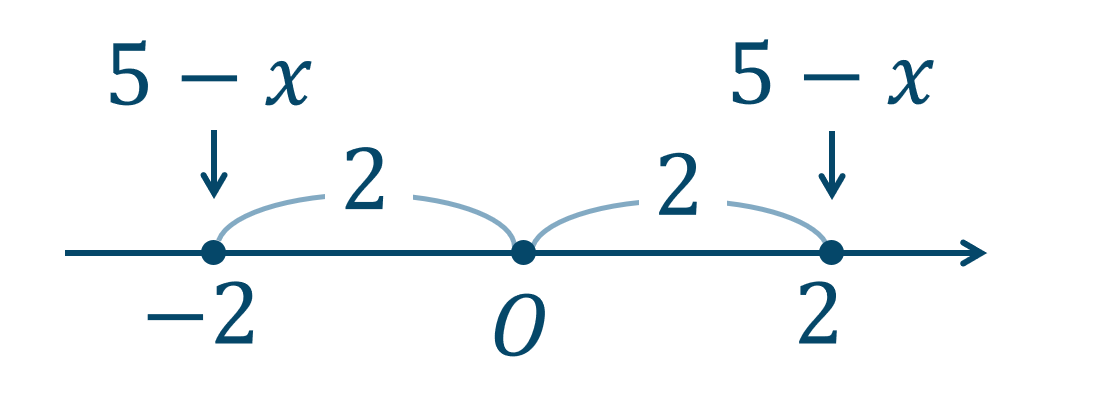
\(x\) の式 \(5-x\) と原点からの距離が \(2\) となればよいので、
絶対値を外すと、$$~~~5-x=\pm 2$$
(ⅰ) \( 5-x=2 \) のとき、$$~~~5-x=2$$\(5\) を右辺に移項すると、$$~~~-x=2-5$$$$~~~-x=-3$$\(-1\) を両辺にかけると、$$~~~~~~~x=3$$
(ⅱ) \( 5-x=-2 \) のとき、$$~~~5-x=-2$$\(3\) を右辺に移項すると、$$~~~-x=-2-5$$$$~~~-x=-7$$\(-1\) を両辺にかけると、$$~~~~~~~x=7$$
(ⅰ)と(ⅱ)より、答えは \(x=3~,~7\) となります。
問題解説(2)
\(x\) の式 \(x-5\) と原点からの距離が \(3\) より小さくなればよいので、数直線上に表すと次のようになります。
よって、式は \(-3<x-5<3\) となるのでこれを解くと、$$~~~-3<x-5<3$$各辺に \(5\) を加えると、$$~-3+5<x-5+5<3+5$$$$~~~~~~~~2<x<8$$よって、答えは \(2<x<8\) となります。
問題解説(3)
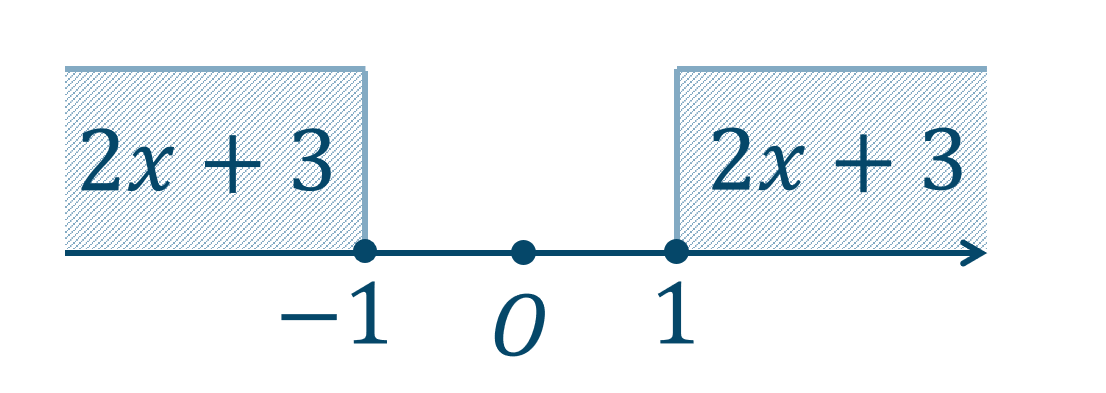
\(x\) の式 \(2x+3\) と原点からの距離が \(1\) 以上になればよいので、数直線上に表すと次のようになります。
よって、式は \(2x+3≦-1~,~1≦2x+3\) となるのでこれを解くと、
左の式は、$$~~~2x+3≦-1$$\(3\) を右辺に移項すると、$$~~~2x≦-1-3$$$$~~~2x≦-4$$両辺を \(2\) で割ると、不等号の向きはそのままなので、$$~~~~x≦-2$$
右の式は、$$~~~~~1≦2x+3$$\(1\) を右辺に、\(2x\) を左辺に移項すると、$$~-2x≦3-1$$$$~-2x≦2$$両辺を \(-2\) で割ると、不等号の向きは逆になるので、$$~~~~~~x≧-1$$よって、答えは \(x≦-2~,~-1≦x\) となります。
今回のまとめ
絶対値をを含む式の解法はこの数直線を書いて、視覚的に解くのが基本となります。まずこのパターンを覚えて解けるようになりましょう!