今回の問題は「補集合とド・モルガンの法則」です。
問題全体集合 \(\rm U\) が1~10までの自然数であり、この全体集合の部分集合で要素が3の倍数の集合を \(\rm A\)、要素が素数の集合を \(\rm B\) とするとき、次の集合を要素を書き並べる方法で表せ。$${\small (1)}~\overline {\rm A}$$$${\small (2)}~\overline {{\rm A} \cup {\rm B}}$$$${\small (3)}~\overline {{\rm A}} \cup \overline {{\rm B}}$$$${\small (4)}~\overline {{\rm A}} \cap \overline {{\rm B}}$$$${\small (5)}~\overline {{\rm A}} \cap {\rm B}$$$${\small (6)}~{\rm A} \cup \overline {{\rm B}}$$
Point:全体集合と補集合ある1つの集合 \({\rm U}\) の部分集合だけを考えるとき、
この集合 \({\rm U}\) を「全体集合」という。
このとき、集合 \({\rm A}\) に属さない要素の集合を、
集合 \({\rm A}\) の補集合 \({\rm \overline {\,A\,}}\)

■ 補集合の公式
\({\small (1)}~~{\rm A}\cap \overline {{\rm A}}=\phi \)
※ 集合とその補集合の共通部分は空集合。
\({\small (2)}~~{\rm A}\cup \overline {{\rm A}}={\rm U} \)
※ 集合とその補集合の和集合は全体集合。
\({\small (3)}~~\overline {\overline {{\rm A}}}={\rm A}\) ※ 補集合の補集合
\({\small (4)}~~\overline {{\rm U}}=\phi \) ※ 全体集合の補集合
\({\small (5)}~~\overline {\phi}={\rm U} \) ※ 空集合の補集合
この集合 \({\rm U}\) を「全体集合」という。
このとき、集合 \({\rm A}\) に属さない要素の集合を、
集合 \({\rm A}\) の補集合 \({\rm \overline {\,A\,}}\)

■ 補集合の公式
\({\small (1)}~~{\rm A}\cap \overline {{\rm A}}=\phi \)
※ 集合とその補集合の共通部分は空集合。
\({\small (2)}~~{\rm A}\cup \overline {{\rm A}}={\rm U} \)
※ 集合とその補集合の和集合は全体集合。
\({\small (3)}~~\overline {\overline {{\rm A}}}={\rm A}\) ※ 補集合の補集合
\({\small (4)}~~\overline {{\rm U}}=\phi \) ※ 全体集合の補集合
\({\small (5)}~~\overline {\phi}={\rm U} \) ※ 空集合の補集合
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
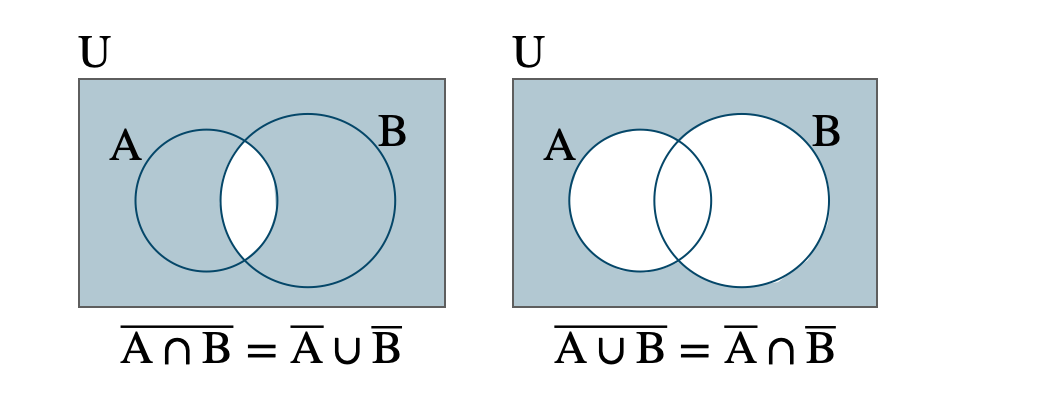
Point:ド・モルガンの法則
共通部分の補集合 \(\begin{eqnarray}{\rm \overline {\,A\cap B\,}}&=&{\rm \overline {\,A\,}}\cup{\rm \overline {\,B\,}}\end{eqnarray}\)
和集合の補集合 \(\begin{eqnarray}{\rm \overline {\,A\cup B\,}}&=&{\rm \overline {\,A\,}}\cap{\rm \overline {\,B\,}}\end{eqnarray}\)

■ 集合の演算の手順
① 全体集合とその部分集合のベン図にかく。
② 補集合、和集合や共通部分をベン図で確認して、要素を求める。
③ わかりにくい集合の場合は、ド・モルガンの法則を利用して簡単な集合で表す。
■ ド・モルガンの法則
全体集合 \({\rm U}\) とその部分集合 \({\rm A~,~B}\) について、
共通部分の補集合 \(\begin{eqnarray}{\rm \overline {\,A\cap B\,}}&=&{\rm \overline {\,A\,}}\cup{\rm \overline {\,B\,}}\end{eqnarray}\)
和集合の補集合 \(\begin{eqnarray}{\rm \overline {\,A\cup B\,}}&=&{\rm \overline {\,A\,}}\cap{\rm \overline {\,B\,}}\end{eqnarray}\)
■ 集合の演算の手順
① 全体集合とその部分集合のベン図にかく。
② 補集合、和集合や共通部分をベン図で確認して、要素を求める。
③ わかりにくい集合の場合は、ド・モルガンの法則を利用して簡単な集合で表す。
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
次のページ「解法のPointと問題解説」


