補集合とド・モルガンの法則の解法
この集合 \({\rm U}\) を「全体集合」という。
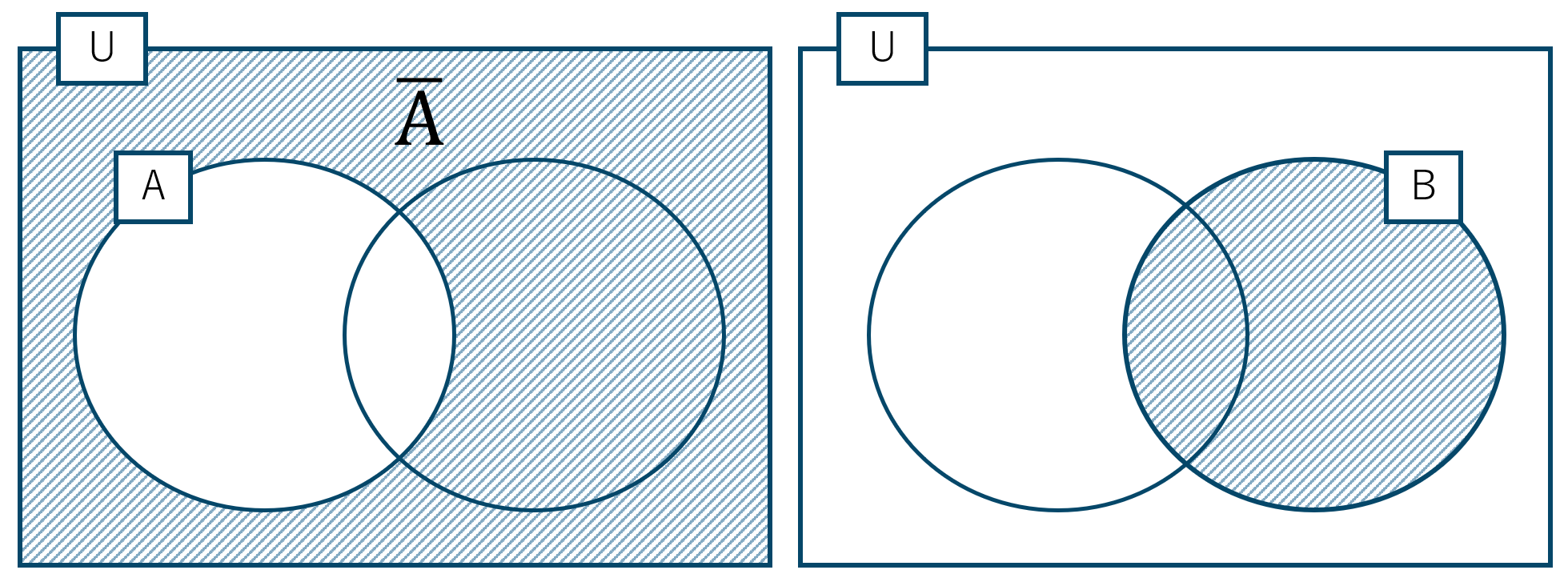
このとき、集合 \({\rm A}\) に属さない要素の集合を、
集合 \({\rm A}\) の補集合 \({\rm \overline {\,A\,}}\)

■ 補集合の公式
\({\small (1)}~~{\rm A}\cap \overline {{\rm A}}=\phi \)
※ 集合とその補集合の共通部分は空集合。
\({\small (2)}~~{\rm A}\cup \overline {{\rm A}}={\rm U} \)
※ 集合とその補集合の和集合は全体集合。
\({\small (3)}~~\overline {\overline {{\rm A}}}={\rm A}\) ※ 補集合の補集合
\({\small (4)}~~\overline {{\rm U}}=\phi \) ※ 全体集合の補集合
\({\small (5)}~~\overline {\phi}={\rm U} \) ※ 空集合の補集合
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
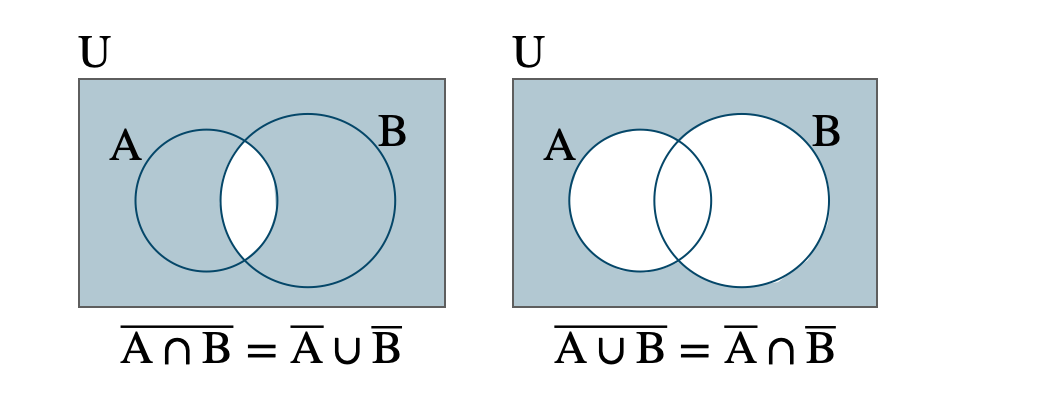
■ ド・モルガンの法則
全体集合 \({\rm U}\) とその部分集合 \({\rm A~,~B}\) について、
共通部分の補集合 \(\begin{eqnarray}{\rm \overline {\,A\cap B\,}}&=&{\rm \overline {\,A\,}}\cup{\rm \overline {\,B\,}}\end{eqnarray}\)
和集合の補集合 \(\begin{eqnarray}{\rm \overline {\,A\cup B\,}}&=&{\rm \overline {\,A\,}}\cap{\rm \overline {\,B\,}}\end{eqnarray}\)
■ 集合の演算の手順
① 全体集合とその部分集合のベン図にかく。
② 補集合、和集合や共通部分をベン図で確認して、要素を求める。
③ わかりにくい集合の場合は、ド・モルガンの法則を利用して簡単な集合で表す。
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
問題解説:補集合とド・モルガンの法則
問題解説(1)
全体集合 \(\rm U\) は、$$~~~{\rm U}=\{~1~,~2~,~3~,~4~,~5~,~6~,~7~,~8~,~9~,~10~\}$$集合 \(\rm A\) は、$$~~~{\rm A}=\{~3~,~6~,~9~\}$$集合 \(\rm B\) は、$$~~~{\rm B}=\{~2~,~3~,~5~,~7~\}$$
よって、集合 \( \overline {\rm A} \)は、\(\rm A\) に属さない集合 \(\rm U\) の要素であることより、$$~~~\overline {\rm A}=\{~1~,~2~,~4~,~5~,~7~,~8~,~10~\}$$
問題解説(2)
\({\rm A} \cup {\rm B}\) は集合 \(\rm A\) と集合 \(\rm B\) の和集合で、$$~~~{\rm A}=\{~3~,~6~,~9~\}$$$$~~~{\rm B}=\{~2~,~3~,~5~,~7~\}$$よって、集合 \(\rm A\) と集合 \(\rm B\) の少なくとも一方に属していればよいので、$$~~~{\rm A} \cup {\rm B}=\{~2~,~3~,~5~,~6~,~7~,~9~\}$$
よって、\( \overline {{\rm A} \cup {\rm B}} \)は集合 \({\rm A} \cup {\rm B}\) に属さない集合 \(\rm U\) の要素より、$$~~~\overline {{\rm A} \cup {\rm B}}=\{~1~,~4~,~8~,~10~\}$$
問題解説(3)
ド・モルガンの法則より、$$\overline {{\rm A}} \cup \overline {{\rm B}}=\overline {{\rm A} \cap {\rm B}}$$ここで、\( {\rm A} \cap {\rm B} \) は集合 \(\rm A\) と集合 \(\rm B\) の共通部分で、$$~~~{\rm A}=\{~3~,~6~,~9~\}$$$$~~~{\rm B}=\{~2~,~3~,~5~,~7~\}$$よって、これらに共通して属しているので、$$~~~{\rm A} \cap {\rm B}=\{~3~\}$$
よって、\( \overline {{\rm A} \cap {\rm B}} \) は \({\rm A} \cap {\rm B}\) に属さない集合 \(\rm U\) の要素より、$$~~~\overline {{\rm A} \cap {\rm B}}=\{~1~,~2~,~4~,~5~,~6~,~7~,~8~,~9~,~10~\}$$よって、答えは$$~~~\overline {{\rm A}} \cup \overline {{\rm B}}=\{~1~,~2~,~4~,~5~,~6~,~7~,~8~,~9~,~10~\}$$となります。
問題解説(4)
ド・モルガンの法則より$$\overline {{\rm A}} \cap \overline {{\rm B}}=\overline {{\rm A} \cup {\rm B}}$$(2)の答えより、$$~~~\overline {{\rm A} \cup {\rm B}}=\{~1~,~4~,~8~,~10~\}$$したがって、答えは$$~~~\overline {{\rm A}} \cap \overline {{\rm B}}=\{~1~,~4~,~8~,~10~\}$$となります。
問題解説(5)
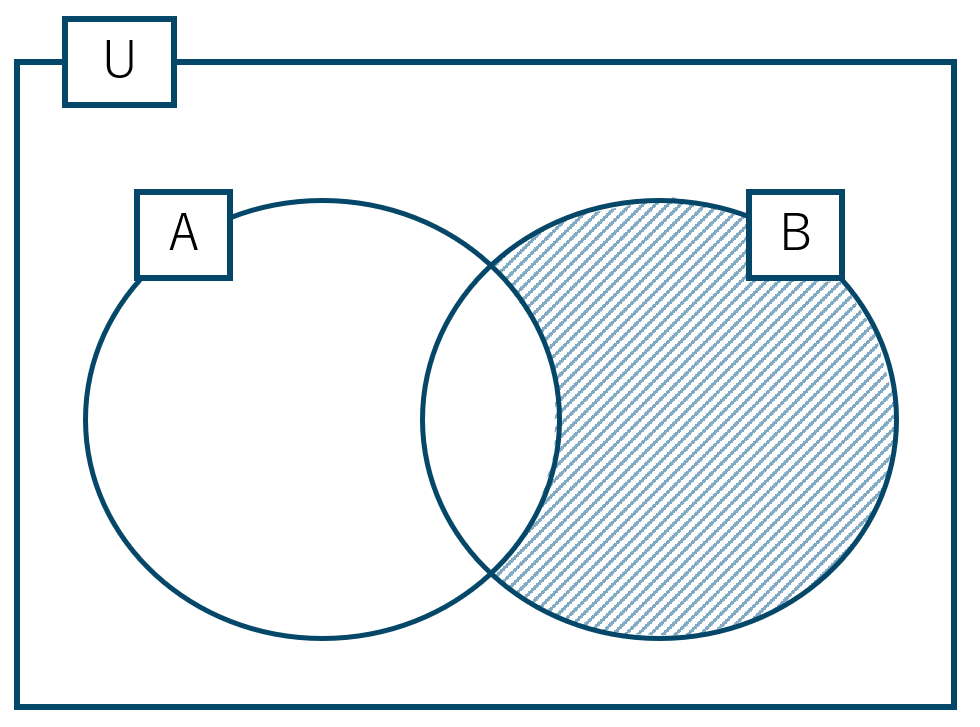
\( \overline {{\rm A}} \cap {\rm B} \) は次のベン図の共通部分となります。
この共通部分は次のようになります。
よって、集合 \(\rm B\) に属して集合 \( {\rm A} \cap {\rm B} \) に属さない要素となるので、$$~~~{\rm B}=\{~2~,~3~,~5~,~7~\}$$$$~~~{\rm A} \cap {\rm B}=\{~3~\}$$よって、答えは$$~~~\overline {{\rm A}} \cap {\rm B}=\{~2~,~5~,~7~\}$$となります。
問題解説(6)
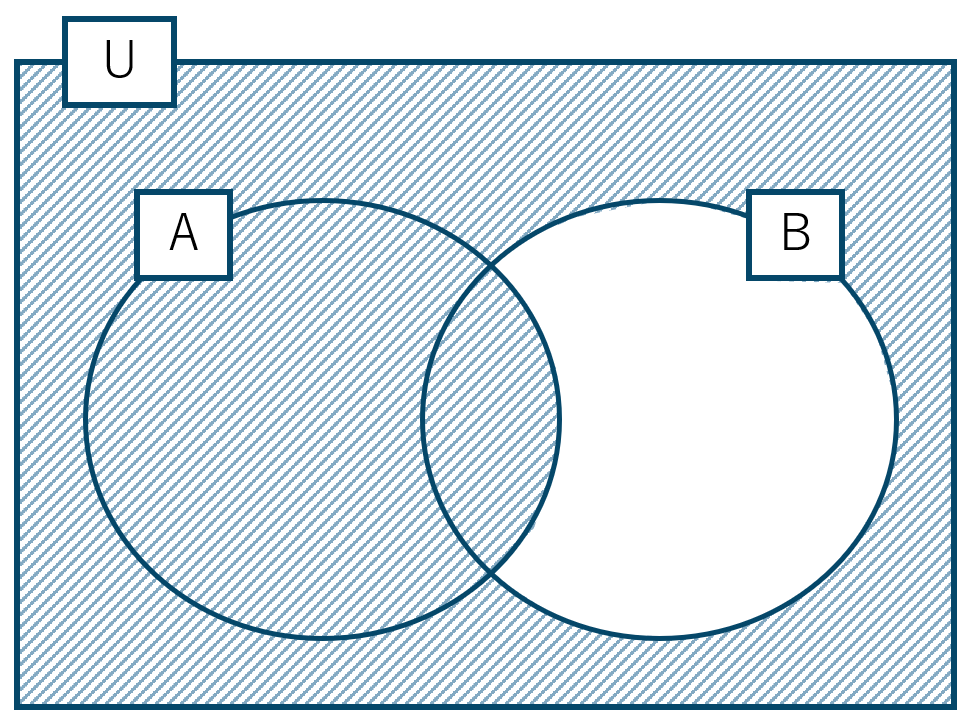
\( {\rm A} \cup \overline {{\rm B}} \) は次のベン図の斜線部分となります。
これは、集合 \( \overline {{\rm A}} \cap {\rm B} \) の補集合となるので、(5)の答えより、$$~~~\overline {{\rm A}} \cap {\rm B}=\{~2~,~5~,~7~\}$$
よって、\( {\rm A} \cup \overline {{\rm B}} \) は \( \overline {{\rm A}} \cap {\rm B} \) に属さない集合 \(\rm U\) の要素より、答えは$$~~~{\rm A} \cup \overline {{\rm B}}=\{~1~,~3~,~4~,~6~,~8~,~9~,~10~\}$$となります。
今回のまとめ
補集合とド・モルガンの法則は考え方も合わせて覚えておきましょう。また、複雑な集合の要素はベン図を描いて視覚的に解けるようにしましょう。