数直線と集合の解法
例えば、
\({\rm A}=\{~x~|~-1< x≦2~\}\)
\({\rm B}=\{~x~|~x≧1~\}\)
\({\small (1)}~\)補集合 \({\rm \overline {\,A\,}}\) は、\({\rm A}\) に属さない要素の範囲
よって、\({\rm \overline {\,A\,}}=\{~x~|~x≦-1~,~2< x~\}\)

\({\small (2)}~\)共通部分 \({\rm A\cap B}\) は、
どちらにも属する要素の範囲
よって、\({\rm A\cap B}=\{~x~|~1≦x≦2~\}\)

\({\small (3)}~\)和集合 \({\rm A\cup B}\) は、
少なくとも一方に属する要素の範囲
よって、\({\rm A\cup B}=\{~x~|~x> -1~\}\)

©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
問題解説:数直線と集合
問題解説(1)
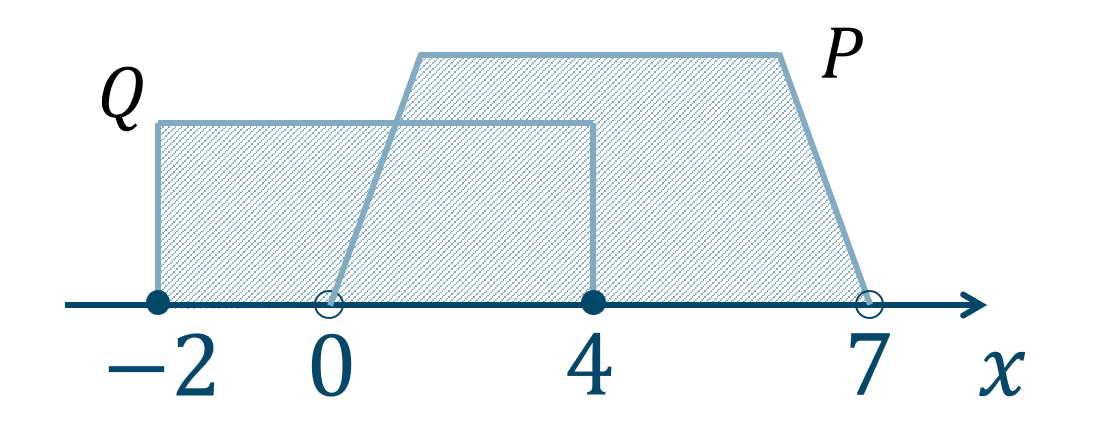
数直線上に範囲を表すと、
\({\rm P}\) と \({\rm Q}\) の少なくとも一方の範囲に含まれていればよいので、答えは$$~~~{\rm P}\cup {\rm Q}=\{~x~|~-2≦x<7~\}$$となります。
問題解説(2)
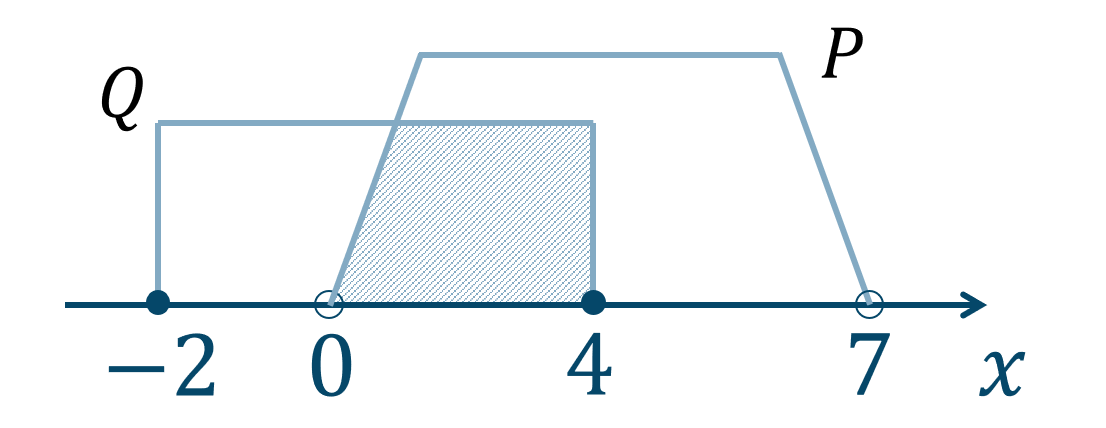
数直線上に範囲を表すと、
\({\rm P}\) と \({\rm Q}\) のどちらにも含まれる範囲であればよいので、答えは$$~~~{\rm P}\cap {\rm Q}=\{~x~|~0<x≦4~\}$$となります。
問題解説(3)
\(\overline{{\rm P}}\) は \({\rm P}\) の補集合より$$~~~\overline{{\rm P}}=\{~x~|~x≦0~,~7≦x~\}$$よって、\(\overline{{\rm P}}\cup {\rm Q}\) を数直線上に範囲を表すと、
\(\overline{{\rm P}}\)と \({\rm Q}\) の少なくとも一方に含まれていればよいので、答えは$$~~~\overline{{\rm P}}\cup {\rm Q}=\{~x~|~x≦4~,~7≦x~\}$$となります。
問題解説(4)
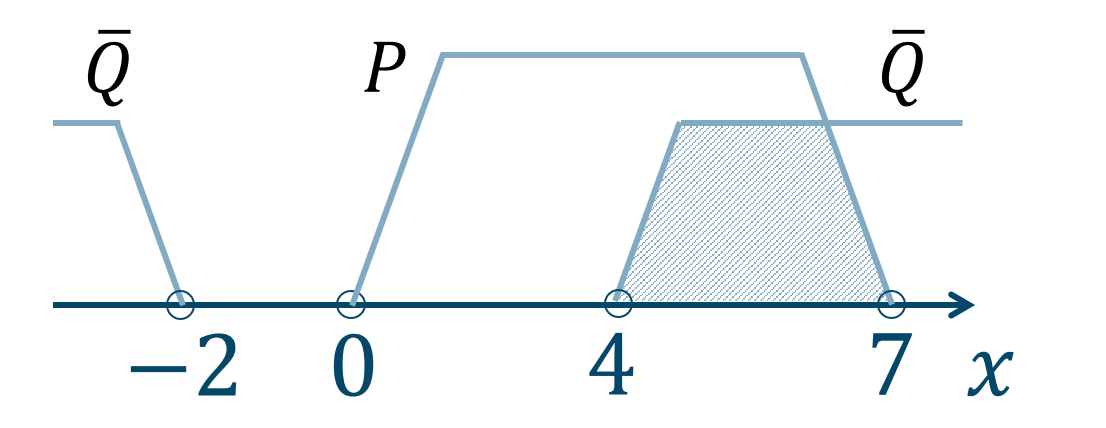
\(\overline{{\rm Q}}\) は \({\rm Q}\) の補集合であるので、$$~~~\overline{{\rm Q}}=\{~x~|~x<-2~,~4<x~\}$$よって、\({\rm P}\cap \overline{{\rm Q}}\) を数直線上に範囲を表すと、
\({\rm P}\) と \(\overline{{\rm Q}}\) のどちらにも含まれる範囲であればよいので、答えは$$~~~{\rm P}\cap \overline{{\rm Q}}=\{~x~|~4<x<7~\}$$となります。
今回のまとめ
数直線の集合でも視覚的に解くのが基本となります。それぞれの集合の範囲を数直線に書き込んで視覚的に解いていきましょう。