命題の真偽

2018.04.212024.02.18

命題の真偽の解法

Point：命題と条件の真偽■ 命題と条件正しいか正しくないかの判定ができる事柄を表す式や文を「命題」という。
　正しいときは「真」である
　正しくないときは「偽」である

　(例) \(\sqrt{3}\) は無理数である→真

命題の中で変数 \(x\) を含み、その変数 \(x\) の値によって真偽が変わるものを「条件」という。

　(例) \(x\) は無理数である
　　　\(x=\sqrt{3}\) のとき→真、\(x=3\) のとき→偽

■ 仮定と結論
命題を２つの条件 \(p\) (仮定)と \(q\) (結論)を用いて、

\(p~\Rightarrow~q\)　「\(p\) ならば \(q\)」

\({\small (1)}~\)\(p~\Rightarrow~q\) が真のとき、

　　すべての \(p\) が \(q\) も成り立つ

\({\small (2)}~\)\(p~\Rightarrow~q\) が偽のとき、

　　\(p\) を満たすが \(q\) を満たさないものがある
　　→ このときの例を「反例」という

©︎ 2024 教科書より詳しい高校数学 yorikuwa.com

問題次の命題の真偽を答えよ。
\({\small (1)}~\)２つの三角形が合同ならば、それらは面積が等しい

\(p\)：２つの三角形が合同
\(q\)：２つの三角形の面積が等しい

\(p~\Rightarrow~q\) を考えると、
どんな２つの三角形でも合同ならば面積は等しくなります。
よって、答えは真となります。

問題次の命題の真偽を答えよ。
\({\small (2)}~\)ある四角形がひし形ならば、その四角形は平行四辺形である

\(p\)：ある四角形がひし形
\(q\)：ある四角形は平行四辺形

\(p~\Rightarrow~q\) を考えると、
平行四辺形の分類図が次のようになるので、

どんなひし形でも平行四辺形となります。
よって、答えは真となります。

問題次の命題の真偽を答えよ。
\({\small (3)}~\)２つの長方形の面積が等しいならば、それらは合同である

\(p\)：２つの長方形の面積が等しい
\(q\)：２つの長方形が合同である

\(p~\Rightarrow~q\) を考えると、
面積が等しい２つの長方形で合同でないものもあります。
例えば、

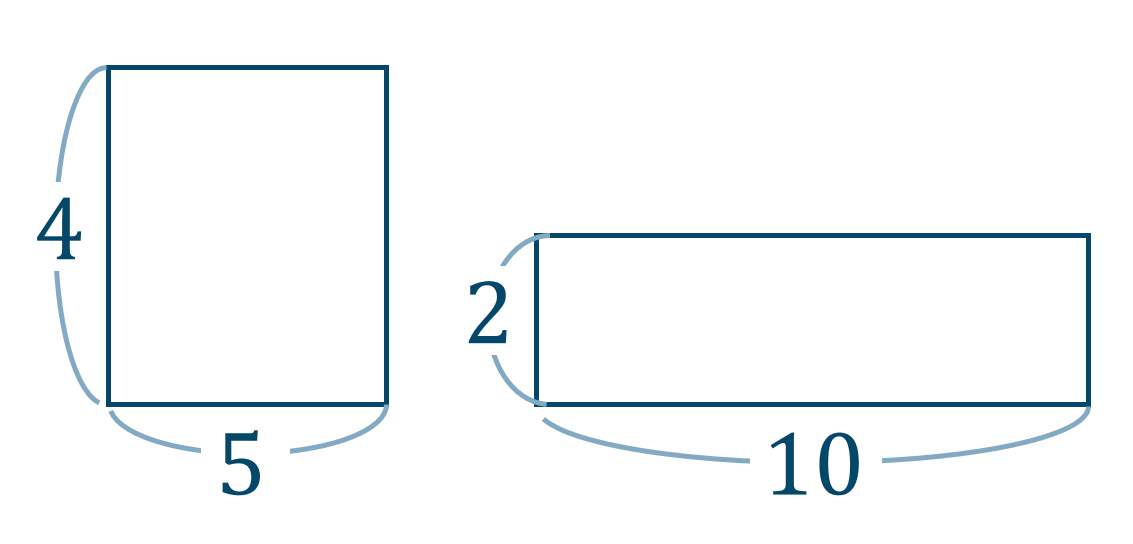
よって、答えは偽となります。

問題次の命題の真偽を答えよ。
\({\small (4)}~\)ある四角形が長方形ならば、その四角形は正方形である

\(p\)：ある四角形が長方形
\(q\)：ある四角形が正方形

\(p~\Rightarrow~q\) を考えると、
平行四辺形の分類図が次のようになるので、

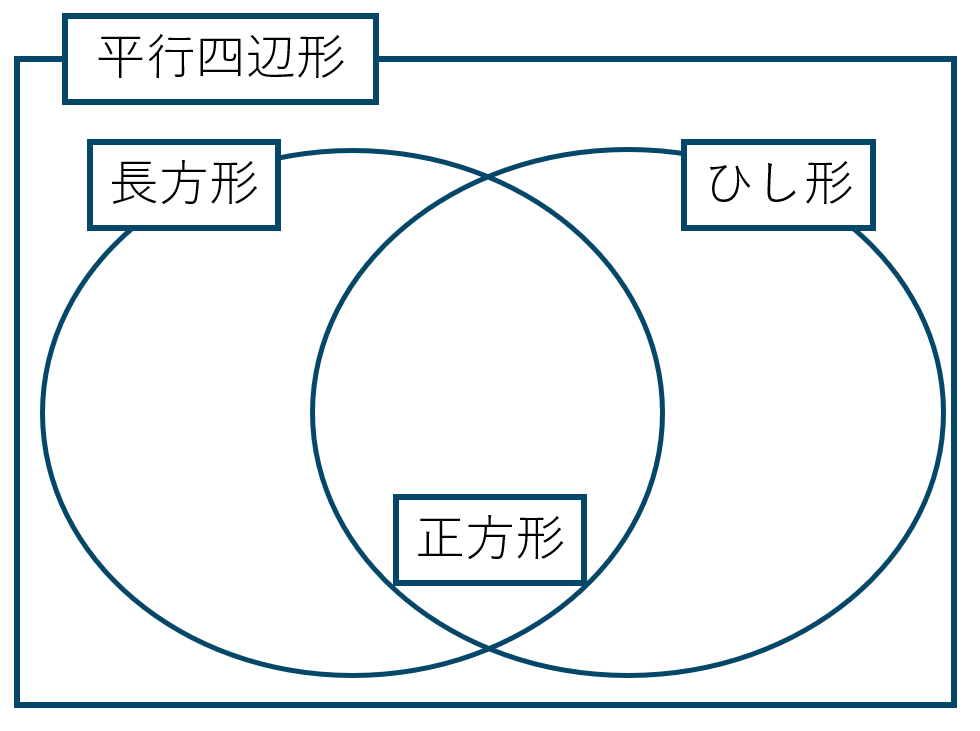
長方形であっても、必ず正方形になるとは限りません。
よって、答えは偽となります。

真偽の判定方法は「どんな \(p\) でも必ず \(q\) が成り立つか」を考えることです。また、平行四辺形の分類などの知識も覚えておきましょう。