条件の真偽の解法
正しいときは「真」である
正しくないときは「偽」である
(例) \(\sqrt{3}\) は無理数である→真
命題の中で変数 \(x\) を含み、その変数 \(x\) の値によって真偽が変わるものを「条件」という。
(例) \(x\) は無理数である
\(x=\sqrt{3}\) のとき→真、\(x=3\) のとき→偽
■ 仮定と結論
命題を2つの条件 \(p\) (仮定)と \(q\) (結論)を用いて、
\(p~\Rightarrow~q\) 「\(p\) ならば \(q\)」
\({\small (1)}~\)\(p~\Rightarrow~q\) が真のとき、
すべての \(p\) が \(q\) も成り立つ
\({\small (2)}~\)\(p~\Rightarrow~q\) が偽のとき、
\(p\) を満たすが \(q\) を満たさないものがある
→ このときの例を「反例」という
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
命題「\(p~\Rightarrow~q\)」の真偽を判断するとき、
条件 \(p\) を満たす \(x\) の集合を \({\rm P}\)
条件 \(q\) を満たす \(x\) の集合を \({\rm Q}\)
とすると、
\({\rm P}\) が \({\rm Q}\) の部分集合 \({\rm P\subset Q}\) であれば真
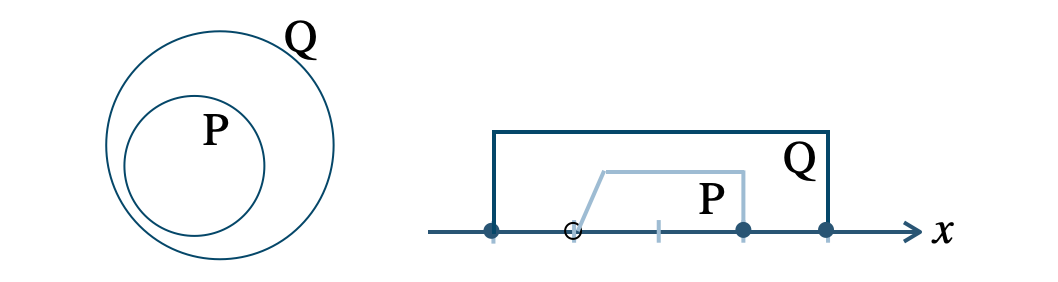
※ \({\rm Q}\) にならない \({\rm P}\) の要素 \(x\) な存在するならば、これが反例となり偽となる。
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
問題解説:条件の真偽
問題解説(1)
\({\small (1)}~ab>0\) ならば \(a>0\) かつ \(b>0\)
\(p\):\(ab>0\)
\(q\):\(a>0\) かつ \(b>0\)
\(p~\Rightarrow~q\) を考えると、
\(a=-1~,~b=-2\) のとき、
\(p\) は$$~~~ab=(-1)\cdot(-2)=2>0$$より満たすが、\(q\) は、$$~~~a=-1<0~,~b=-2<0$$となり満たさない。
よって、答えは偽となります。また、反例の1つは、\(a=-1~,~b=-2\) のときとなります。
問題解説(2)
\({\small (2)}~a=1\) かつ \(b=2\) ならば \(a+b=3\)
\(p\):\(a=1\) かつ \(b=2\)
\(q\):\(a+b=3\)
\(p~\Rightarrow~q\) を考えると、
\(a=1\) かつ \(b=2\) のとき、$$~~~a+b=1+2=3$$よって、\(q\) を満たします。
よって、答えは真となります。
問題解説(3)
\({\small (3)}~x^2≧9\) ならば \(x≧3\)
\(p\):\(x^2≧9\)
\(q\):\(x≧3\)
\(p~\Rightarrow~q\) を考えると、
\(x=-4\) のとき、$$~~~x^2=(-4)^2=16≧9$$よって、\(p\) を満たすが、$$~~~x=-4≦3$$となるので、\(q\) を満たさない。
よって、答えは偽となります。また、反例の1つは、\(x=-4\) のときとなります。
問題解説(4)
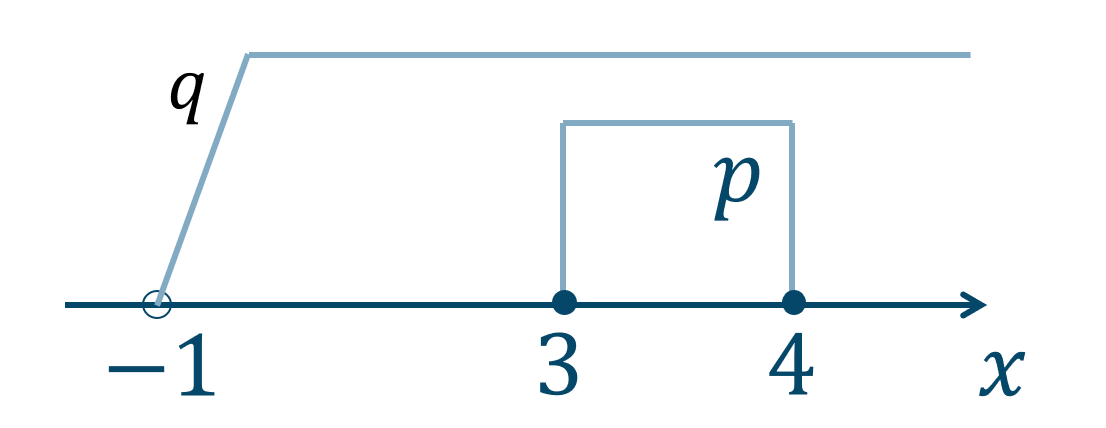
\({\small (4)}~3≦x≦4\) ならば \(-1<x\)
\(p\):\(3≦x≦4\)
\(q\):\(-1<x\)
\(p~\Rightarrow~q\) を考えると、
\(p~,~q\) を数直線上に表すと、
数直線より、\(p\) を満たすどんな \(x\) でも \(q\) を満たします。
よって、答えは真となります。
問題解説(5)
\({\small (5)}~n\) が3の倍数ならば \(n\) は6の倍数である
\(p\):\(n\) が3の倍数
\(q\):\(n\) が6の倍数
\(p~\Rightarrow~q\) を考えると、
\(n=9\) のとき、3の倍数であるので \(p\) を満たします。
\(n=9\) は、6の倍数でないので \(q\) を満たさない。
よって、答えは偽となります。また、反例の1つは、\(n=9\) のときとなります。
今回のまとめ
条件の真偽ではその真偽の判定方法と偽のときの反例の見つけ方に注意して問題を解きましょう。