条件の否定②（すべて・ある・ともに）

2018.04.222024.02.18

条件の否定②（すべて・少なくとも）

Point：すべて・ある・ともに・少なくともの否定■ すべて・あるの否定

すべての実数 \(x\) について \({\rm A}\)
　　　⇅否定
ある実数 \(x\) について \({\rm \overline {\,A\,}}\)

※ 「すべての実数 \(x\) について◯◯」は、
　「任意の実数 \(x\) について◯◯」
　「実数 \(x\) は常に◯◯」
　「◯◯を満たす \(x\) が存在する」

※ 「あるの実数 \(x\) について◯◯」は、
　「適当な実数 \(x\) について◯◯」
　「◯◯を満たす \(x\) が少なくとも１つ存在する」

■ ともに・少なくともの否定
２つの実数 \(x~,~y\) について、

\(x~,~y\) がともに \({\rm A}\)
　　　⇅否定
\(x~,~y\) の少なくとも一方が \({\rm \overline {\,A\,}}\)

※ ド・モルガンの法則を用いる。

©︎ 2024 教科書より詳しい高校数学 yorikuwa.com

問題次の条件の否定を答えよ。ただし、文字はすべて実数である。
\({\small (1)}~\)すべての実数 \(x\) について、\(x^2-4x+3>0\)

\(x^2-4x+3>0\) の否定は、\(x^2-4x+3≦0\) となります。
よって、答えは
「ある実数 \(x\) について、\(x^2-4x+3≦0\)」
となります。

問題次の条件の否定を答えよ。ただし、文字はすべて実数である。
\({\small (2)}~x^2+2x+3≦0\) を満たす実数 \(x\) が存在する

\(x^2+2x+3≦0\) の否定は、\(x^2+2x+3>0\) となります。
よって、答えは
「すべての実数 \(x\) について、\(x^2+2x+3>0\)」
となります。

問題次の条件の否定を答えよ。ただし、文字はすべて実数である。
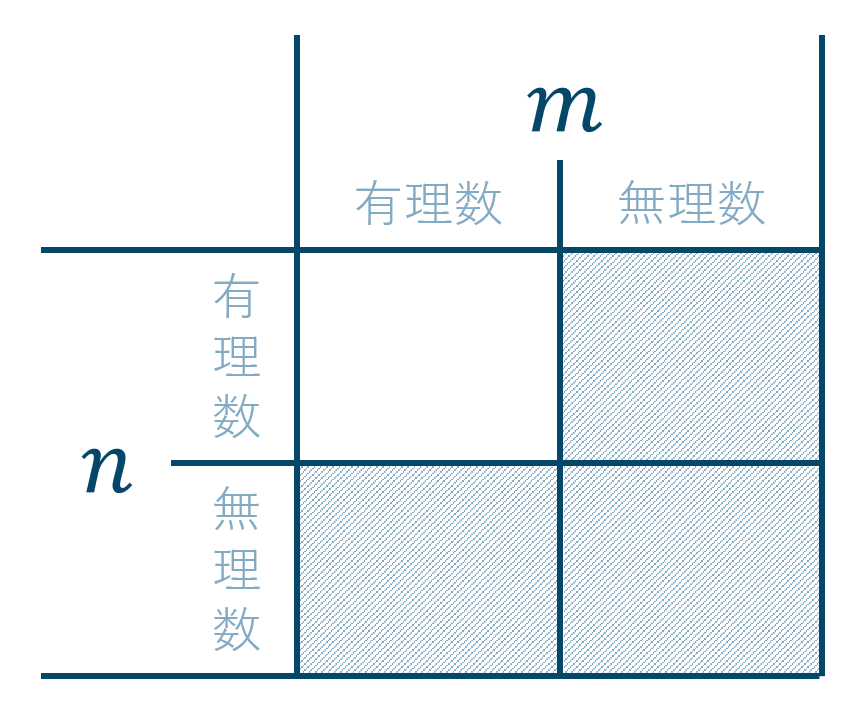
\({\small (3)}~m~,~n\) がともに有理数である

「\(m~,~n\) がともに有理数」の否定は、

この表より、答えは
「\(m~,~n\) の少なくとも一方が無理数」
となります。

「すべて〜」と「ある〜」は否定の関係となるので覚えておきましょう。また、「ともに〜」の表を用いて「少なくとも一方が〜」とできるようになりましょう。