必要条件と十分条件の判別
① 命題を矢印を用いて、\(p\,⇄\,q\) で表す。
② 行きと帰りのそれぞれの真偽を調べる。
\(p→q\) ( \(p\) ならば \(q\) )
\(p←q\) ( \(q\) ならば \(p\) )
③ 行き(十分条件)と帰り(必要条件)より、答え方を判別する。※ 真を○、偽を×とする。
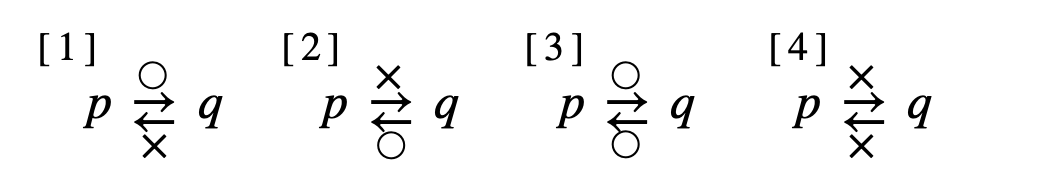
上の図より、\(p\) は \(q\) であるための、
\({\small [\,1\,]}~\)十分条件である。(必要条件ではない)
\({\small [\,2\,]}~\)必要条件である。(十分条件ではない)
\({\small [\,3\,]}~\)必要十分条件である。
※ このとき、互いに「同値」という。
\({\small [\,4\,]}~\)必要条件でも十分条件でもない。
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
問題解説:必要条件と十分条件
問題解説(1)
\({\small (1)}~p\):\(x^2=4\)、\(q\):\(x=2\)
\(p\):\(x^2=4~\Leftrightarrow~x=\pm2\)
\(q\):\(x=2\)
\(p~\Rightarrow~q\) は \(x=-2\) のとき、\(p\) は満たすが \(q\)を満たさないので偽となります。
\(q~\Rightarrow~p\) は常に成り立つので真となります。
よって、
となるので、答えは必要条件となります。
問題解説(2)
\({\small (2)}~p\):\(x~,~y\) がともに有理数、\(q\):\(xy\)が有理数
\(p\):\(x~,~y\) がともに有理数
\(q\):\(xy\) が有理数
\(p~\Rightarrow~q\) は常に成り立つので真となります。
\(q~\Rightarrow~p\) は \(x=\sqrt{2}~,~y=\sqrt{2}\) のとき、\(q\) は満たすが \(p\) は満たさないので偽となります。
よって、
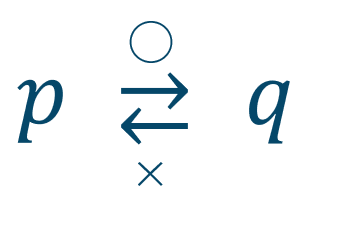
となるので、答えは十分条件となります。
問題解説(3)
\({\small (3)}~p\):\(xy>0\)、\(q\):\(x>0\) かつ \(y>0\)
\(p\):\(xy>0\)
\(q\):\(x>0\) かつ \(y>0\)
\(p~\Rightarrow~q\) は \(x=-1~,~y=-2\) のとき、\(p\) は満たすが \(q\)を満たさないので偽となります。
\(q~\Rightarrow~p\) は常に成り立つので真となります。
よって、
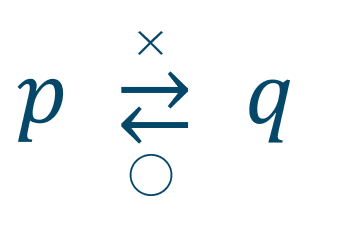
となるので、答えは必要条件となります。
問題解説(4)
\({\small (4)}~p\):ある四角形がひし形、\(q\) :ある四角形が平行四辺形
\(p\):四角形がひし形
\(q\):四角形が平行四辺形
平行四辺形の分類図は次のようになります。
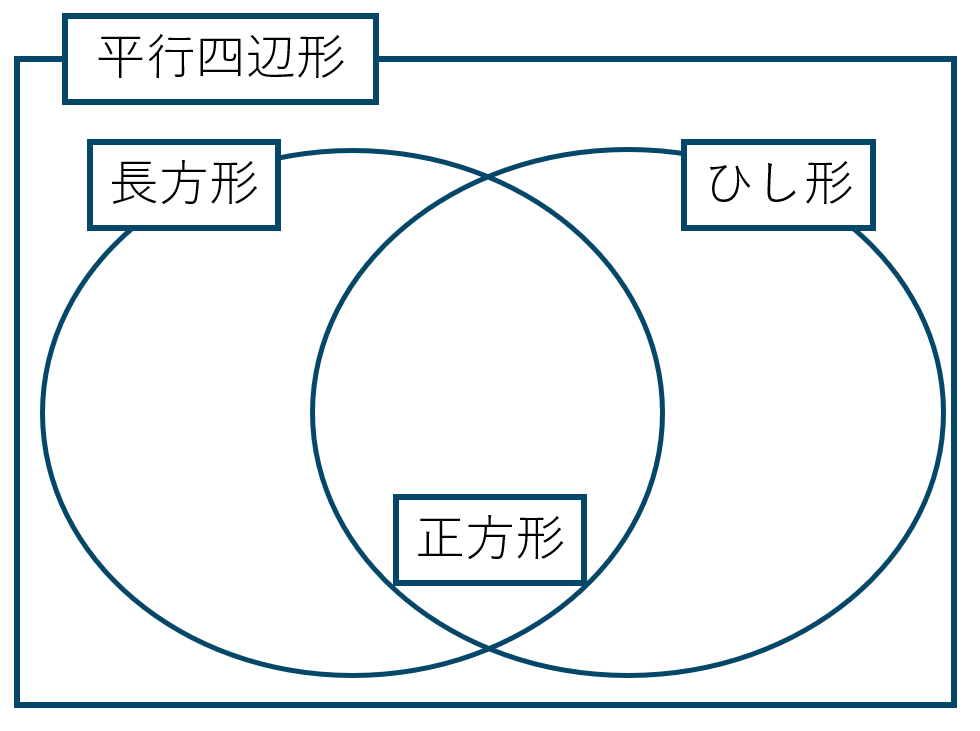
これより、\(p~\Rightarrow~q\) は常に成りたち真となり
\(q~\Rightarrow~p\) は反例があり偽となります。
よって、
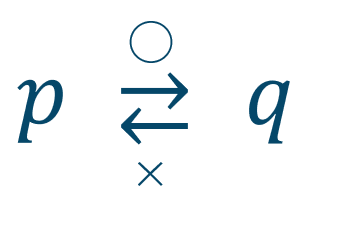
となるので、答えは十分条件となります。
問題解説(5)
\({\small (5)}~p\):2つの正方形が合同、\(q\):2つの正方形の面積が等しい
\(p\):2つの正方形が合同
\(q\):2つの正方形の面積が等しい
\(p~\Rightarrow~q\) は合同であれば、面積が等しくなるので真となります。
\(q~\Rightarrow~p\) は正方形であるので面積が等しいとき、1辺の長さも等しくなるので2つの正方形は合同になります。よって、真となります。
これらより、

となるので、答えは必要十分条件となります。
今回のまとめ
必要条件と十分条件の解法の手順と判定方法はできるように練習しておきましょう。また、様々な数学的知識も必要となりますので覚えておきましょう。




