逆・裏・対偶の解法
Point:逆・裏・対偶とその性質命題 \(p~\Rightarrow~q\) ( \(p\) ならば \(q\) ) に対して、
逆は、 \(q~\Rightarrow~p\) ( \(q\) ならば \(p\) )
裏は、 \(\overline {\,p\,}~\Rightarrow~\overline {\,q\,}\) ( \(\overline {\,p\,}\) ならば \(\overline {\,q\,}\) )
対偶は、\(\overline {\,q\,}~\Rightarrow~\overline {\,p\,}\) ( \(\overline {\,q\,}\) ならば \(\overline {\,p\,}\) )

命題の真偽とその対偶の真偽は一致するので、
命題 \(p~\Rightarrow~q\) と 対偶 \(\overline {\,q\,}~\Rightarrow~\overline {\,p\,}\)
命題 \(q~\Rightarrow~p\) と 対偶 \(\overline {\,p\,}~\Rightarrow~\overline {\,q\,}\)
の真偽はそれぞれ一致する。
逆は、 \(q~\Rightarrow~p\) ( \(q\) ならば \(p\) )
裏は、 \(\overline {\,p\,}~\Rightarrow~\overline {\,q\,}\) ( \(\overline {\,p\,}\) ならば \(\overline {\,q\,}\) )
対偶は、\(\overline {\,q\,}~\Rightarrow~\overline {\,p\,}\) ( \(\overline {\,q\,}\) ならば \(\overline {\,p\,}\) )
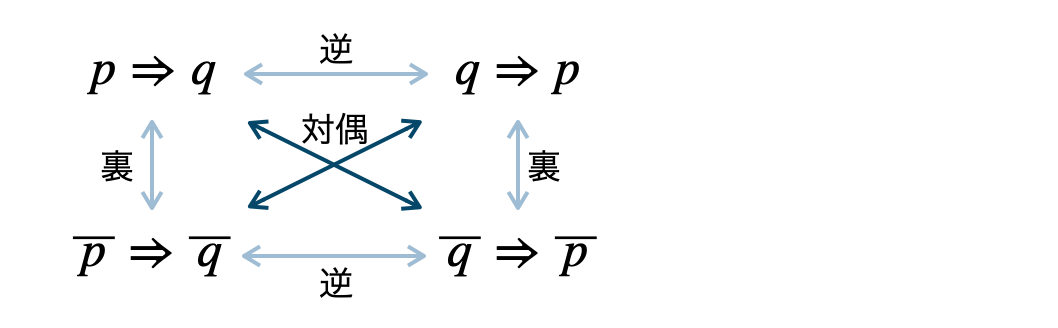
※ \(q~\Rightarrow~p\) と \(\overline {\,p\,}~\Rightarrow~\overline {\,q\,}\) も対偶の関係
命題の真偽とその対偶の真偽は一致するので、
命題 \(p~\Rightarrow~q\) と 対偶 \(\overline {\,q\,}~\Rightarrow~\overline {\,p\,}\)
命題 \(q~\Rightarrow~p\) と 対偶 \(\overline {\,p\,}~\Rightarrow~\overline {\,q\,}\)
の真偽はそれぞれ一致する。
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
問題解説:逆・裏・対偶
問題次の命題の逆と裏と対偶を答えよ。また、それぞれの真偽も答えよ。
\(x=2\) かつ \(y=3\) ならば \(xy=6\)
\(x=2\) かつ \(y=3\) ならば \(xy=6\)
命題「\(x=2\) かつ \(y=3\) ならば \(xy=6\)」についてこの命題は真となります。
この命題の逆は、
「\(xy=6\) ならば \(x=2\) かつ \(y=3\)」となります。
これは、\(x=1\) かつ \(y=6\) のとき満たさないので偽となります。
この命題の裏は、
「\(x\neq2\) または \(y\neq3\) ならば \(xy\neq6\)」となります。
この真偽は、対偶の関係に逆が偽であるので、これも偽となります。
この命題の対偶は、
「\(xy\neq6\) ならば \(x\neq2\) または \(y\neq3\)」となります。
この真偽は、対偶の関係にあるもとの命題が真であるので、これも真となります。
今回のまとめ
逆と裏と対偶についてはその表し方と対偶の関係にあるとき真偽が一致する性質をしっかりと覚えておきましょう。

【問題一覧】数学Ⅰ:集合と論理
このページは「高校数学Ⅰ:集合と論理」の問題一覧ページとなります。解説の見たい単元名がわからないとき...


