２次方程式の解の求め方
( ⅰ ) 左辺が因数分解できる場合$$~~~(x-\alpha)(x-\beta)=0$$と因数分解できると、解は$$~~~x=\alpha~,~\beta$$となります。
( ⅱ ) 因数分解できない場合
解の公式を用いると、
となります。
問題解説：２次方程式の解
問題解説(1)
$$~~~x^2-4x-5=0$$左辺を因数分解すると、$$~~~(x+1)(x-5)=0$$$$\hspace{ 65 pt}x=-1~,~5$$よって、答えは$$~~~x=-1~,~5$$となります。
問題解説(2)
$$~~~2x^2+5x-3=0$$左辺をす因数分解ると、たすき掛けの表より、
$$~~(2x-1)(x+3)=0$$\(2x-1=0\) より、$$\hspace{ 10 pt}2x-1=0$$移項して、両辺を \(2\) で割ると、$$\hspace{ 10 pt}2x=1$$$$\hspace{ 15 pt}x=\frac{1}{2}$$また、\(x+3=0\) より、$$\hspace{ 10 pt}x+3=0$$$$\hspace{ 27 pt}x=-3$$よって、答えは$$~~~x=\frac{1}{2}~,~-3$$となります。
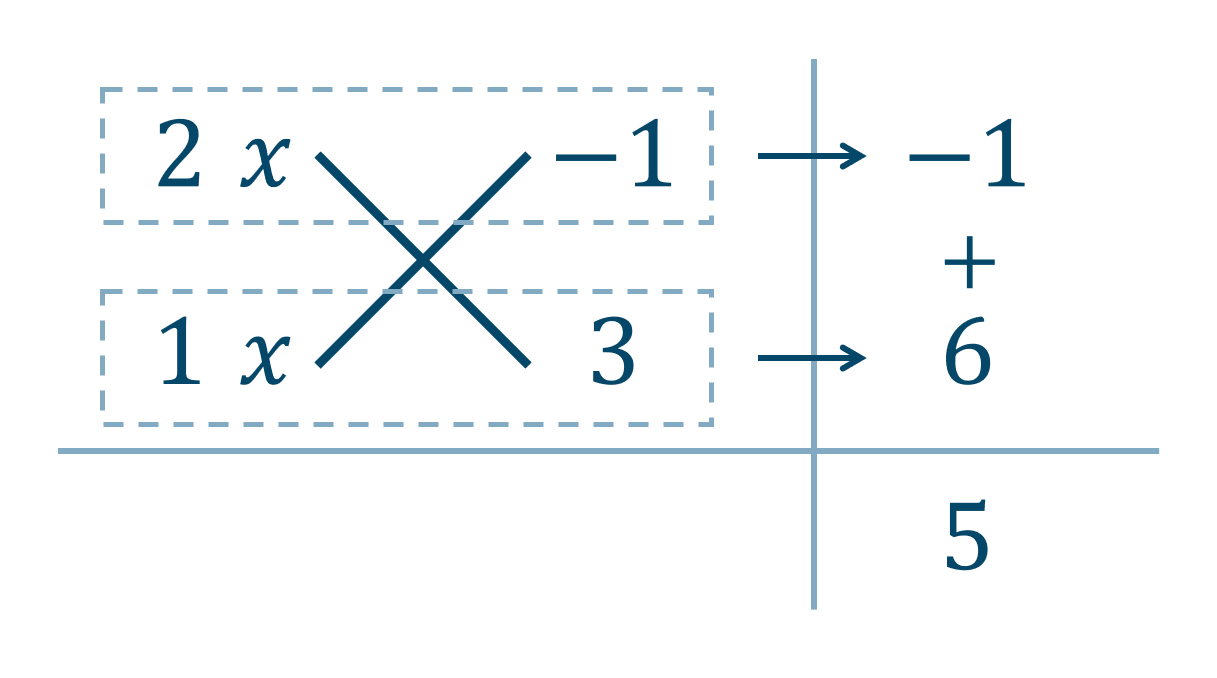
問題解説(3)
左辺が因数分解できないので、解の公式を用いると、$$\hspace{ 10 pt}x=\frac{-(-5)\pm\sqrt{(-5)^2-4\cdot2\cdot1}}{2\cdot2}$$$$\hspace{ 18 pt}=\frac{5\pm\sqrt{25-8}}{4}$$$$\hspace{ 18 pt}=\frac{5\pm\sqrt{17}}{4}$$よって、答えは$$~~~x=\frac{5\pm\sqrt{17}}{4}$$となります。
問題解説(4)
左辺が因数分解できないので、解の公式を用いると、$$\hspace{ 10 pt}x=\frac{-(-5)\pm\sqrt{(-4)^2-4\cdot1\cdot1}}{2\cdot1}$$$$\hspace{ 18 pt}=\frac{4\pm\sqrt{16-4}}{2}$$$$\hspace{ 18 pt}=\frac{4\pm\sqrt{12}}{2}$$$$\hspace{ 18 pt}=\frac{4\pm2\sqrt{3}}{2}$$分子の各項をそれぞれ \(2\) で割ると、$$\hspace{ 18 pt}=2\pm\sqrt{3}$$よって、答えは$$~~~x=2\pm\sqrt{3}$$となります。
今回のまとめ
２次方程式の解の求め方は、因数分解できるかできないかで解法が変わってきます。解の公式も使えるように練習しておきましょう。
