解が与えられた２次方程式

2018.08.152020.06.09

解が与えられた２次方程式の解法
問題解説：解が与えられた２次方程式
今回のまとめ

解が与えられた２次方程式の解法

Point：解が与えられた２次方程式２次方程式の１つの解が与えられたときは、
① その解 $x=\alpha$ を２次方程式に代入した式を条件式とします。
② 条件式を解き、未知数となっている係数の値を求めます。
③ 求めた係数の値を２次方程式に当てはめて、できた２次方程式から他の解を求めます。

問題解説：解が与えられた２次方程式

問題次の２次方程式の解の１つが $x=2$ であるとき、$k$ の値ともう１つの解を求めよ。$$~~~2x^2+(k+2)x+2k=0$$

$$\hspace{ 10 pt}2x^2+(k+2)x+2k=0~~~\cdots{\large ①}$$解が $x=2$ であることより、①に代入しても成り立つので、$$\hspace{ 10 pt}2\cdot2^2+(k+2)\cdot2+2k=0$$$$\hspace{ 43 pt}8+2k+4+2k=0$$$$\hspace{ 78 pt}4k+12=0$$移項して両辺を $4$ で割ると、$$\hspace{ 10 pt}4k=-12$$$$\hspace{ 15 pt}k=-3$$
次に、これを①に代入すると、$$\hspace{ 10 pt}2x^2+(-3+2)x+2\cdot(-3)=0$$$$\hspace{ 76 pt}2x^2-x-6=0$$左辺を因数分解すると、たすき掛けの表より、
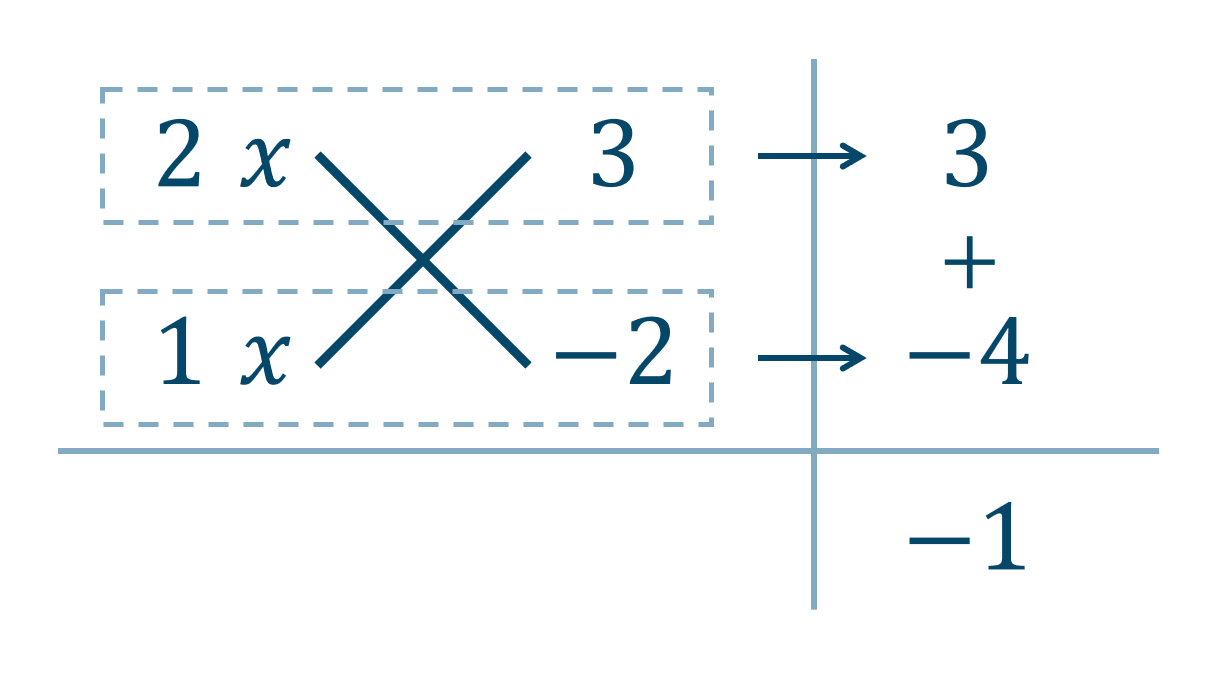
$$\hspace{ 10 pt}(2x+3)(x-2)=0$$よって、$2x+3=0$ より、$$\hspace{ 10 pt}2x+3=0$$移項して、両辺を $2$ で割ると、$$\hspace{ 10 pt}2x=-3$$$$\hspace{ 15 pt}x=-\frac{3}{2}$$
したがって、答えは$$~~~k=-3~,~x=-\frac{3}{2}$$となります。