２次関数とx軸との交点の解法
よって、２次方程式の解の判別式を \(D\) とすると、
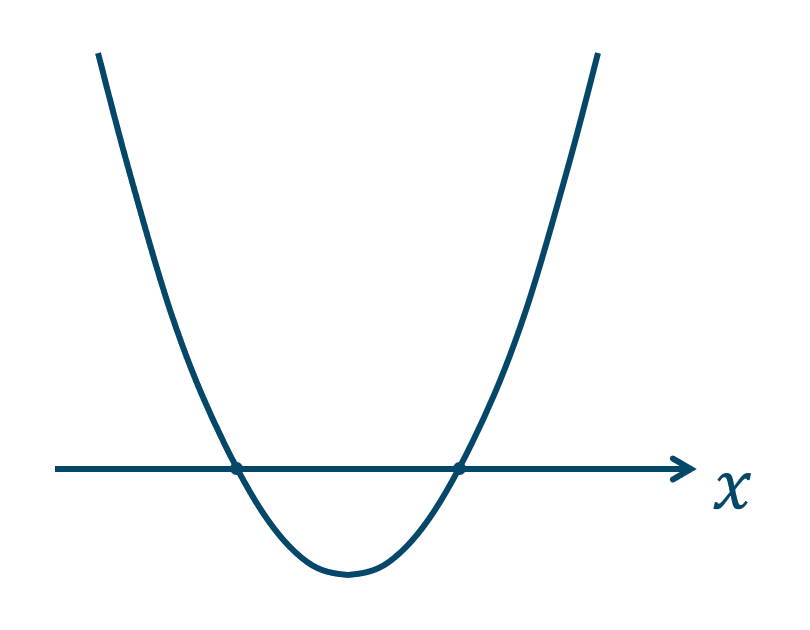
( ⅰ ) \(D>0\) のとき
２次方程式の解が２個となるので、この２次関数は \(x\) 軸と２点で交わります。
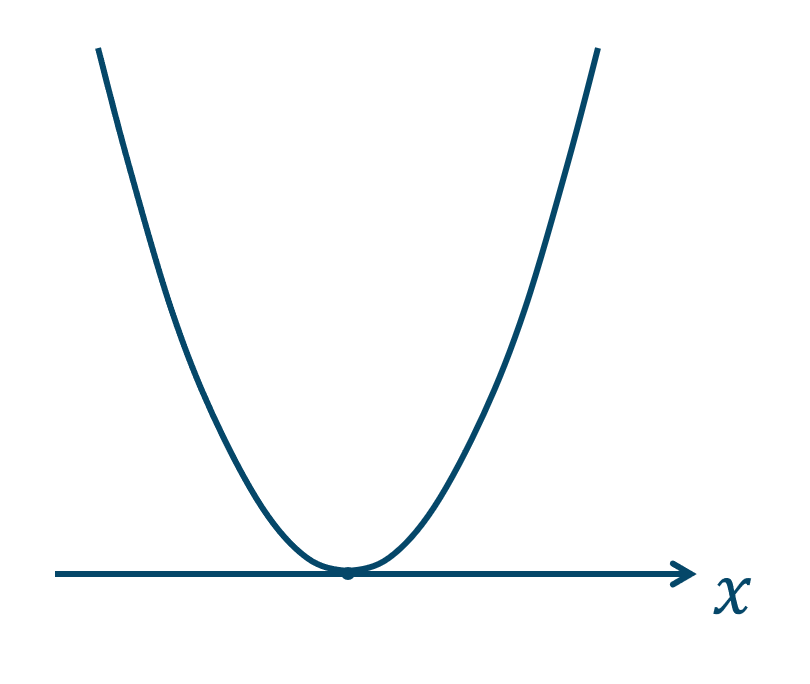
( ⅱ ) \(D=0\) のとき
２次方程式の解が１個(重解)となるので、この２次関数は \(x\) 軸と接します。(交点が１個)
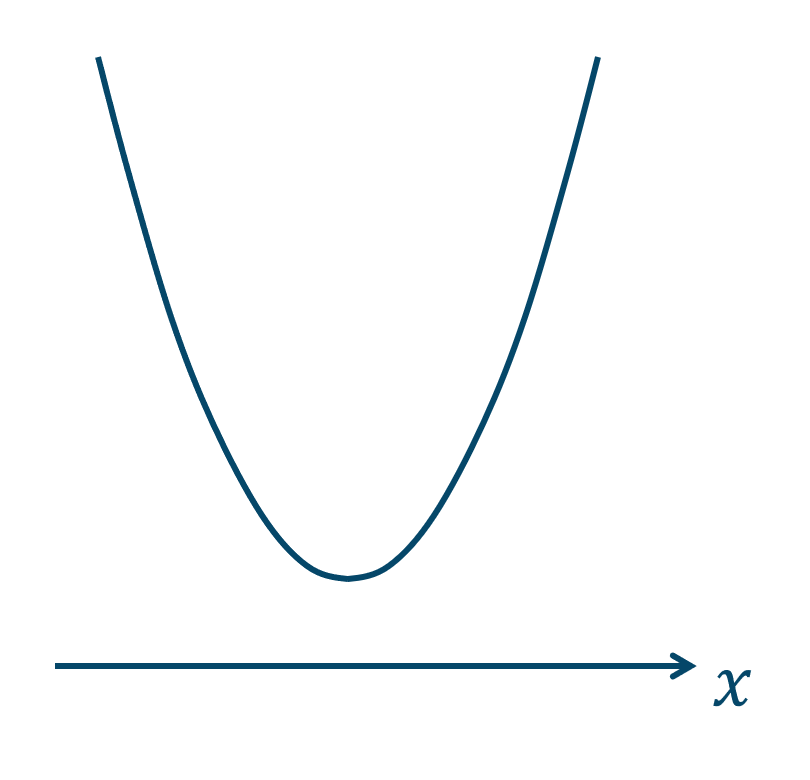
( ⅲ ) \(D<0\) のとき
２次方程式の解なしとなるので、この２次関数は \(x\) 軸と交点なしとなります。
問題解説：２次関数とx軸との交点
問題解説(1)
\(3x^2-7x+2=0\) とすると、この２次方程式の判別式 \(D\) は、$$\hspace{ 10 pt}D=(-7)^2-4\cdot3\cdot2$$$$\hspace{ 20 pt}=49-24$$$$\hspace{ 20 pt}=25>0$$よって、\(D>0\) となるので、この２次関数は \(x\) 軸と異なる２点で交わります。
また、その交点の座標は、次の２次方程式を解くことで \(x\) 座標が求まります。$$\hspace{ 10 pt}3x^2-7x+2=0$$左辺を因数分解すると、たすき掛けの表より、
$$\hspace{ 10 pt}(3x-1)(x-2)=0$$よって、\(3x-1=0\) より、$$\hspace{ 10 pt}3x-1=0$$移項して、 \(3\) で割ると、$$\hspace{ 10 pt}3x=1$$$$\hspace{ 15 pt}x=\frac{1}{3}$$また、\(x-2=0\) より、$$\hspace{ 10 pt}x-2=0$$移項すると、$$\hspace{ 20 pt}x=2$$よって、交点の座標は$$~~~\left(\frac{1}{3}~,~0\right)~,~(2~,~0)$$となります。
問題解説(2)
\(-x^2-2x-3=0\) とすると、この２次方程式の判別式 \(D\) は、$$\hspace{ 10 pt}D=(-2)^2-4\cdot(-1)\cdot(-3)$$$$\hspace{ 20 pt}=4-12$$$$\hspace{ 20 pt}=-8<0$$よって、\(D<0\) となるので、この２次関数は \(x\) 軸と交わらないとなります。
問題解説(3)
\(x^2-6x+9=0\) とすると、この２次方程式の判別式 \(D\) は、$$\hspace{ 10 pt}D=(-6)^2-4\cdot1\cdot9$$$$\hspace{ 20 pt}=36-36$$$$\hspace{ 20 pt}=0$$よって、\(D=0\) となるのでこの２次関数は \(x\) 軸と異なる１点で交わります。（\(x\) 軸と接する。）
また、その交点の座標は、次の２次方程式を解くことで \(x\) 座標が求まります。$$\hspace{ 10 pt}x^2-6x+9=0$$左辺を因数分解すると、$$\hspace{ 10 pt}(x-3)^2=0$$よって、\(x-3=0\) より、$$\hspace{ 10 pt}x-3=0$$移項すると、$$\hspace{ 20 pt}x=3$$よって、交点の座標は$$~~~(3~,~0)$$となります。
今回のまとめ
２次関数と \(x\) 軸との交点の座標についての問題は、与えられた２次関数の右辺より２次方程式を作りその２次方程式の解についての問題にしましょう。
