三角比と不等式

2018.08.232020.06.09

三角比と不等式を満たす角
問題解説：三角比と不等式
今回のまとめ

三角比と不等式を満たす角

Point：三角比と不等式不等式を単位円上に表して求めます。
( ⅰ ) $\cos{\theta}≦a$ のとき
$x$ 座標の値が $a$ 以下となるので、単位円上で直線 $x=a$ より左側の範囲となります。

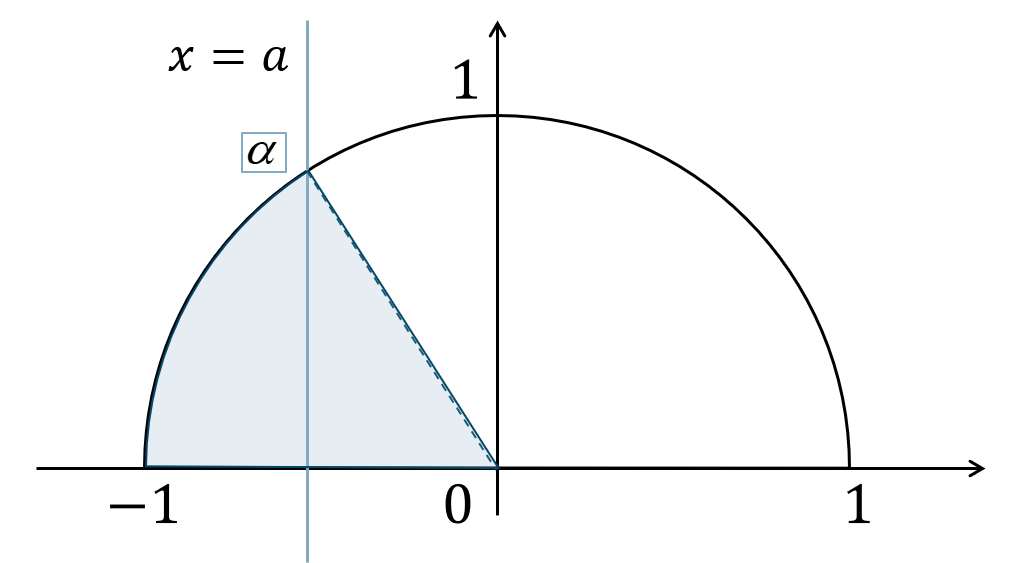
よって、図より解は$$~~~\alpha≦\theta≦180^\circ$$となります。

( ⅱ ) $\sin{\theta}>b$ のとき
$y$ 座標の値が $b$ より大きいとなるので、単位円上で直線 $y=b$ より上側の範囲となります。

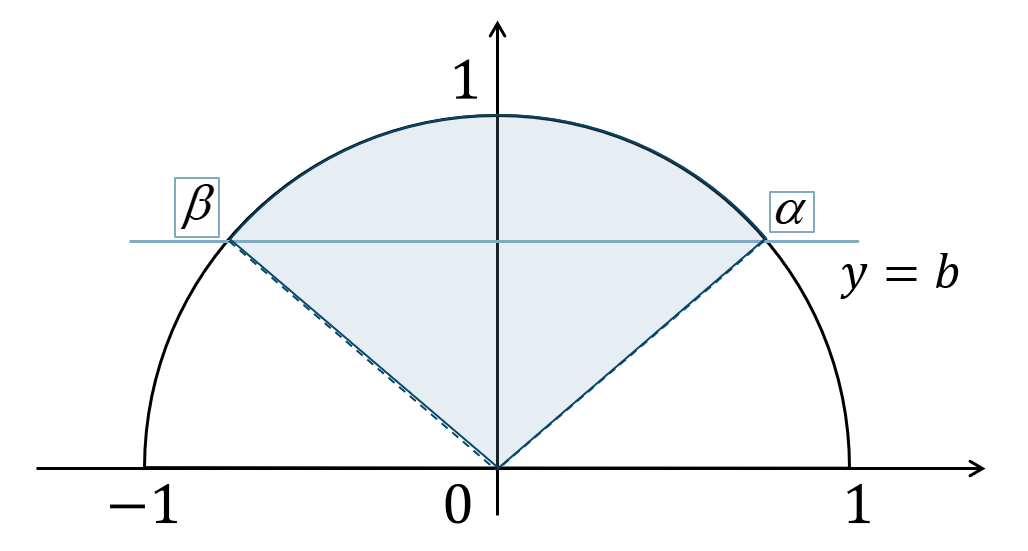
よって、図より解は$$~~~\alpha<\theta<\beta$$となります。

( ⅲ ) $\tan{\theta}≧m$ のとき
傾きが $m$ 以上となるので、単位円上で直線 $y=mx$ を引いて考えると、

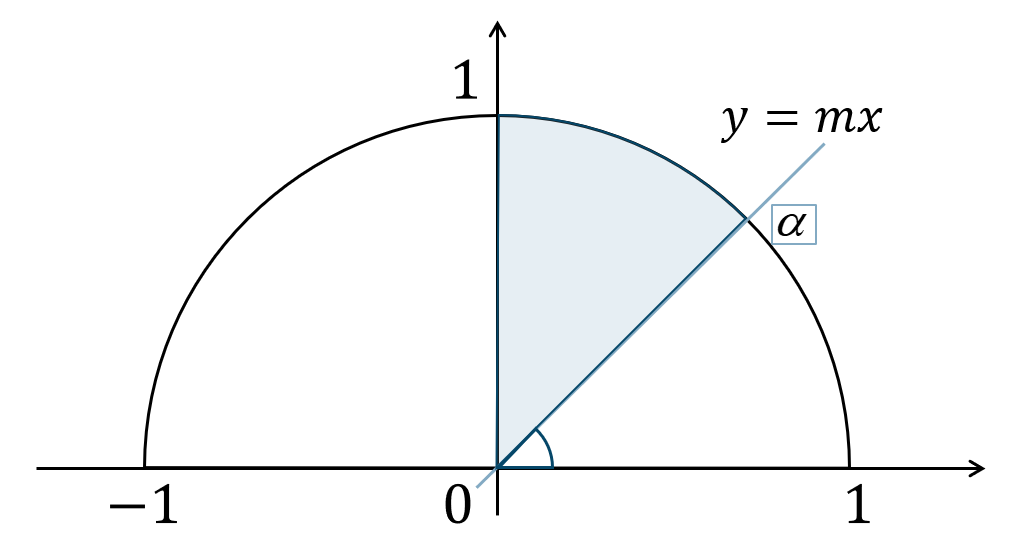
よって、図より解は$$~~~\alpha≦\theta<90^\circ$$となります。
このとき、$\tan{90^\circ}$ は解なしとなるので含みません。

このとき、以下の表を使いましょう。
$30^\circ \times n$ の角の場合

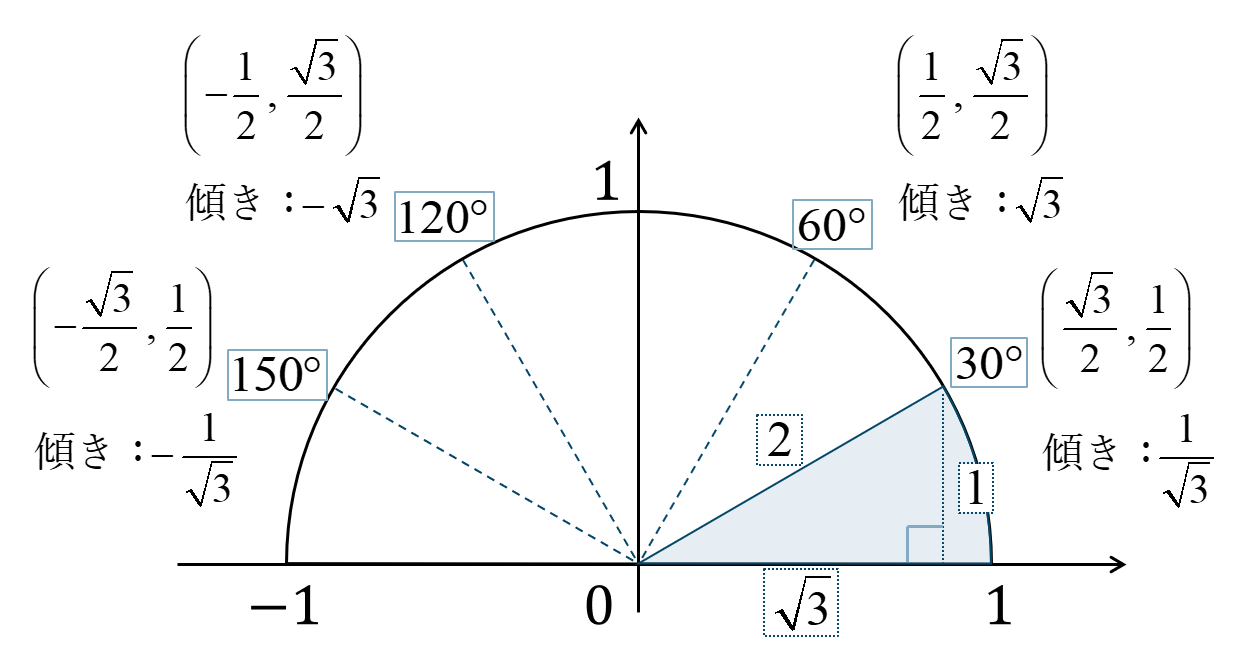
$45^\circ \times n$ の角の場合

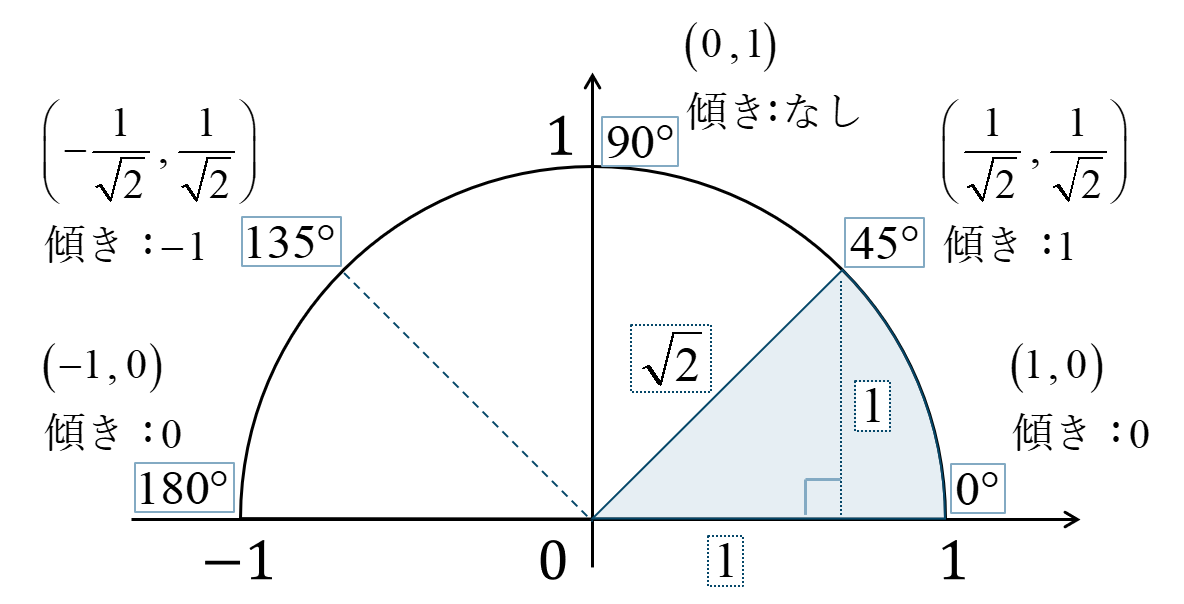
問題解説：三角比と不等式

問題解説(1)

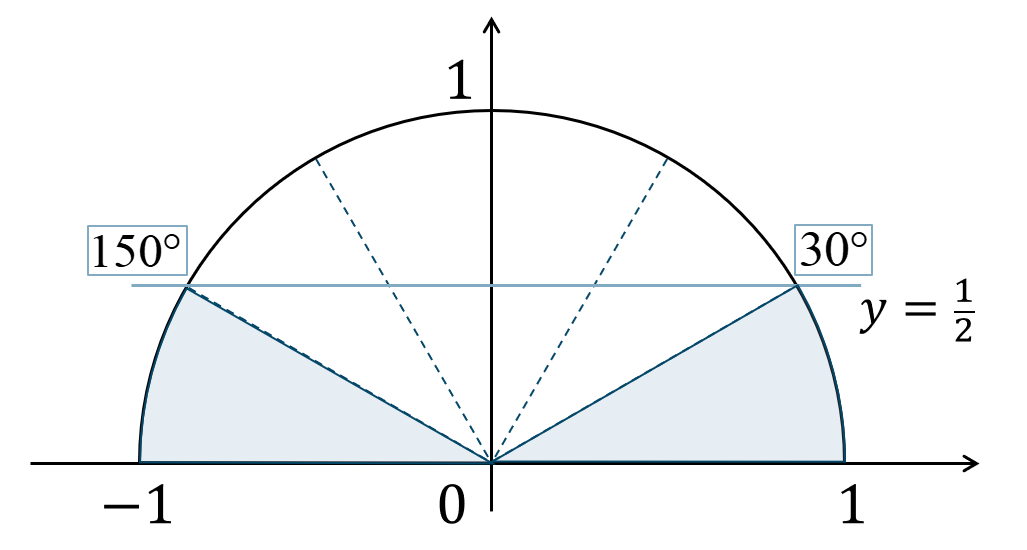
問題次の不等式を満たす $\theta$ の範囲を求めよ。ただし、$0^\circ≦\theta≦180^\circ$ とする。$${\small (1)}~\sin{\theta}≦\frac{1}{2}$$

単位円上に表すと、$y$ 座標が ${\Large \frac{1}{2}}$ 以下となればよいので、

よって、$0^\circ≦\theta≦180^\circ$ の範囲で考えると答えは、$$~~~0^\circ≦\theta≦30^\circ~,~150^\circ≦\theta≦180^\circ$$となります。

問題解説(2)

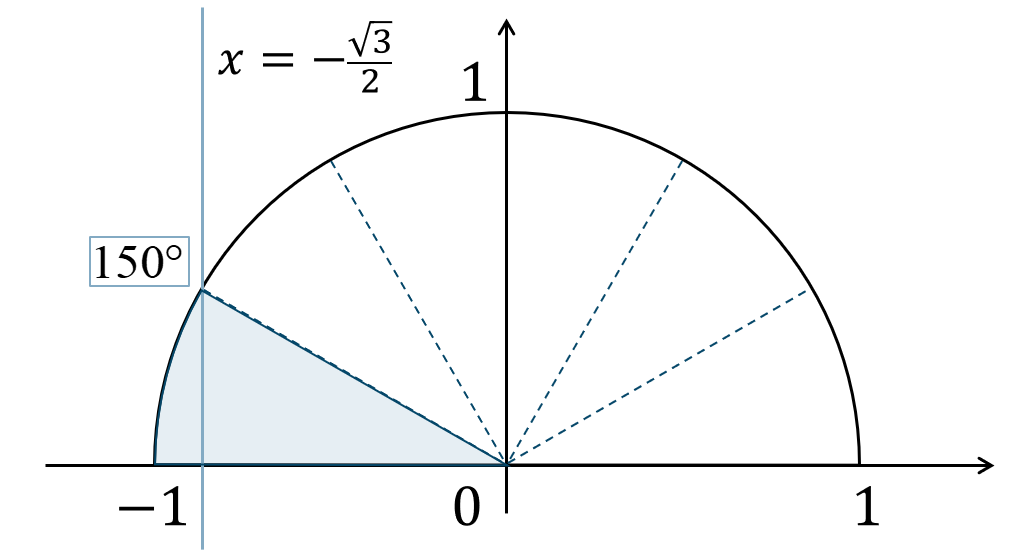
問題次の不等式を満たす $\theta$ の範囲を求めよ。ただし、$0^\circ≦\theta≦180^\circ$ とする。$${\small (2)}~\cos{\theta}<-\frac{\sqrt{3}}{2}$$

単位円上に表すと、$x$ 座標が $-{\Large \frac{\sqrt{3}}{2}}$ より小さくなればよいので、

よって、$0^\circ≦\theta≦180^\circ$ の範囲で考えると答えは、$$~~~150^\circ<\theta≦180^\circ$$となります。

問題解説(3)

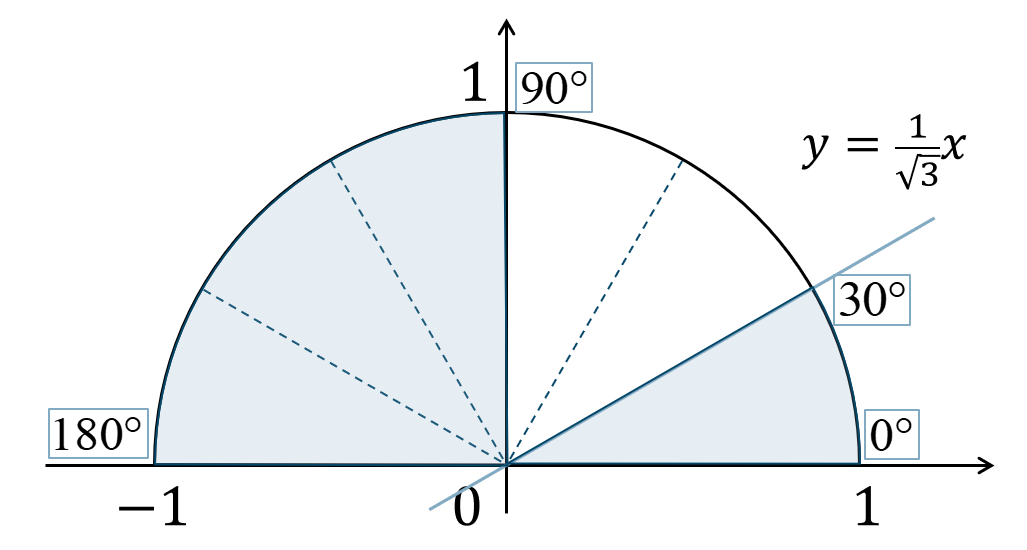
問題次の不等式を満たす $\theta$ の範囲を求めよ。ただし、$0^\circ≦\theta≦180^\circ$ とする。$${\small (3)}~\tan{\theta}≦\frac{1}{\sqrt{3}}$$

単位円上に表すと、傾きが ${\Large \frac{1}{\sqrt{3}}}$ 以下となればよいので、

よって、$0^\circ≦\theta≦180^\circ$ の範囲で考えると、$$~~~0^\circ≦\theta≦30^\circ$$となります。
また、第２象限 $90^\circ<\theta≦180$ の範囲は傾きが $m<0$ となるので成り立ちます。
したがって、答えは、$$~~~0^\circ≦\theta≦30^\circ~,~90^\circ<\theta≦180^\circ$$となります。