直線の傾きと正接の解法
Point:直線の傾きと正接\(\tan{\theta}\) の値は次の図の直線の傾きと同じになります。

よって、直線の式が \(y=mx\) のとき、
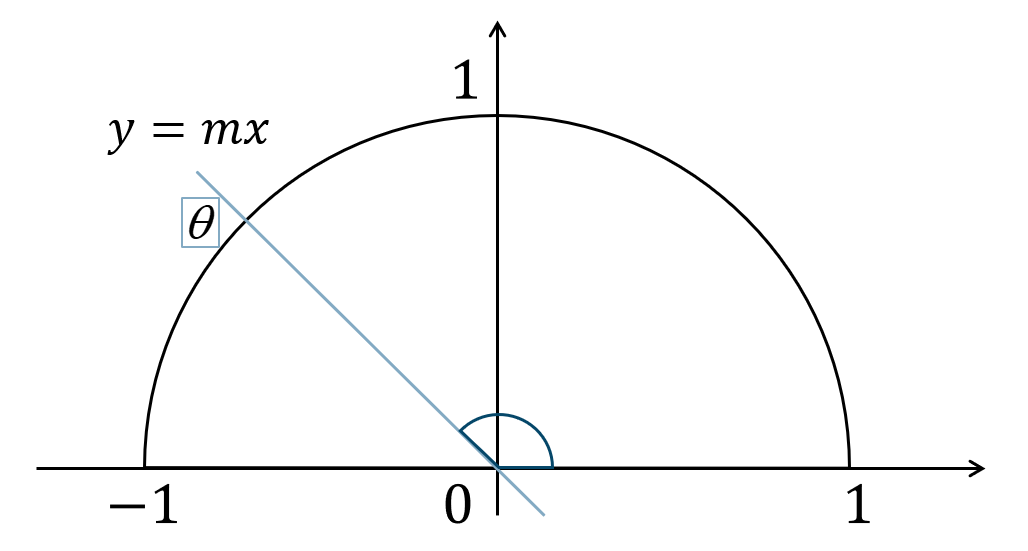
よって、直線の式が \(y=mx\) のとき、
$$\tan{\theta}=m$$
これより、\(x\) 軸の正の部分となす角を求めることができます。
問題解説:直線の傾きと正接
問題解説(1)
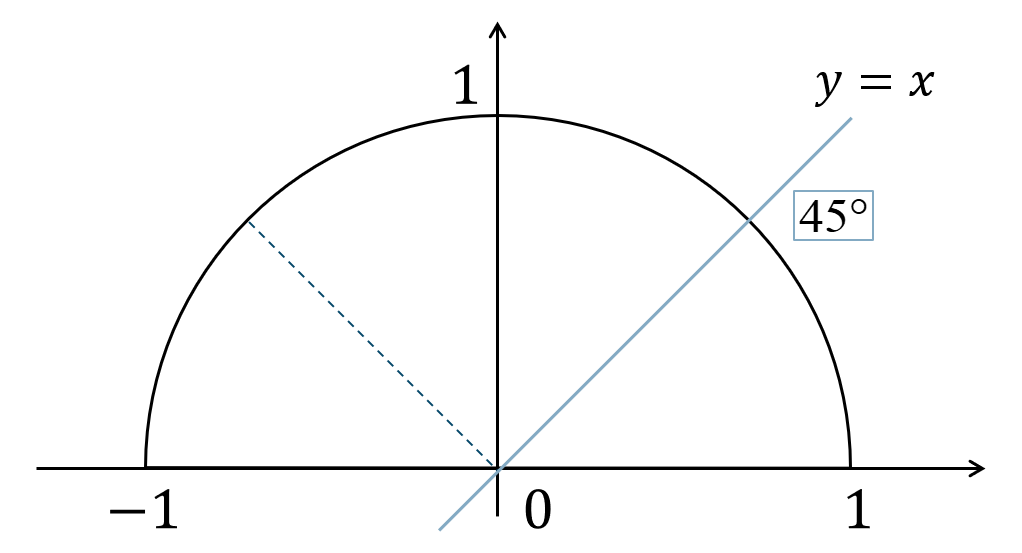
問題次の直線の式のグラフと \(x\) 軸の正の部分からなす角を \(\theta\) を求めよ。$${\small (1)}~y=x$$
\(\tan{\theta}=1\) となるので、単位円上に表すと、
これより、直線と円との交点より角を読み取ると、
答えは$$~~~45^\circ$$となります。
問題解説(2)
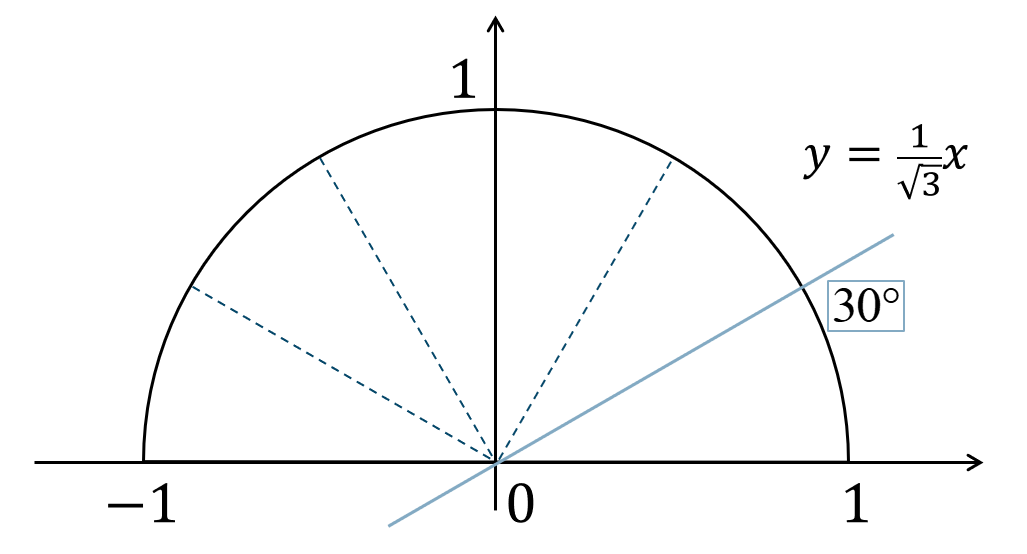
問題次の直線の式のグラフと \(x\) 軸の正の部分からなす角を \(\theta\) を求めよ。$${\small (2)}~y=\frac{1}{\sqrt{3}}x$$
\(\tan{\theta}={\Large \frac{1}{\sqrt{3}}}\) となるので、単位円上に表すと、
これより、直線と円との交点より角を読み取ると、
答えは$$~~~30^\circ$$となります。
問題解説(3)
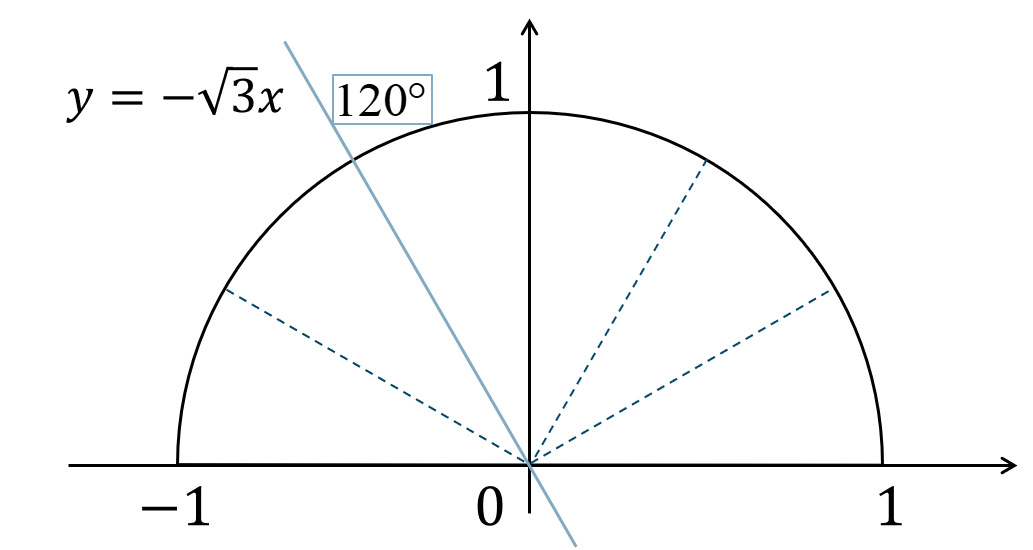
問題次の直線の式のグラフと \(x\) 軸の正の部分からなす角を \(\theta\) を求めよ。$${\small (3)}~y=-\sqrt{3}x$$
\(\tan{\theta}=-\sqrt{3}\) となるので、単位円上に表すと、
これより、直線と円との交点より角を読み取ると、
答えは$$~~~120^\circ$$となります。
今回のまとめ
直線のグラフと \(x\) 軸とのなす角は、\(\tan{\theta}\) の値と単位円を用いて求めましょう。

【問題一覧】数学Ⅰ:図形と計量
このページは「高校数学Ⅰ:図形と計量」の問題一覧ページとなります。解説の見たい単元名がわからないとき...