度数分布表

度数分布表とヒストグラム
問題：度数分布表
今回のまとめ

度数分布表とヒストグラム

Point：度数分布表とヒストグラムデータを適当な区間に分けて、その区間ごとにデータの個数を集計したものを度数分布表といいます。
・それぞれの区間を「階級」
・区間の幅を「階級の幅」
・区間の中央値を「階級値」
・各階級ほ中のデータの個数を「度数」

以上〜未満	階級値	度数
$0$ 〜 $10$	$5$	$2$
$10$ 〜 $20$	$15$	$5$
$20$ 〜 $30$	$25$	$3$
合計		$10$

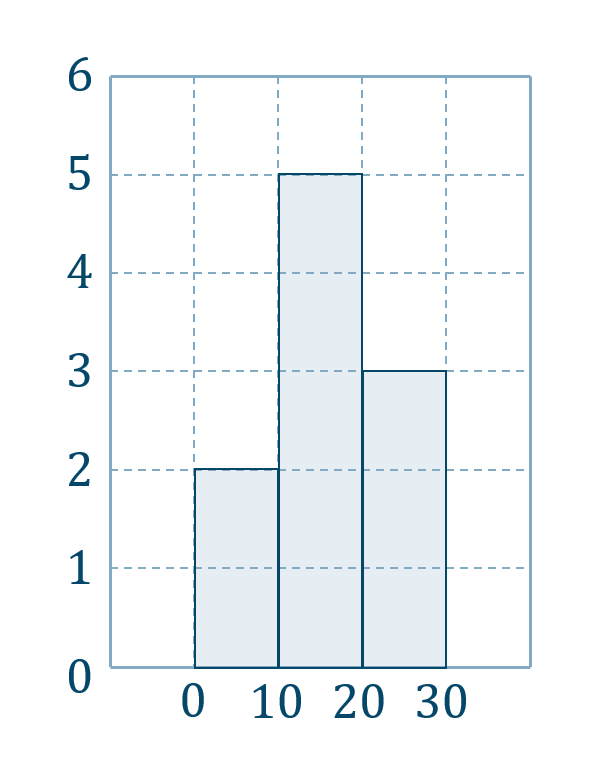
また、この度数分布表を柱状のグラフで表したものをヒストグラムといいます。

Point：相対度数

階級の度数を度数の合計で割ったものを相対度数といいます。

以上〜未満	度数	相対度数
$0$ 〜 $10$	$2$	$0.2$
$10$ 〜 $20$	$5$	$0.5$
$20$ 〜 $30$	$3$	$0.3$
合計	$10$	$1$

Point：度数分布表と代表値・度数分布表と平均値
（階級値）×（度数）の和を度数の合計で割ります。

以上〜未満	階級値	度数	階級値×度数
$0$ 〜 $10$	$5$	$2$	$5\times2$
$10$ 〜 $20$	$15$	$5$	$15\times5$
$20$ 〜 $30$	$25$	$3$	$25\times3$
合計		$10$

この度数分布表での平均値は

$$\frac{5\times2+15\times5+25\times3}{10}$$

となります。

・度数分布表と中央値
度数の合計より、中央の値のある階級の階級値が中央値となります。また、２つの階級にまたがっているときはその２つの階級値の平均が中央値となります。

・度数分布表と最頻値
度数が最も多い階級の階級値が最頻値となります。

問題：度数分布表

問題解説(1)

問題次のデータについて、以下の問いに答えよ。$$~~~10\hspace{ 10 pt}14\hspace{ 10 pt}~~4\hspace{ 10 pt}~~9\hspace{ 10 pt}~~9\hspace{ 10 pt}22\hspace{ 10 pt}15\hspace{ 10 pt}~~3$$$$~~~~~2\hspace{ 10 pt}~~1\hspace{ 10 pt}~~8\hspace{ 10 pt}12\hspace{ 10 pt}~~6\hspace{ 10 pt}~~3\hspace{ 10 pt}13\hspace{ 10 pt}18$$$$~~~12\hspace{ 10 pt}~~5\hspace{ 10 pt}~~1\hspace{ 10 pt}18\hspace{ 10 pt}17\hspace{ 10 pt}13\hspace{ 10 pt}~~7\hspace{ 10 pt}~~7$$$$~~~10\hspace{ 10 pt}16\hspace{ 10 pt}11\hspace{ 10 pt}~~9\hspace{ 10 pt}24\hspace{ 10 pt}14\hspace{ 10 pt}~~2\hspace{ 10 pt}12$$${\small (1)}$ 度数分布表を作成せよ。ただし、階級は $0$ から始め、階級の幅は $5$ とする。

階級が $0$ 以上〜 $5$ 未満となるのは、$$~4~,~3~,~2~,~1~,~3~,~1~,~2$$の合計 $7$ 個となります。

階級が $5$ 以上〜 $10$ 未満となるのは、$$~9~,~9~,~8~,~6~,~5~,~7~,~7~,~9$$の合計 $8$ 個となります。

階級が $10$ 以上〜 $15$ 未満となるのは、$$~10~,~14~,~12~,~13~,~12~,~13~,~10~,~11~,~14~,~12$$の合計 $10$ 個となります。

階級が $15$ 以上〜 $20$ 未満となるのは、$$~15~,~18~,~18~,~17~,~16$$の合計 $5$ 個となります。

階級が $20$ 以上〜 $25$ 未満となるのは、$$~22~,~24$$の合計 $2$ 個となります。

以上より、度数分布表を作ると次のようになります。

以上〜未満	度数
$0$ 〜 $5$	$7$
$5$ 〜 $10$	$8$
$10$ 〜 $15$	$10$
$15$ 〜 $20$	$5$
$20$ 〜 $25$	$2$
合計	$32$

問題解説(2)

問題${\small (2)}$ ヒストグラムを作成せよ。

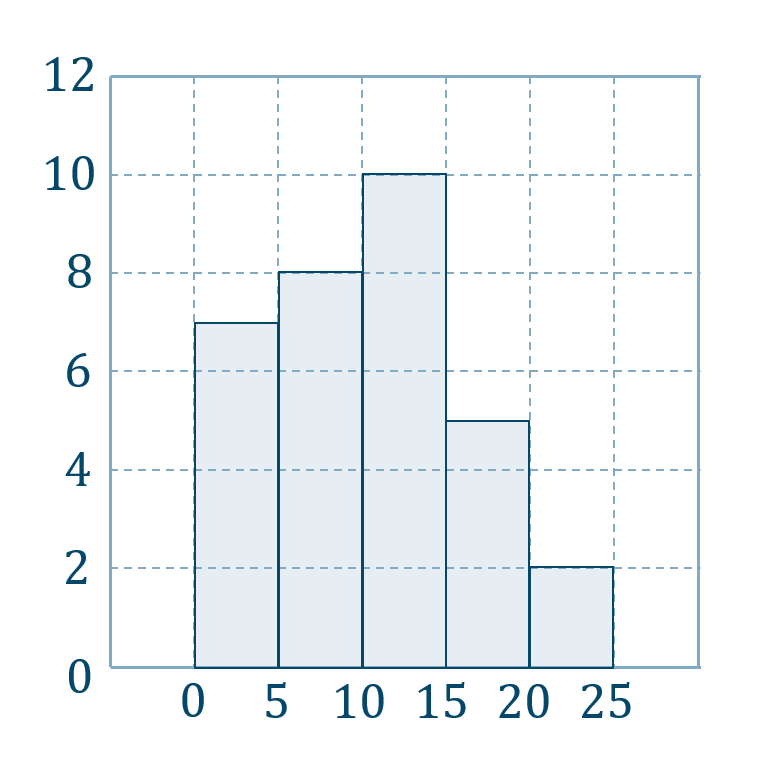
上の度数分布表より、ヒストグラムを作ると次のようになります。

問題解説(3)

問題${\small (3)}$ 階級値から平均値を求めよ。

度数分布表に階級値と（階級値）×（度数）を加えた表は次のようになります。

以上〜未満	階級値	度数	階級値×度数
$0$ 〜 $5$	$2.5$	$7$	$17.5$
$5$ 〜 $10$	$7.5$	$8$	$60$
$10$ 〜 $15$	$12.5$	$10$	$125$
$15$ 〜 $20$	$17.5$	$5$	$87.5$
$20$ 〜 $25$	$22.5$	$2$	$45$
合計		$32$

表より、（階級値）×（度数）の和は、$$~~~~~~17.5+60+125+87.5+45$$$$~=335$$また、データの個数は $32$ 個であるので平均値は、$$~~~\frac{335}{32}=10.46\cdots$$よって、答えは $10.5$ となります。

問題解説(4)

問題${\small (4)}$ 最頻値を求めよ。

度数分布表より、最も度数の多い階級値が最頻値となるので、答えは $12.5$ となります。

問題解説(5)

問題${\small (5)}$ 階級値より中央値を求めよ。

データの個数が $32$ より、その中央は$$~~~32\div2=16$$よって、$16$ 番目と $17$ 番目の平均となります。次に度数分布表より、その階級までの度数の和を表で表すと、

以上〜未満	階級値	度数	度数の累計
$0$ 〜 $5$	$2.5$	$7$	$7$
$5$ 〜 $10$	$7.5$	$8$	$15$
$10$ 〜 $15$	$12.5$	$10$	$25$
$15$ 〜 $20$	$17.5$	$5$	$32$
$20$ 〜 $25$	$22.5$	$2$	$32$
合計		$32$

よって、表より $16$ 番目と $17$ 番目は $10$ 以上 $15$ 未満の階級にあるので、答えはその階級の階級値である $12.5$ となります。

問題解説(6)

問題${\small (6)}$ $5$ 以上 $10$ 未満の相対度数と $20$ 以上 $25$ 未満の相対度数をそれぞれ求めよ。

度数の合計は $32$ であり、$5$ 以上 $10$ 未満の度数は表より、$8$ であるので、$$~~~\frac{8}{32}=0.25$$
また、$20$ 以上 $25$ 未満の度数は表より、$2$ であるので、$$~~~\frac{2}{32}=0.0625$$
よって、答えは$$~~~0.25~,~0.065$$となります。

今回のまとめ

度数分布表を作るときは、各階級の度数の数え間違えに注意しましょう。また、度数分布表からの代表値の求め方も覚えておきましょう。

【問題一覧】数学Ⅰ：データの分析

このページは「高校数学Ⅰ：データの分析」の問題一覧ページとなります。解説の見たい単元名がわからないと...

以上〜未満	階級値	度数
\(0\) 〜 \(10\)	\(5\)	\(2\)
\(10\) 〜 \(20\)	\(15\)	\(5\)
\(20\) 〜 \(30\)	\(25\)	\(3\)
合計		\(10\)

以上〜未満	度数	相対度数
\(0\) 〜 \(10\)	\(2\)	\(0.2\)
\(10\) 〜 \(20\)	\(5\)	\(0.5\)
\(20\) 〜 \(30\)	\(3\)	\(0.3\)
合計	\(10\)	\(1\)

以上〜未満	階級値	度数	階級値×度数
\(0\) 〜 \(10\)	\(5\)	\(2\)	\(5\times2\)
\(10\) 〜 \(20\)	\(15\)	\(5\)	\(15\times5\)
\(20\) 〜 \(30\)	\(25\)	\(3\)	\(25\times3\)
合計		\(10\)

以上〜未満	度数
\(0\) 〜 \(5\)	\(7\)
\(5\) 〜 \(10\)	\(8\)
\(10\) 〜 \(15\)	\(10\)
\(15\) 〜 \(20\)	\(5\)
\(20\) 〜 \(25\)	\(2\)
合計	\(32\)

以上〜未満	階級値	度数	階級値×度数
\(0\) 〜 \(5\)	\(2.5\)	\(7\)	\(17.5\)
\(5\) 〜 \(10\)	\(7.5\)	\(8\)	\(60\)
\(10\) 〜 \(15\)	\(12.5\)	\(10\)	\(125\)
\(15\) 〜 \(20\)	\(17.5\)	\(5\)	\(87.5\)
\(20\) 〜 \(25\)	\(22.5\)	\(2\)	\(45\)
合計		\(32\)