複素数範囲での2次方程式の解の条件の解法
(ⅰ) \(D>0\)
\(~\Leftrightarrow~\)異なる2つの実数解をもつ
(ⅱ) \(D=0\)
\(~\Leftrightarrow~\)重解をもつ
(ⅲ) \(D<0\)
\(~\Leftrightarrow~\)異なる2つの虚数解をもつ
問題解説:複素数範囲での2次方程式の解の条件
問題解説(1)
\({\small (1)}~\) 次の2次方程式の解の種類を判別せよ。$$~{\large ①}~9x^2-6x+1=0$$$$~{\large ②}~x^2-x-1=0$$$$~{\large ③}~x^2+2x+4=0$$
① \(9x^2-6x+1=0\)
判別式を \(D\) とすると、$$~~~D=(-6)^2-4\cdot9\cdot1$$$$\hspace{ 18 pt}=36-36$$$$\hspace{ 18 pt}=0$$\(D=0\) となるので、この2次方程式は重解をもちます。
② \(x^2-x-1=0\)
判別式を \(D\) とすると、$$~~~D=(-1)^2-4\cdot1\cdot(-1)$$$$\hspace{ 18 pt}=1+4$$$$\hspace{ 18 pt}=5$$\(D>0\) となるので、この2次方程式は異なる2つの実数解をもちます。
③ \(x^2+2x+4=0\)
判別式を \(D\) とすると、$$~~~D=2^2-4\cdot1\cdot4$$$$\hspace{ 18 pt}=4-16$$$$\hspace{ 18 pt}=-12$$\(D<0\) となるので、この2次方程式は異なる2つの虚数解をもちます。
問題解説(2)
\({\small (2)}~\) 2次方程式 \(x^2-kx+1=0\) の解の種類を判別せよ。ただし、\(k\) は定数とする。
この2次方程式の判別式を \(D\) とすると、$$~~~D=(-k)^2-4\cdot1\cdot1$$$$\hspace{ 18 pt}=k^2-4$$$$\hspace{ 18 pt}=(k+2)(k-2)$$
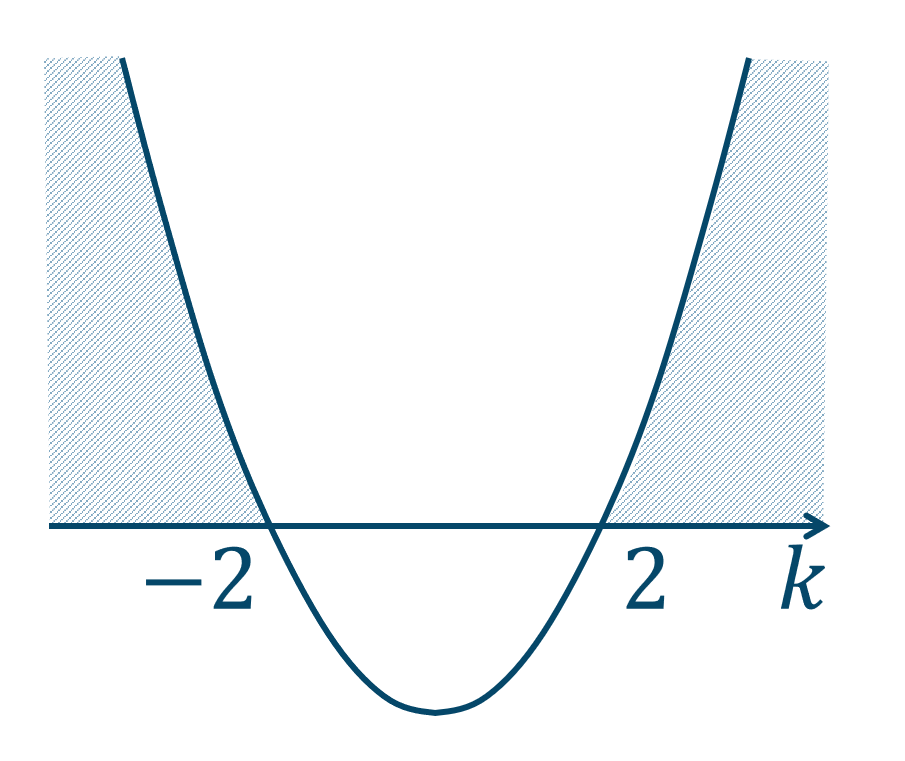
(ⅰ) \(D>0\) のとき$$~~~D=(k+2)(k-2)>0$$
グラフより、\(k<-2~,~2<k\)
このとき、異なる2つの実数解をもちます。
(ⅱ) \(D=0\) のとき$$~~~D=(k+2)(k-2)=0$$$$\hspace{ 10 pt}k=\pm2$$このとき、重解をもちます。
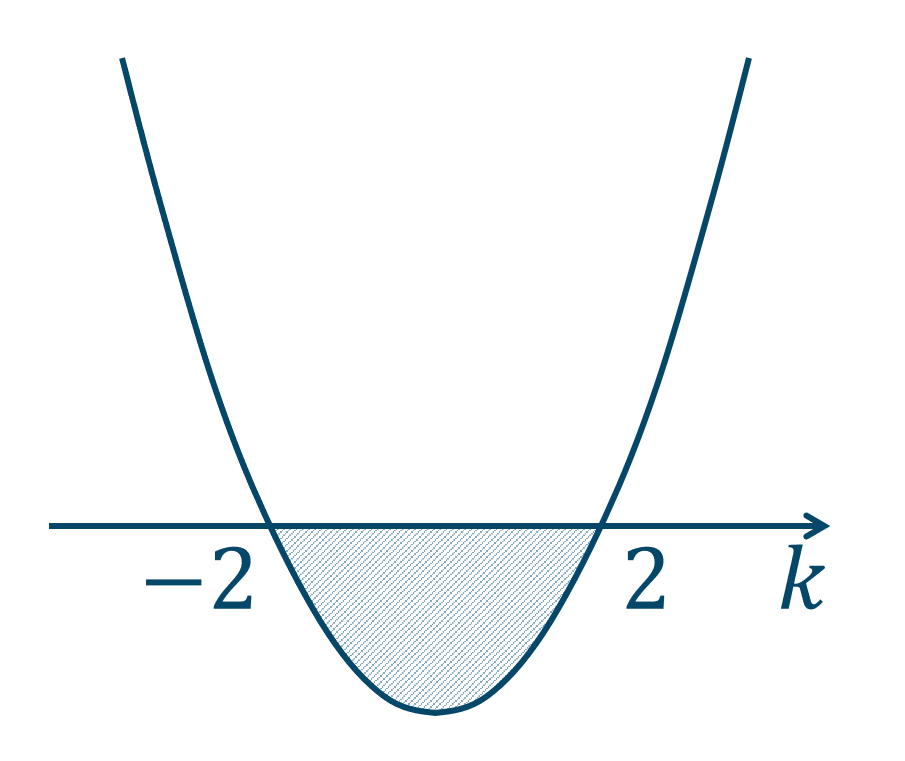
(ⅲ) \(D<0\) のとき$$~~~D=(k+2)(k-2)<0$$
グラフより、\(-2<k<2\)
このとき、異なる2つの虚数解をもちます。
したがって、この2次方程式は、$$~~~k<-2~,~2<k$$このとき、異なる2つの実数解をもちます。$$~~~k=\pm2$$このとき、重解をもちます。$$~~~-2<k<2$$このとき、2つの虚数解をもちます。
今回のまとめ
2次方程式の解の種類の判別はどのようなときでも判別式が使えます。3つの場合を覚えておきましょう。