三角関数のグラフの式変形
\(y=\sin{\theta}\) のグラフを \(\theta\) 軸方向に \({\Large \frac{1}{b}}\) 倍して、\(\theta\) 軸方向に \(+p\) 平行移動したグラフとなります。
この式は( )の中の \(\theta\) の係数が \(1\) となっていることがポイントです。まずはこの式に式変形しましょう。
問題解説:三角関数のグラフ⑤(式変形)
問題解説(1)
$$\hspace{ 10 pt}y=\sin{\left( \frac{1}{2}\theta-\frac{\pi}{6} \right)}$$\({\Large \frac{1}{2}}\) でくくると、$$\hspace{ 10 pt}y=\sin\frac{1}{2}{\left( \theta-\frac{\pi}{3} \right)}$$よって、この関数のグラフは、\(y=\sin{\theta}\) のグラフを \(\theta\) 軸方向に \(2\) 倍して、\(\theta\) 軸方向に \(+{\Large \frac{\pi}{3}}\) 平行移動したグラフとなります。
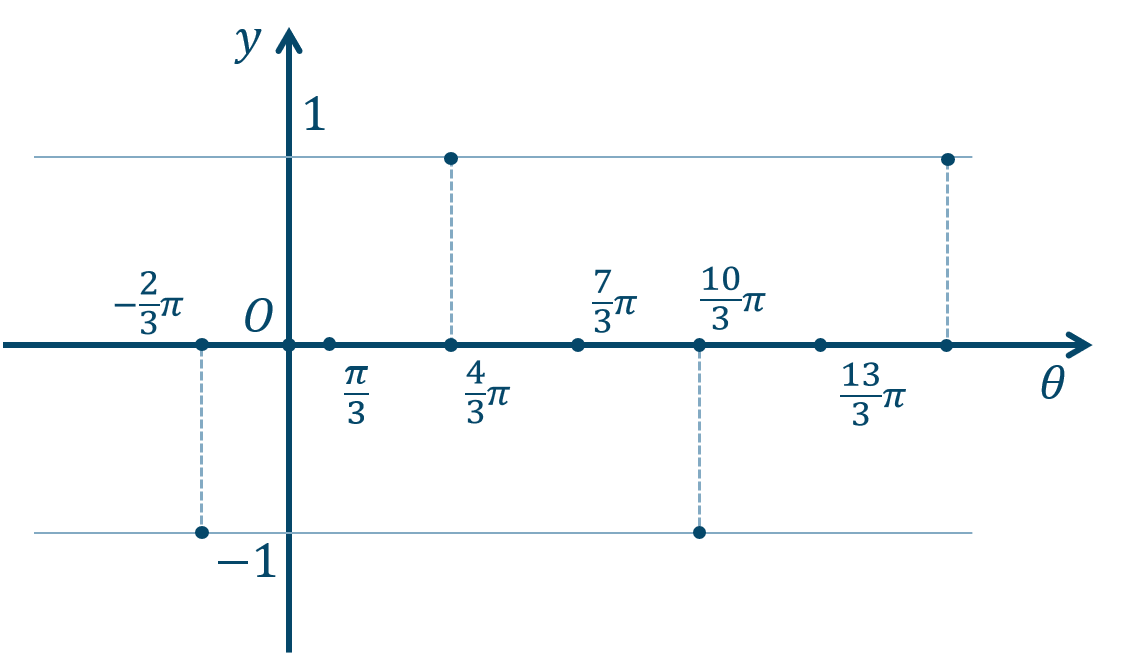
① 通る点などを書き込んでいきます。
\(y=\sin{\theta}\) での \(\theta\) 軸上の点や \(y=\pm1\) となる点は、$$~~~-\frac{\pi}{2}~,~0~,~\frac{\pi}{2}~,~\pi~,~\frac{3}{2}\pi~,~2\pi~,~\cdots$$となりますが、それぞれ \(2\) 倍の位置となるので、$$~~~-\pi~,~0~,~\pi~,~2\pi~,~3\pi~,~4\pi~,~\cdots$$となります。
さらに \(\theta\) 軸方向に \(+{\Large \frac{\pi}{3}}\) 平行移動するので、$$~~~-\frac{2}{3}\pi~,~\frac{\pi}{3}~,~\frac{4}{3}\pi~,~\frac{7}{3}\pi~,~\frac{10}{3}\pi~,~\frac{13}{3}\pi~,~\cdots$$となります。
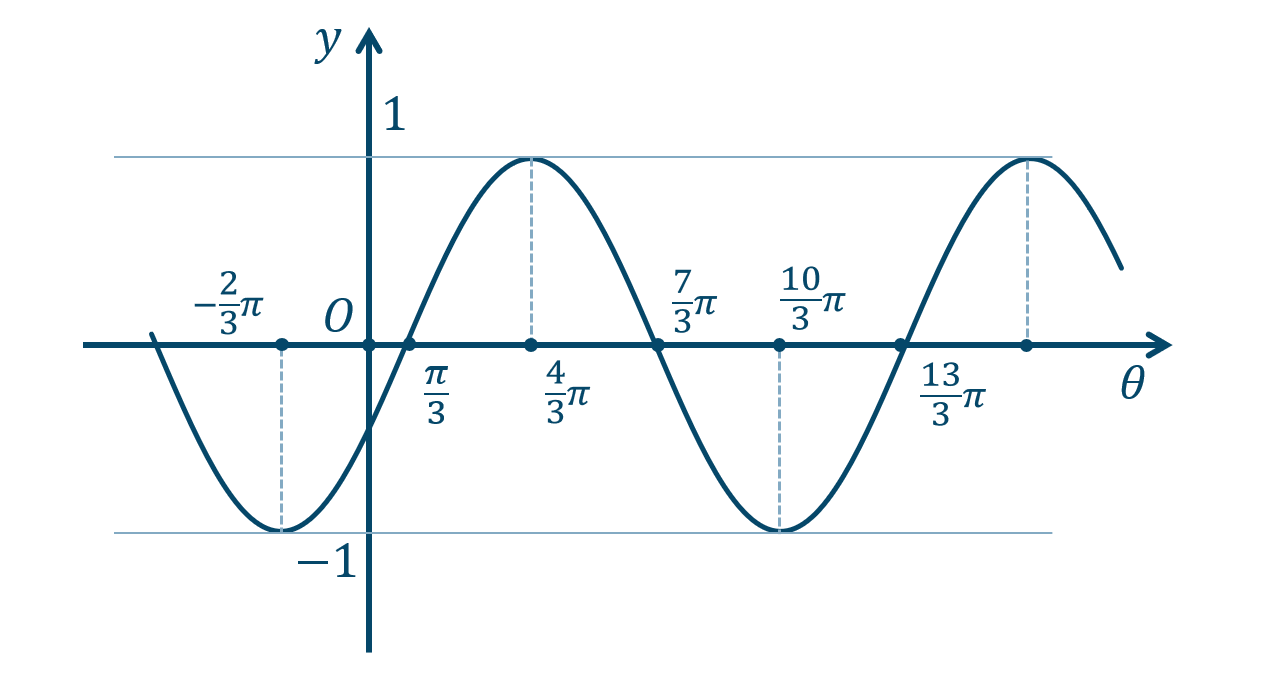
② 点を曲線で結びます。また、点の座標や、\(y=\pm1\) の線を書き込みます。
また、周期も\(2\) 倍となるので、 \(4\pi\) となります。
問題解説(2)
$$\hspace{ 10 pt} y=\cos{(2\theta+\pi)}$$\(2\) でくくると、$$\hspace{ 10 pt} y=\cos{2\left(\theta+\frac{\pi}{2}\right)}$$よって、この関数のグラフは、\(y=\cos{\theta}\) のグラフを \(\theta\) 軸方向に \({\Large \frac{1}{2}}\) 倍して、\(\theta\) 軸方向に \(-{\Large \frac{\pi}{2}}\) 平行移動したグラフとなります。
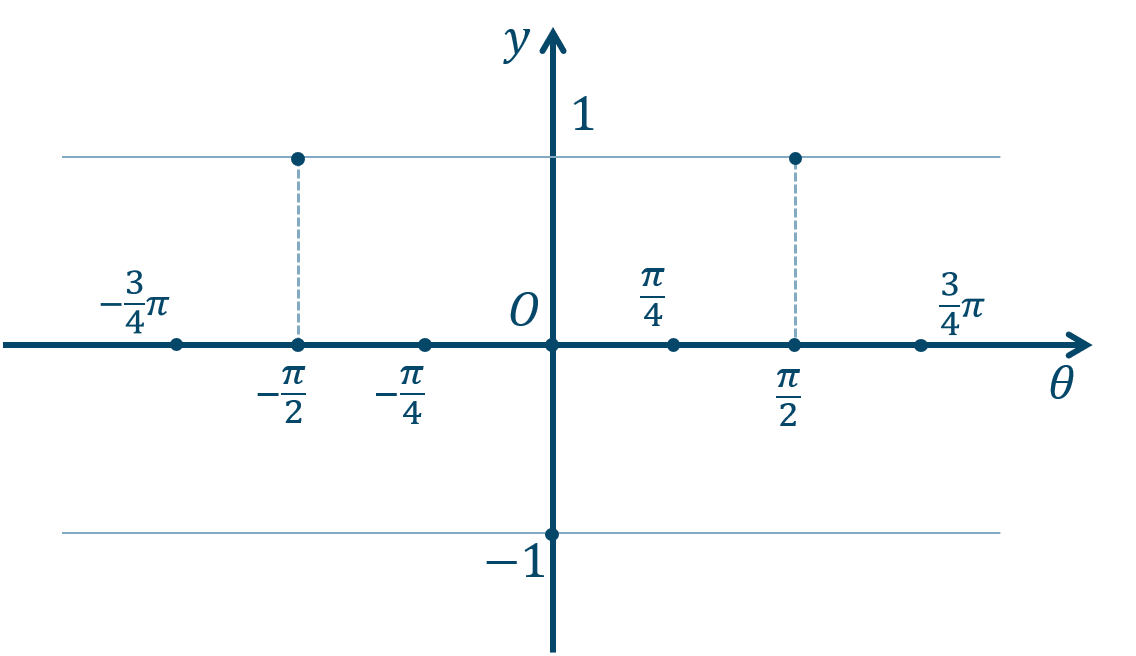
① 通る点などを書き込んでいきます。
\(y=\cos{\theta}\) での \(\theta\) 軸上の点や \(y=\pm1\) となる点は、$$~~~-\frac{\pi}{2}~,~0~,~\frac{\pi}{2}~,~\pi~,~\frac{3}{2}\pi~,~2\pi~,~\cdots$$となりますが、それぞれ \({\Large \frac{1}{2}}\) 倍の位置となるので、$$~~~-\frac{\pi}{4}~,~0~,~\frac{\pi}{4}~,~\frac{\pi}{2}~,~\frac{3}{4}\pi~,~\pi~,~\cdots$$これらの点を書き込みます。
さらに \(\theta\) 軸方向に \(-{\Large \frac{\pi}{2}}\) 平行移動するので、$$~~~-\frac{3}{4}\pi~,~-\frac{\pi}{2}~,~-\frac{\pi}{4}~,~0~,~\frac{\pi}{4}~,~\frac{3}{4}\pi~,~\cdots$$となります。
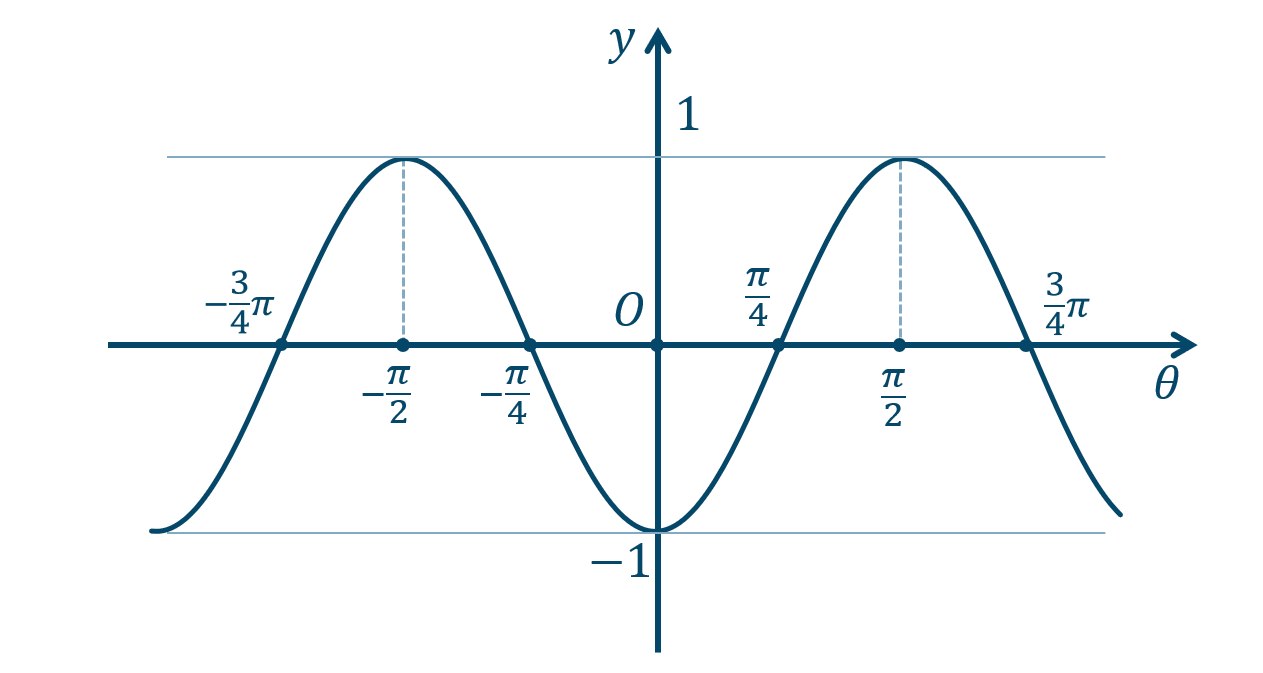
② 点を曲線で結びます。また、点の座標や、\(y=\pm1\) の線を書き込みます。
また、周期も\({\Large \frac{1}{2}}\) 倍となるので、 \(\pi\) となります。
今回のまとめ
式変形が必要な三角関数のグラフは、まず \(\theta\) の係数が \(1\) となるようにくくって式変形を覚えておきましょう。また、グラフを描くときは先に通る点を書き込んでいきましょう。