三角関数を含む方程式
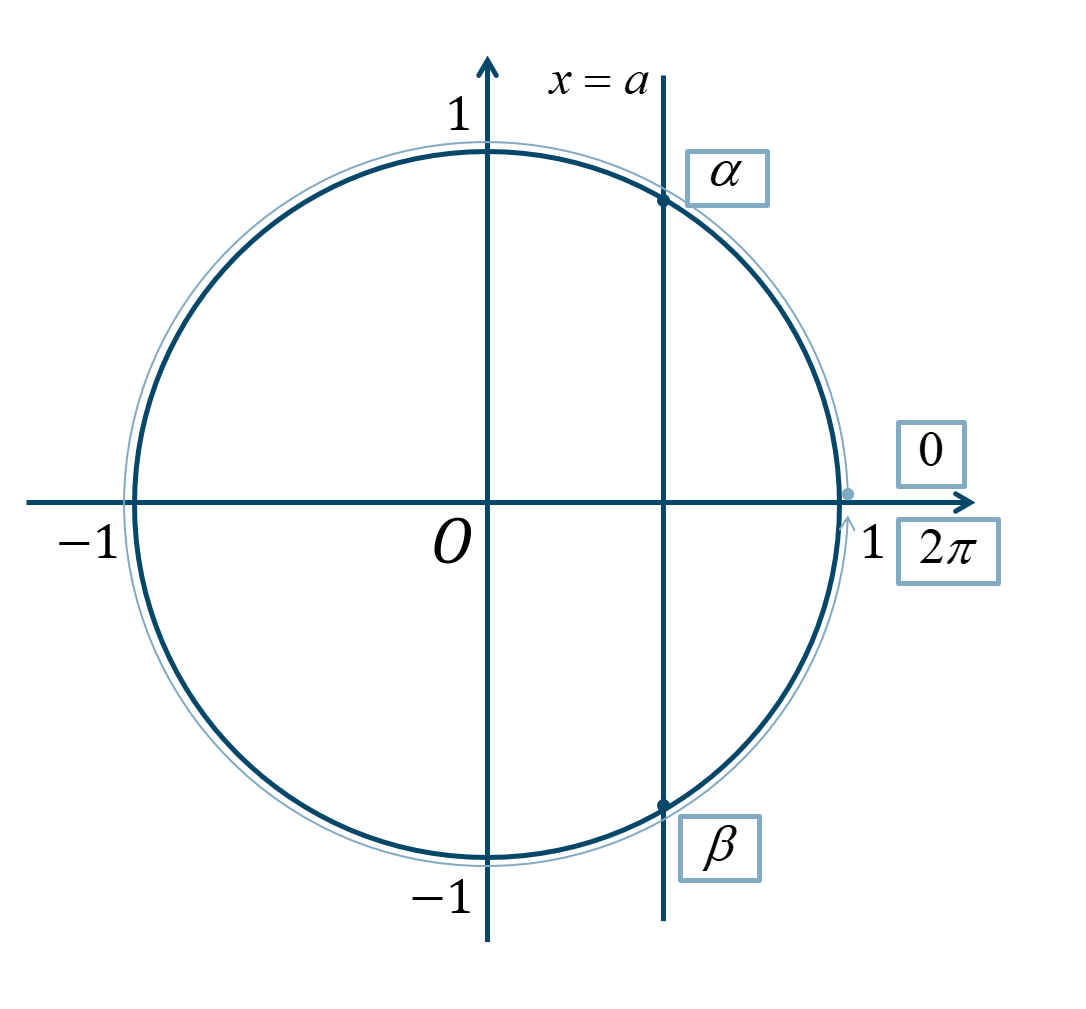
\(x\) 座標が \(a\) となればよいので、単位円上に \(x=a\) の直線を描きます。この交点のときの角が答えとなります。
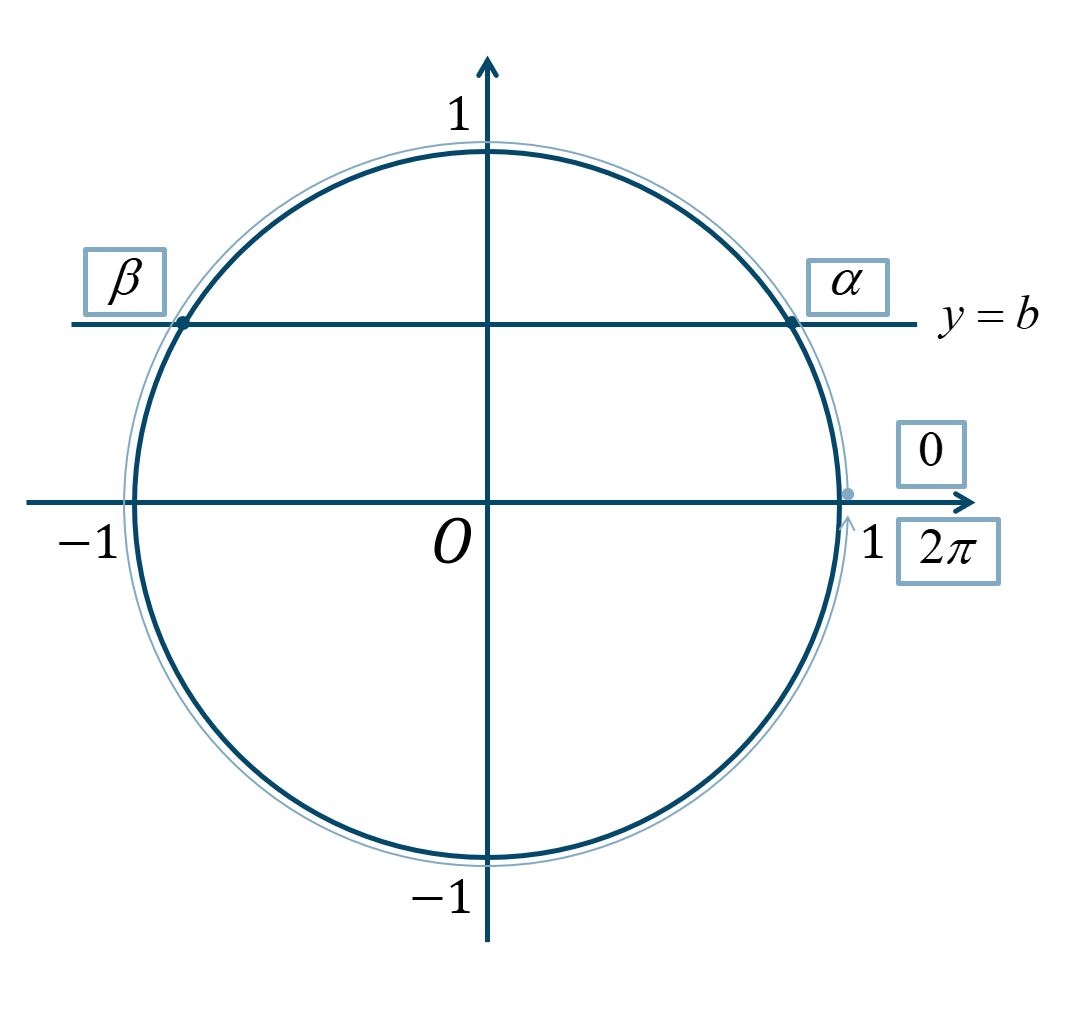
② \(\sin{\theta}=b\)
\(y\) 座標が \(b\) となればよいので、単位円上に \(y=b\) の直線を描きます。この交点のときの角が答えとなります。
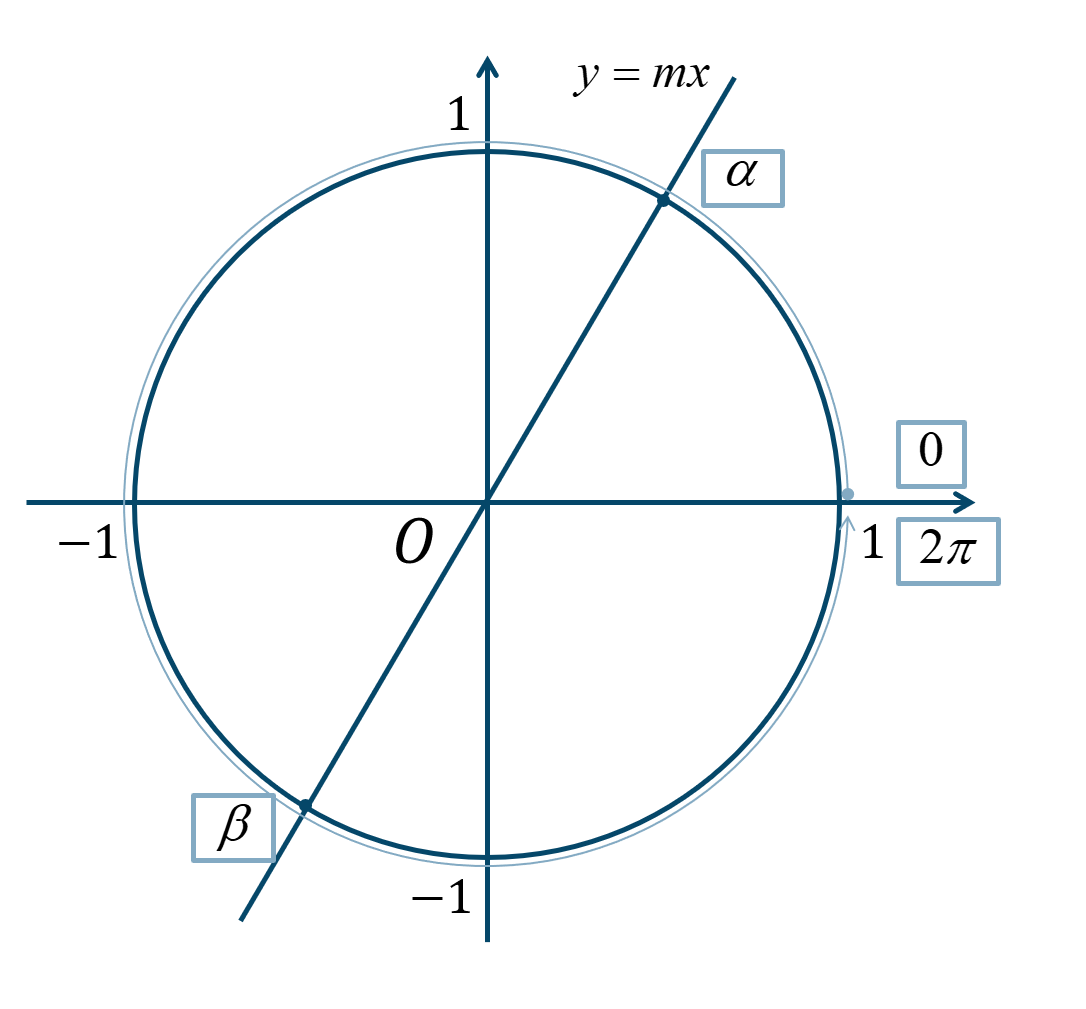
③ \(\tan{\theta}=m\)
傾きが \(m\) となればよいので、単位円上に \(y=mx\) の直線を描きます。この交点のときの角が答えとなります。

問題解説:三角関数を含む方程式①
問題解説(1)
ただし、\(0≦\theta<2\pi\) とする。$${\small (1)}~\sin{\theta}=-\frac{\sqrt{3}}{2}$$
直線 \(y=-{\Large \frac{\sqrt{3}}{2}}\) と単位円との交点より、

\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{6}}\) が8個分と10個分のときとなるので、$$~~~\theta=\frac{8}{6}\pi=\frac{4}{3}\pi$$また、$$~~~\theta=\frac{10}{6}\pi=\frac{5}{3}\pi$$
よって、答えは、$$~~~\theta=\frac{4}{3}\pi~,~\frac{5}{3}\pi$$となります。
問題解説(2)
ただし、\(0≦\theta<2\pi\) とする。$${\small (2)}~\sqrt{2} \cos{\theta}-1=0$$
この式を式変形すると、$$\hspace{ 10 pt}\sqrt{2}\cos{\theta}-1=0$$移項して、\(\sqrt{2}\) で割ると、$$\hspace{ 10 pt}\sqrt{2}\cos{\theta}=1$$$$\hspace{ 26 pt}\cos{\theta}=\frac{1}{\sqrt{2}}$$
直線 \(x={\Large \frac{1}{\sqrt{2}}}\) と単位円との交点より、

\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{4}}\) が1個分と7個分のときとなるので、答えは、$$~~~\theta=\frac{\pi}{4}~,~\frac{7}{4}\pi$$となります。
問題解説(3)
ただし、\(0≦\theta<2\pi\) とする。$${\small (3)}~\tan{\theta}+1=0$$
この式を式変形すると、$$\hspace{ 10 pt}\tan{\theta}+1=0$$移項すると、$$\hspace{ 10 pt}\tan{\theta}=-1$$
直線 \(y=-x\) と単位円との交点より、
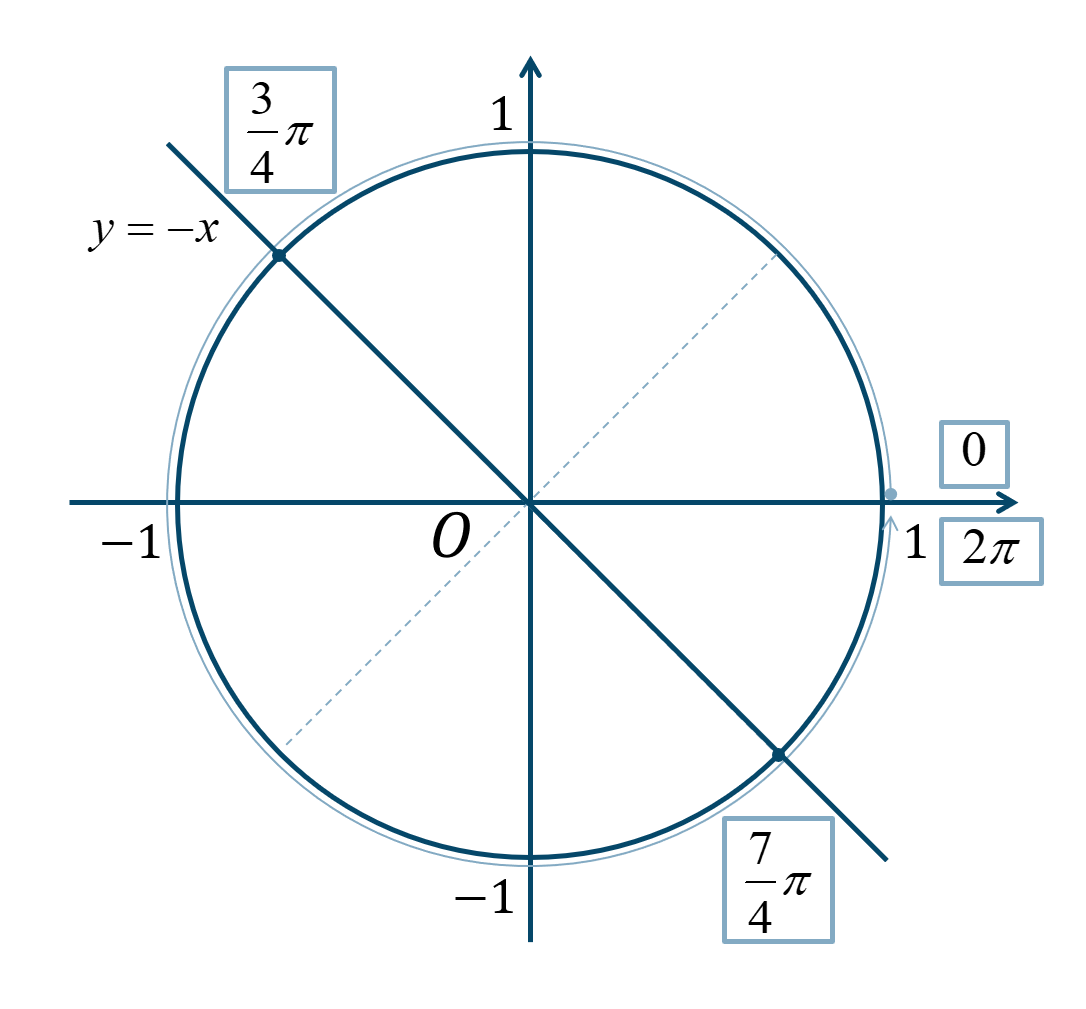
\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{4}}\) が3個分と7個分のときとなるので、答えは、$$~~~\theta=\frac{3}{4}\pi~,~\frac{7}{4}\pi$$となります。
今回のまとめ
三角関数を含む方程式より角を求める問題は単位円より求めましょう。重要な問題となりますので、問題演習ページで練習しておきましょう。





