今回の問題は「【問題演習】三角関数を含む方程式」です。

問題演習
[ 解答を見る ]
次の単位円より、
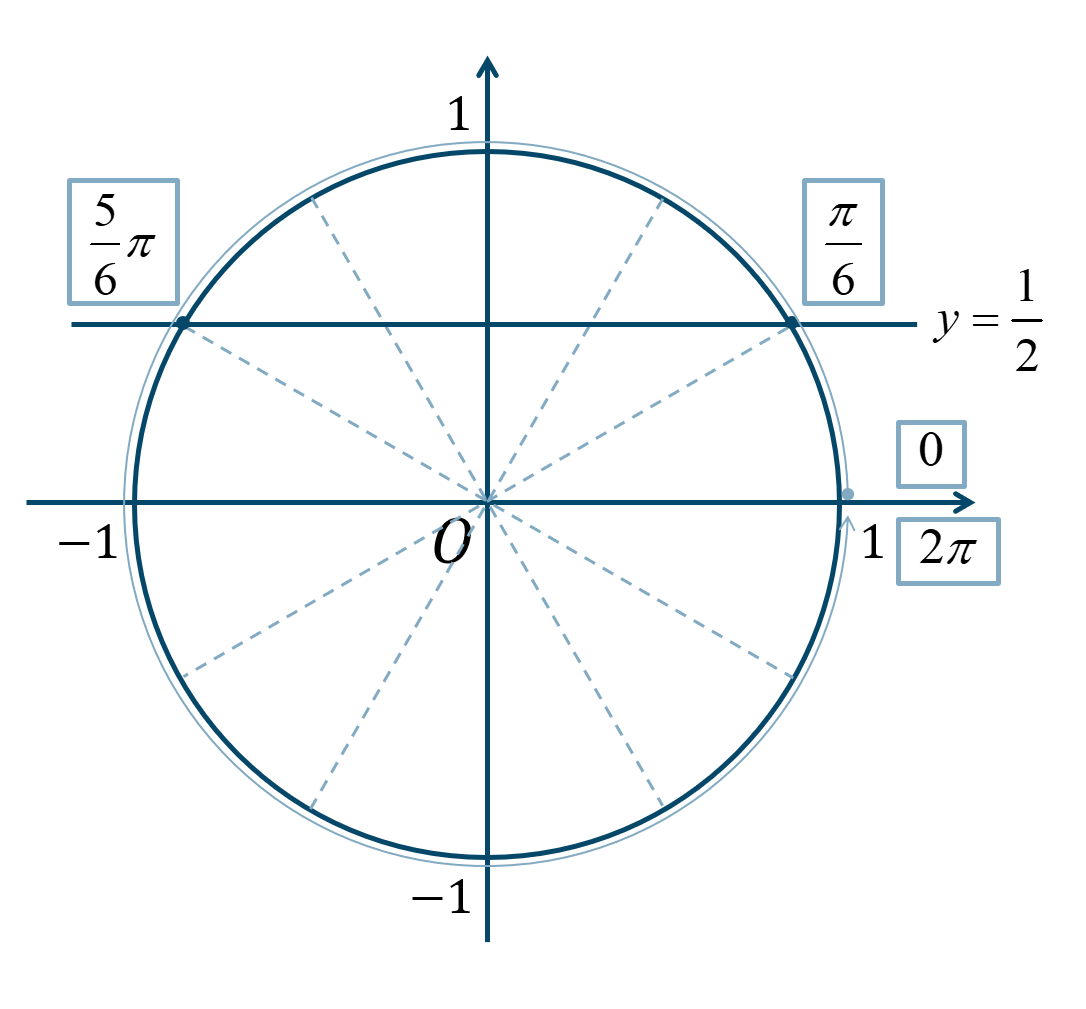
\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{6}}\) が1個分と5個分となります。
よって、答えは$$~~~\theta=\frac{\pi}{6}~,~\frac{5}{6}\pi$$となります。
[ 解答を見る ]
次の単位円より、

\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{6}}\) が4個分と8個分となります。
よって、答えは$$~~~\theta=\frac{2}{3}\pi~,~\frac{4}{3}\pi$$となります。
[ 解答を見る ]
次の単位円より、
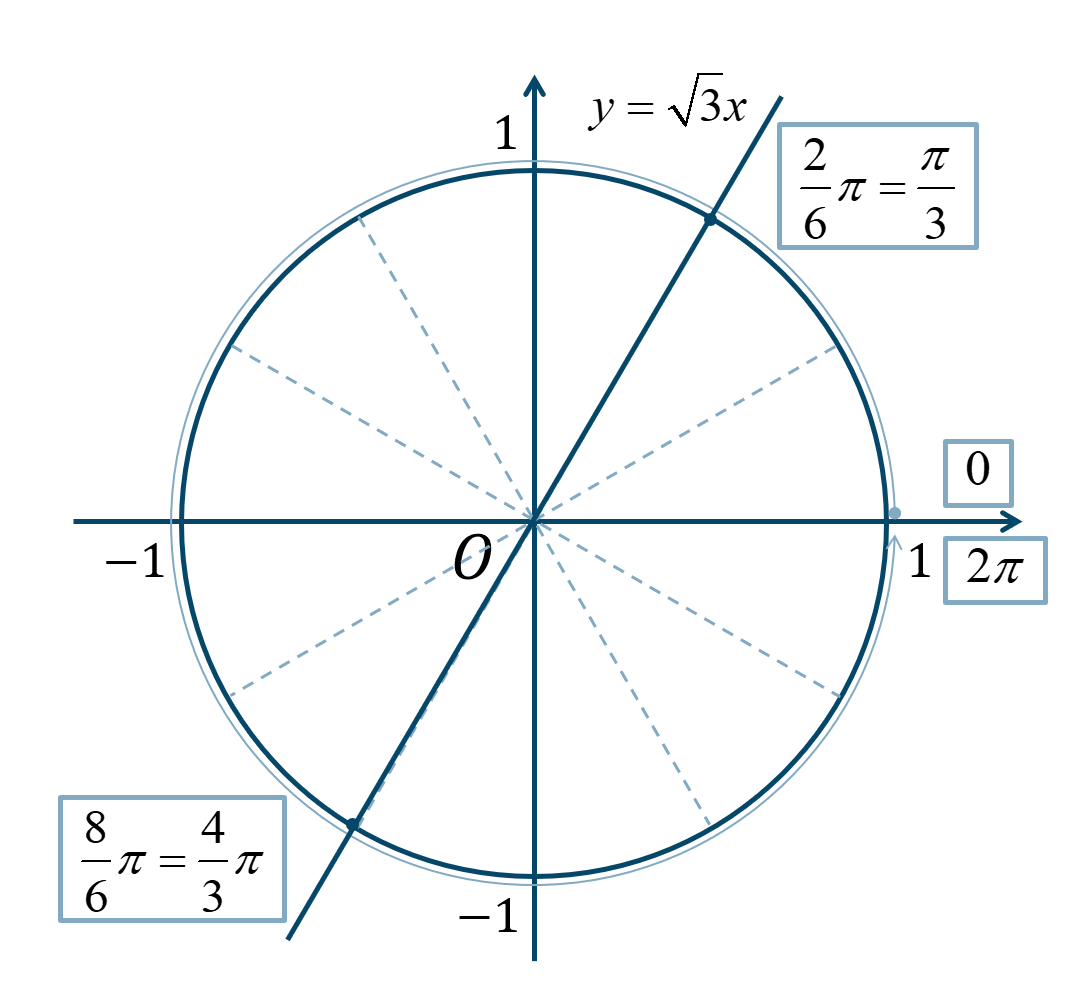
\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{6}}\) が2個分と8個分となります。
よって、答えは$$~~~\theta=\frac{\pi}{3}~,~\frac{4}{3}\pi$$となります。
[ 解答を見る ]
次の単位円より、
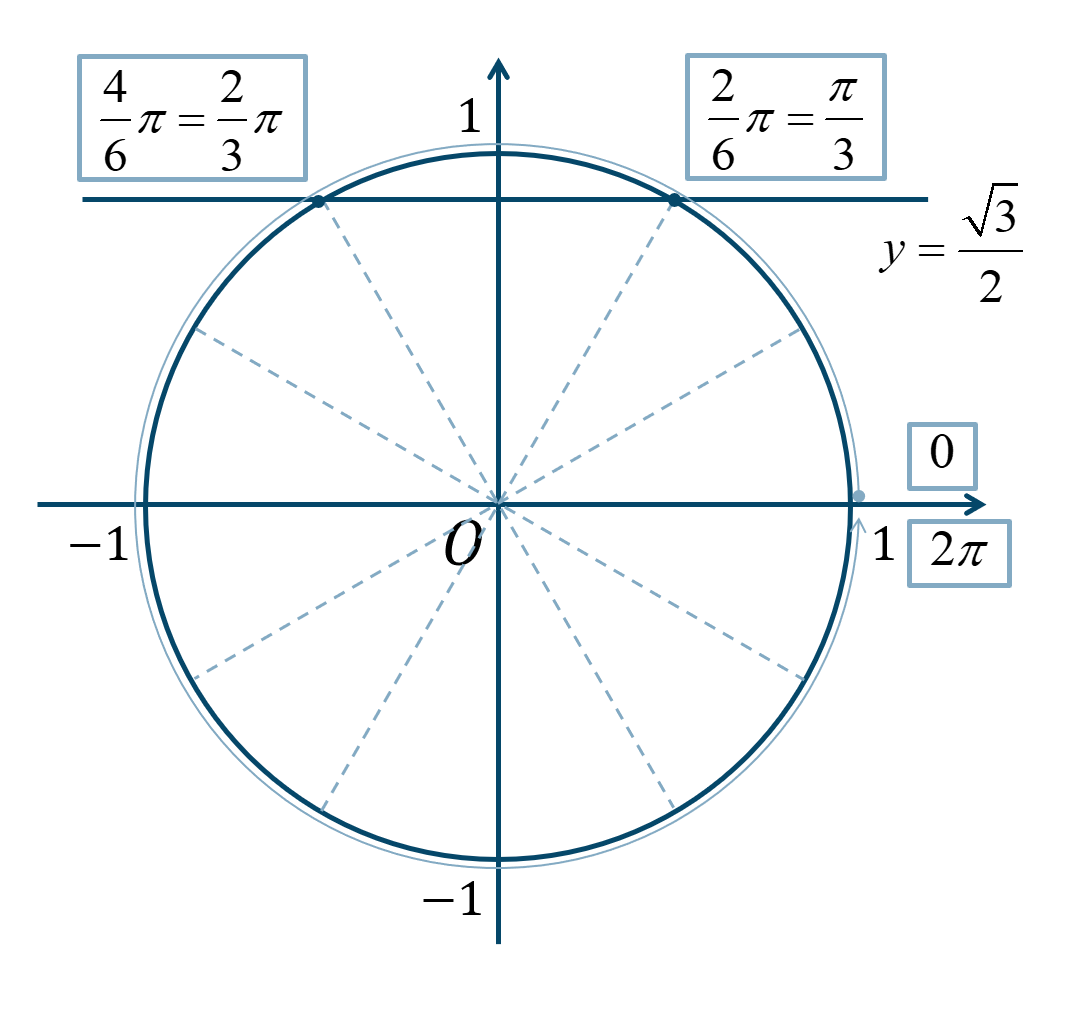
\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{6}}\) が2個分と4個分となります。
よって、答えは$$~~~\theta=\frac{\pi}{3}~,~\frac{2}{3}\pi$$となります。
[ 解答を見る ]
次の単位円より、
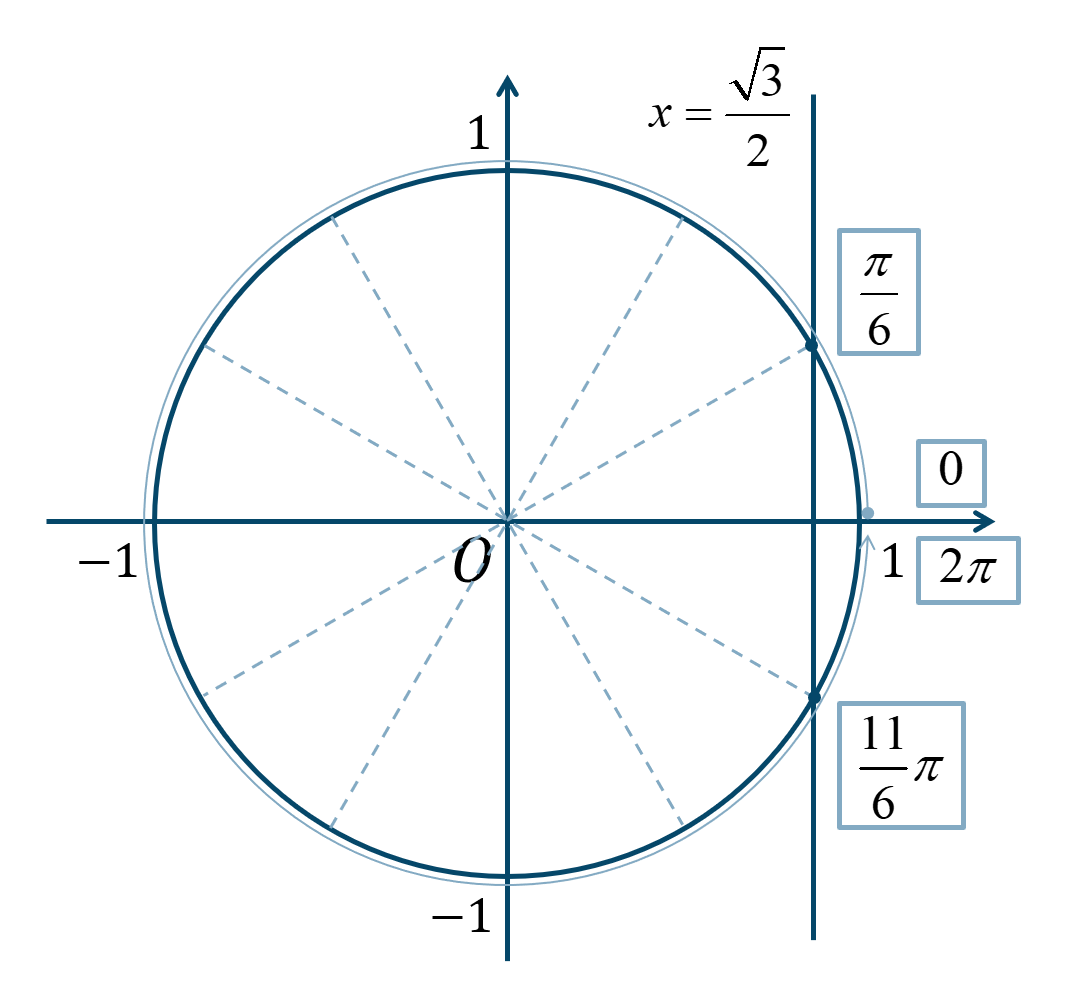
\(0≦x<2\pi\) の範囲で、\({\Large \frac{\pi}{6}}\) が1個分と11個分となります。
よって、答えは$$~~~\theta=\frac{\pi}{6}~,~\frac{11}{6}\pi$$となります。
[ 解答を見る ]
次の単位円より、
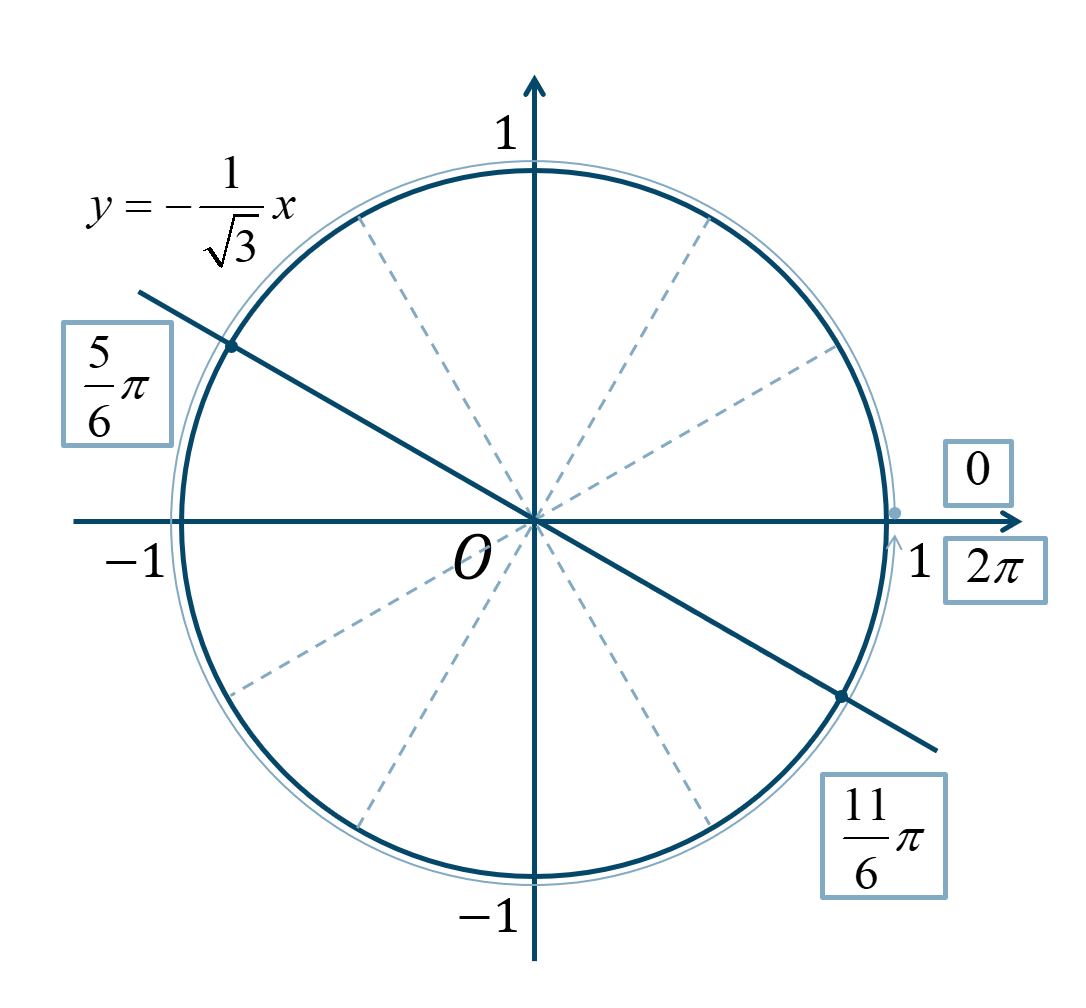
\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{6}}\) が5個分と11個分となります。
よって、答えは$$~~~\theta=\frac{5}{6}\pi~,~\frac{11}{6}\pi$$となります。
[ 解答を見る ]
次の単位円より、
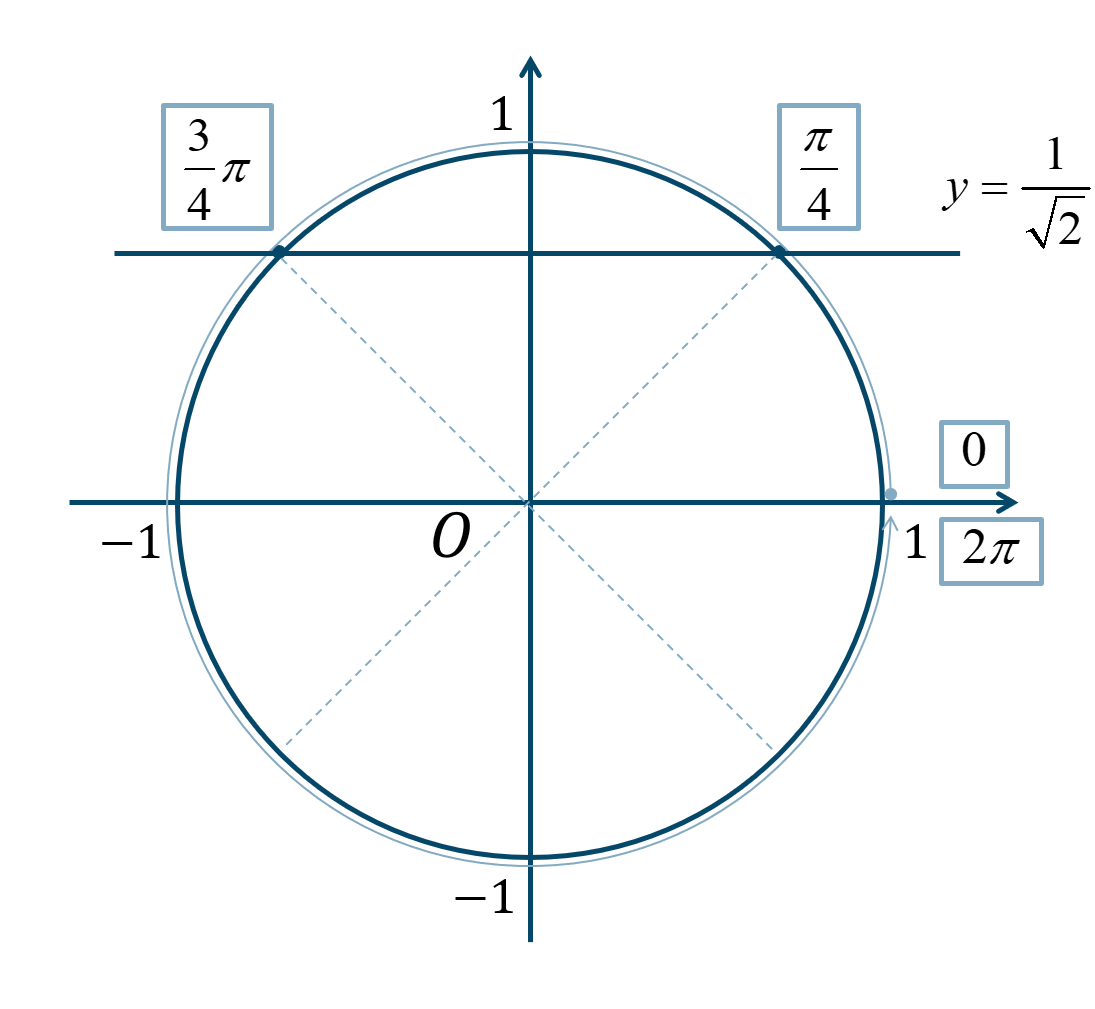
\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{4}}\) が1個分と3個分となります。
よって、答えは$$~~~\theta=\frac{\pi}{4}~,~\frac{3}{4}\pi$$となります。
[ 解答を見る ]
次の単位円より、
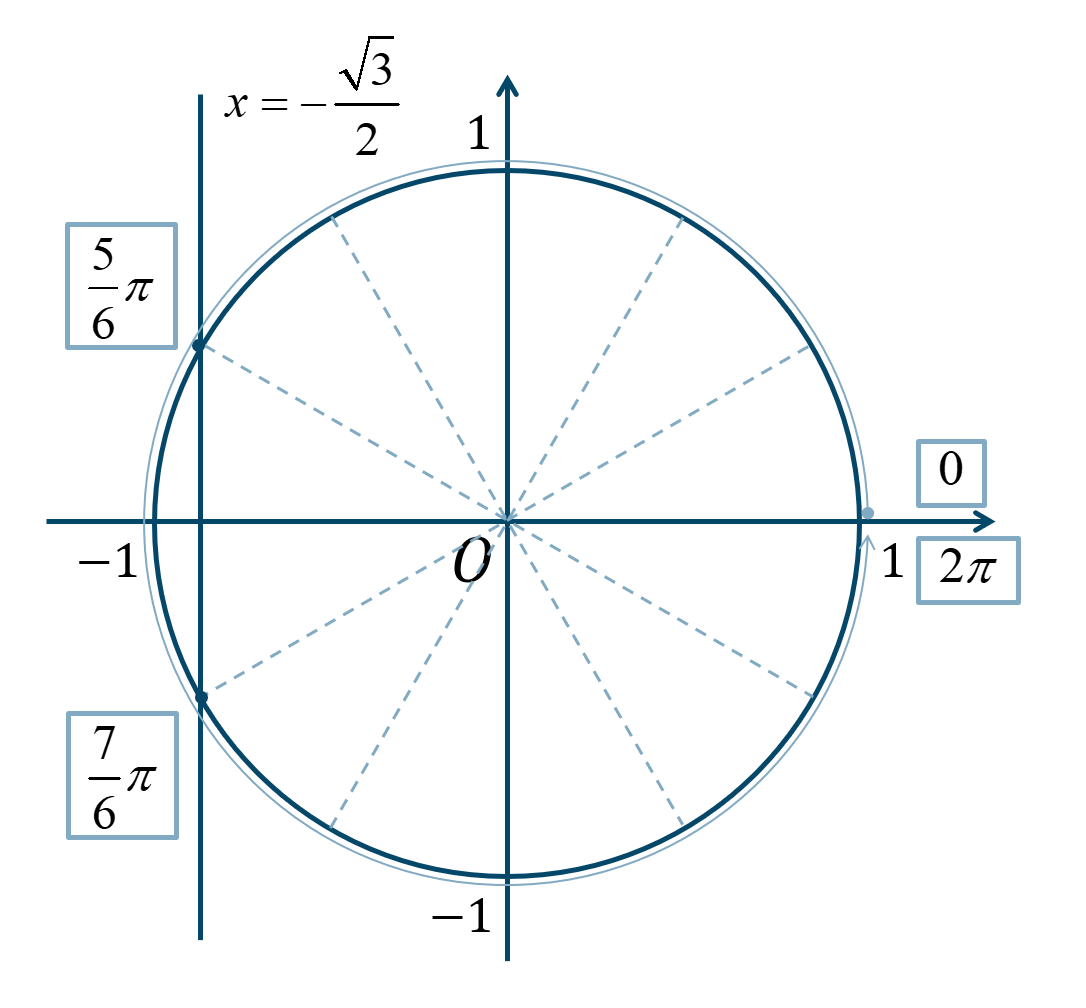
\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{6}}\) が5個分と7個分となります。
よって、答えは$$~~~\theta=\frac{5}{6}\pi~,~\frac{7}{6}\pi$$となります。
[ 解答を見る ]
次の単位円より、
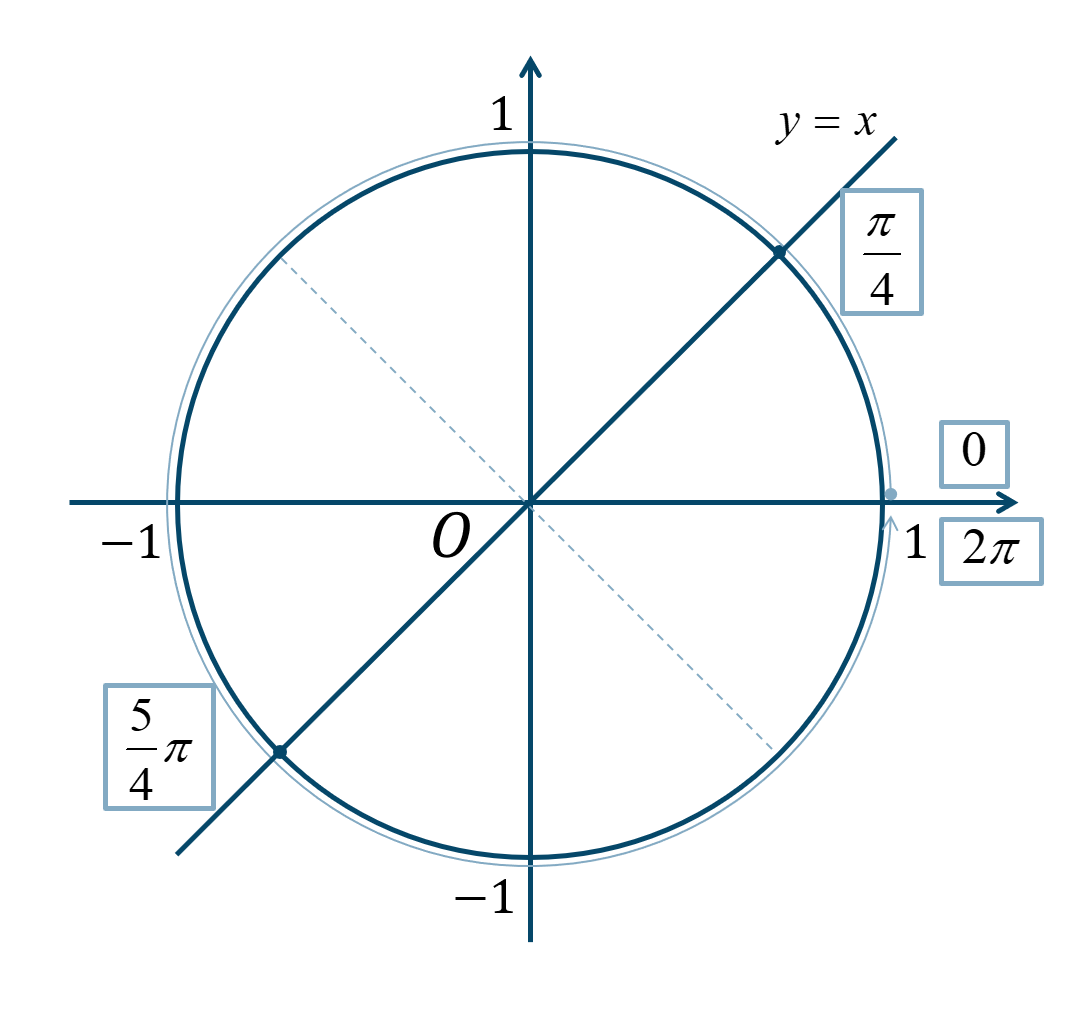
\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{4}}\) が1個分と5個分となります。
よって、答えは$$~~~\theta=\frac{\pi}{4}~,~\frac{5}{4}\pi$$となります。
[ 解答を見る ]
次の単位円より、
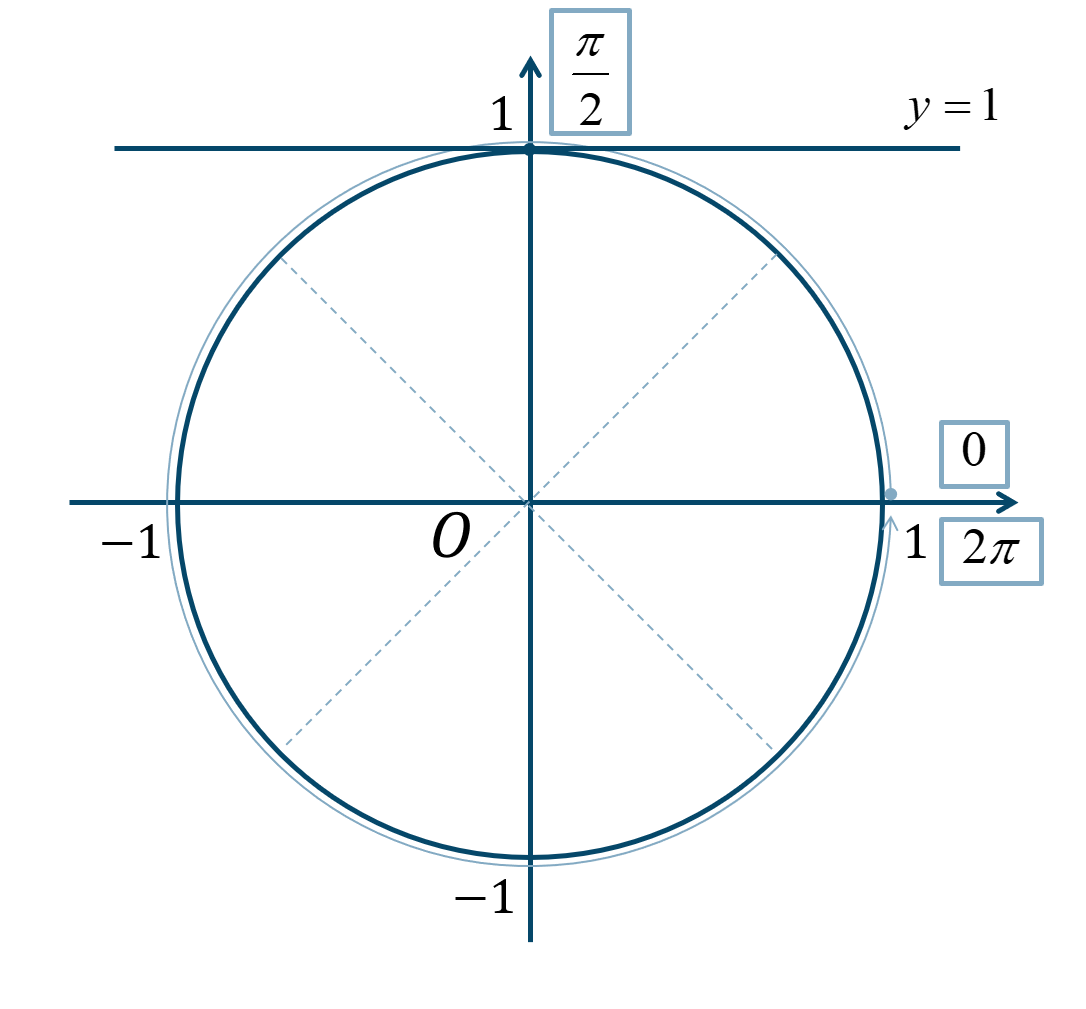
\(0≦\theta<2\pi\) の範囲で考えると、答えは$$~~~\theta=\frac{\pi}{2}$$となります。
[ 解答を見る ]
次の単位円より、

\(0≦\theta<2\pi\) の範囲で考えると、答えは$$~~~\theta=\frac{\pi}{2}~,~\frac{3}{2}\pi$$となります。
[ 解答を見る ]
次の単位円より、
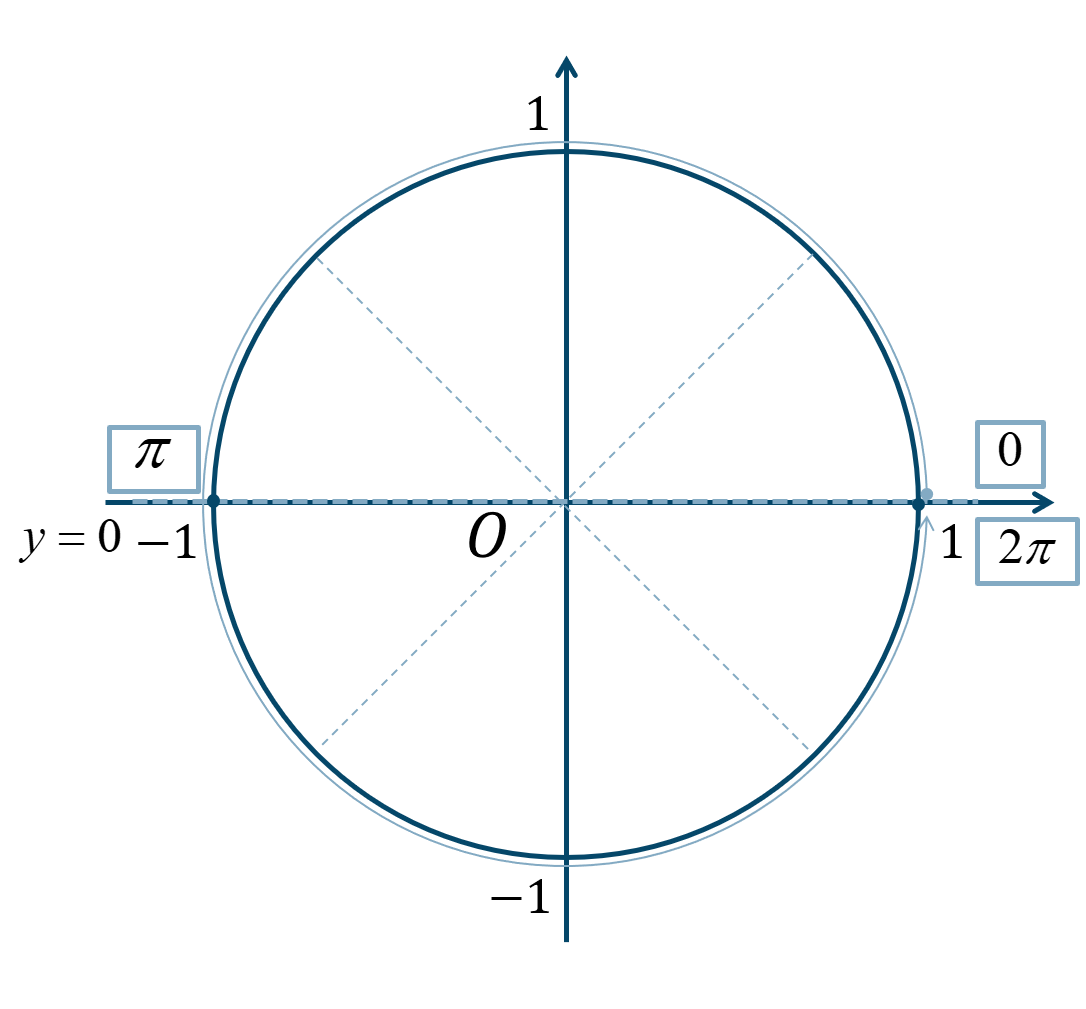
\(0≦\theta<2\pi\) の範囲で考えると、答えは$$~~~\theta=0~,~\pi$$となります。
[ 解答を見る ]
次の単位円より、
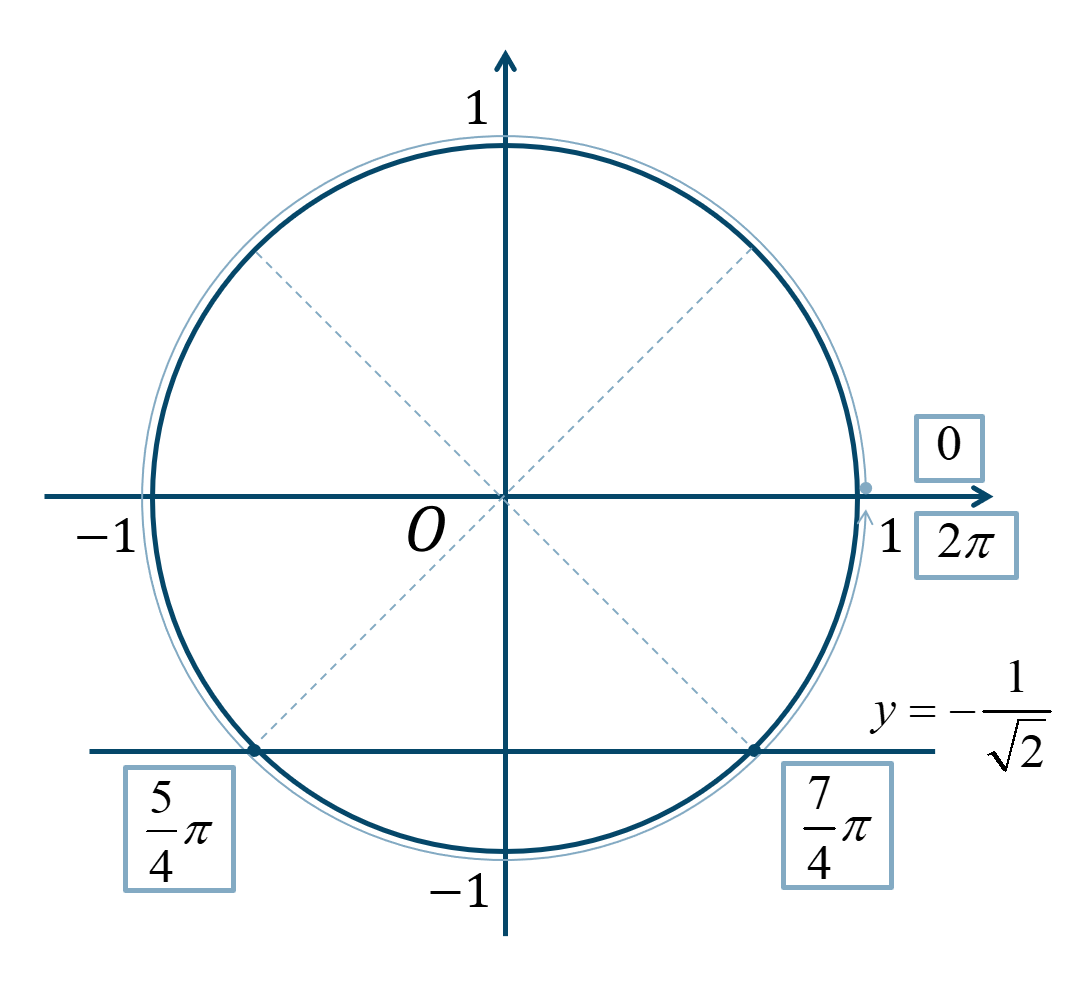
\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{4}}\) が5個分と7個分となります。
よって、答えは$$~~~\theta=\frac{5}{4}\pi~,~\frac{7}{4}\pi$$となります。
[ 解答を見る ]
次の単位円より、
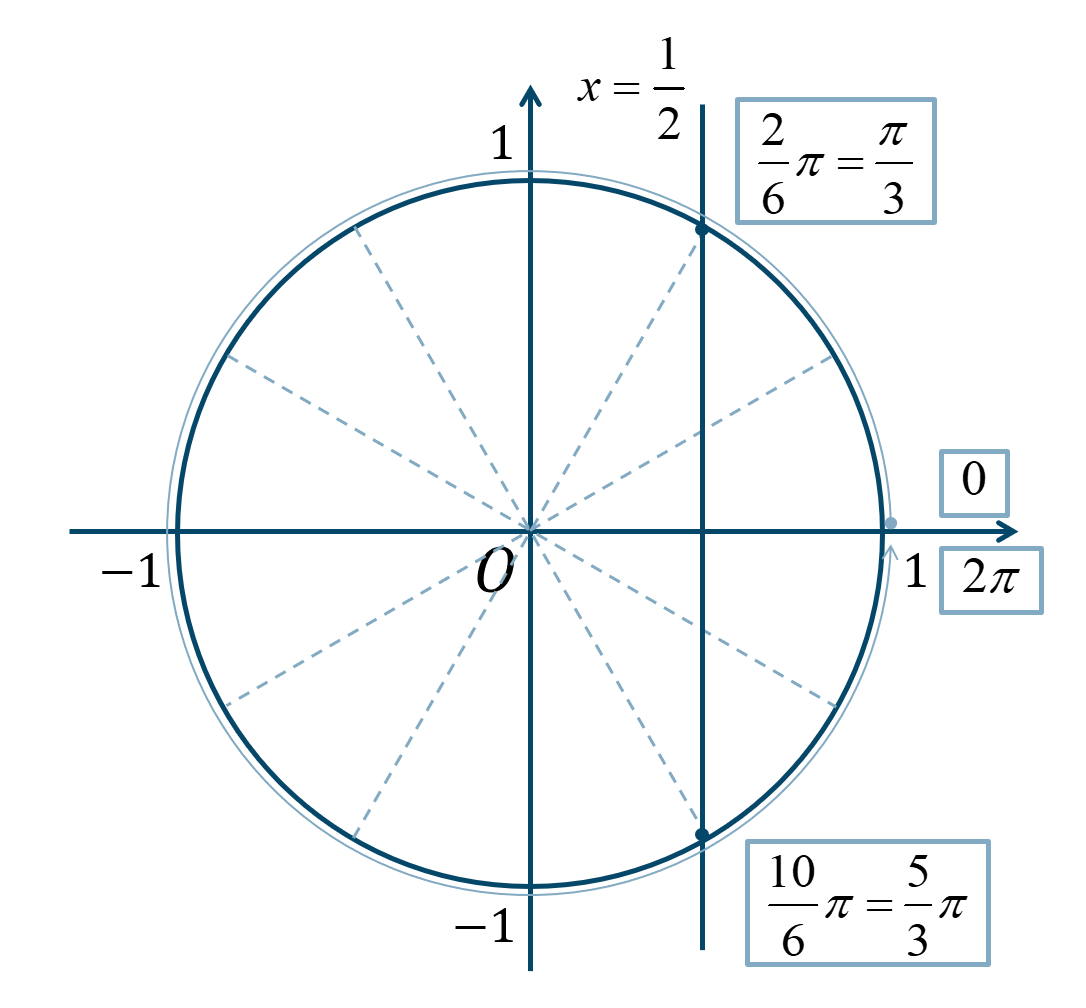
\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{6}}\) が2個分と10個分となります。
よって、答えは$$~~~\theta=\frac{\pi}{3}~,~\frac{5}{3}\pi$$となります。
[ 解答を見る ]
次の単位円より、
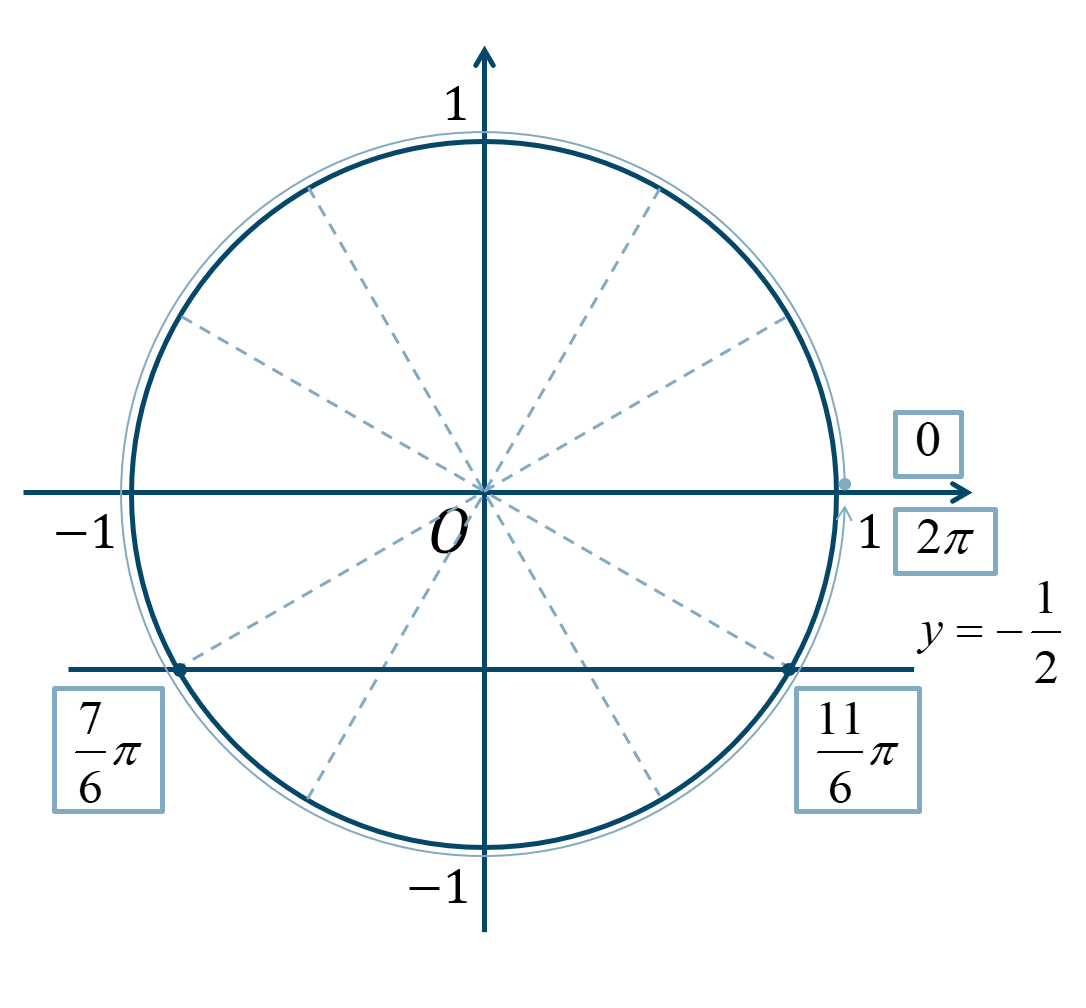
\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{6}}\) が7個分と11個分となります。
よって、答えは$$~~~\theta=\frac{7}{6}\pi~,~\frac{11}{6}\pi$$となります。
[ 解答を見る ]
次の単位円より、
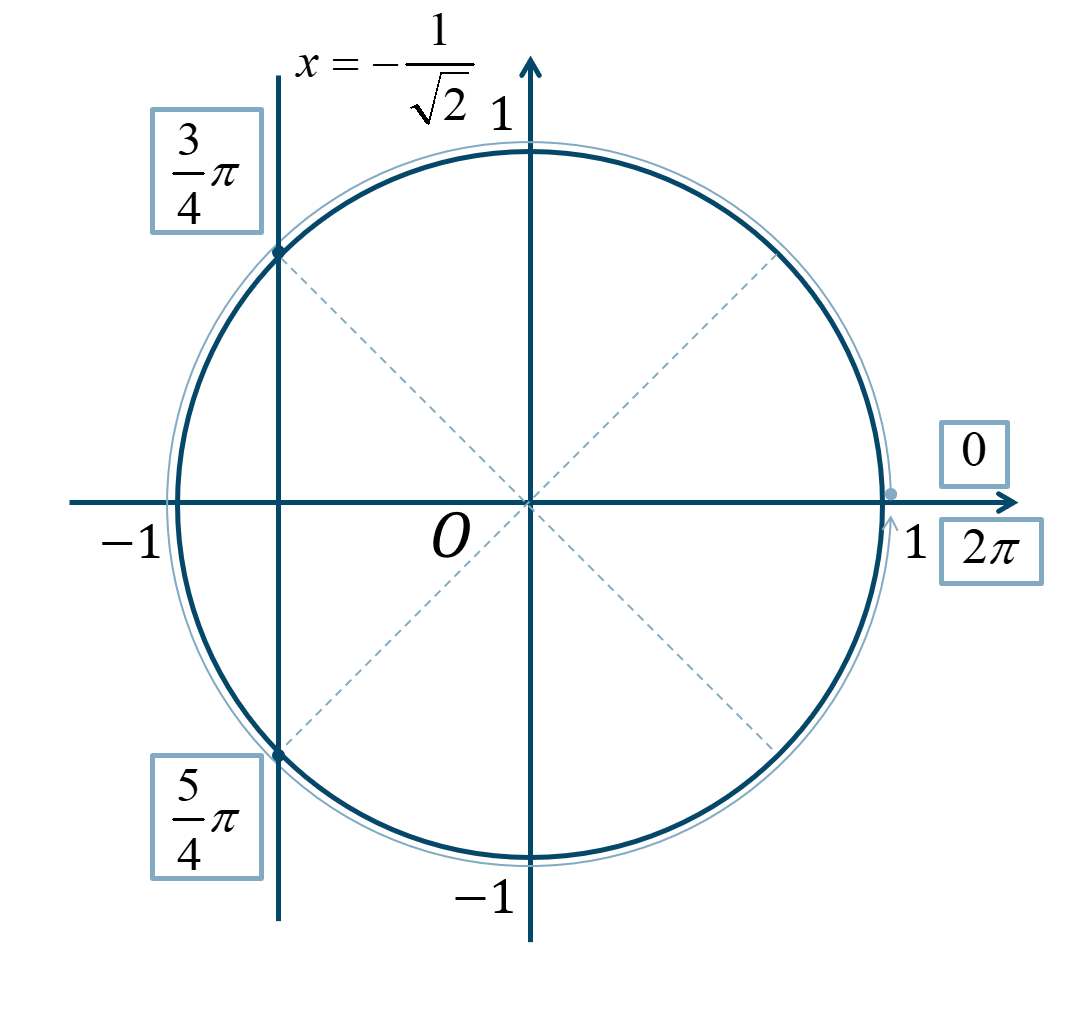
\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{4}}\) が3個分と5個分となります。
よって、答えは$$~~~\theta=\frac{3}{4}\pi~,~\frac{5}{4}\pi$$となります。
[ 解答を見る ]
次の単位円より、
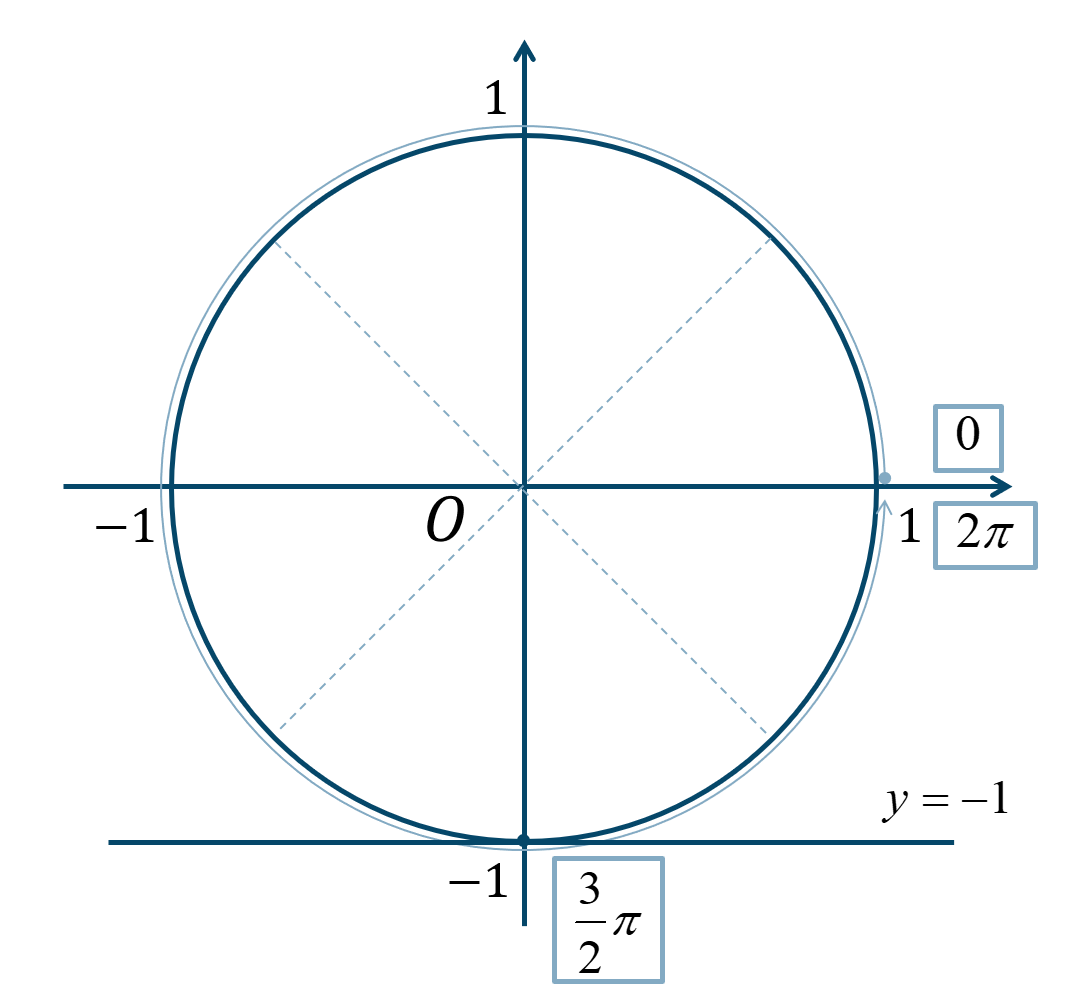
\(0≦\theta<2\pi\) の範囲で考えると、答えは$$~~~\theta=\frac{3}{2}\pi$$となります。
[ 解答を見る ]
次の単位円より、
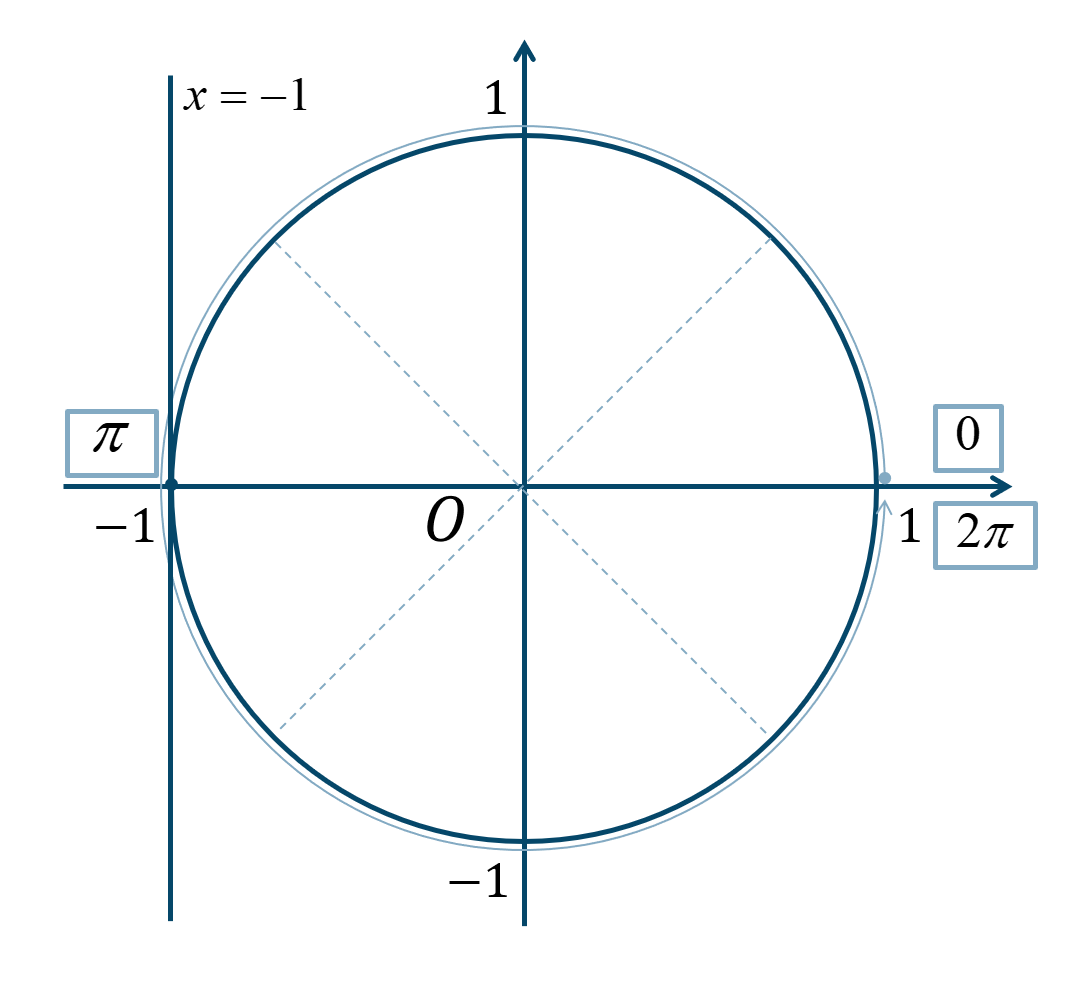
\(0≦\theta<2\pi\) の範囲で考えると、答えは$$~~~\theta=\pi$$となります。
[ 解答を見る ]
次の単位円より、
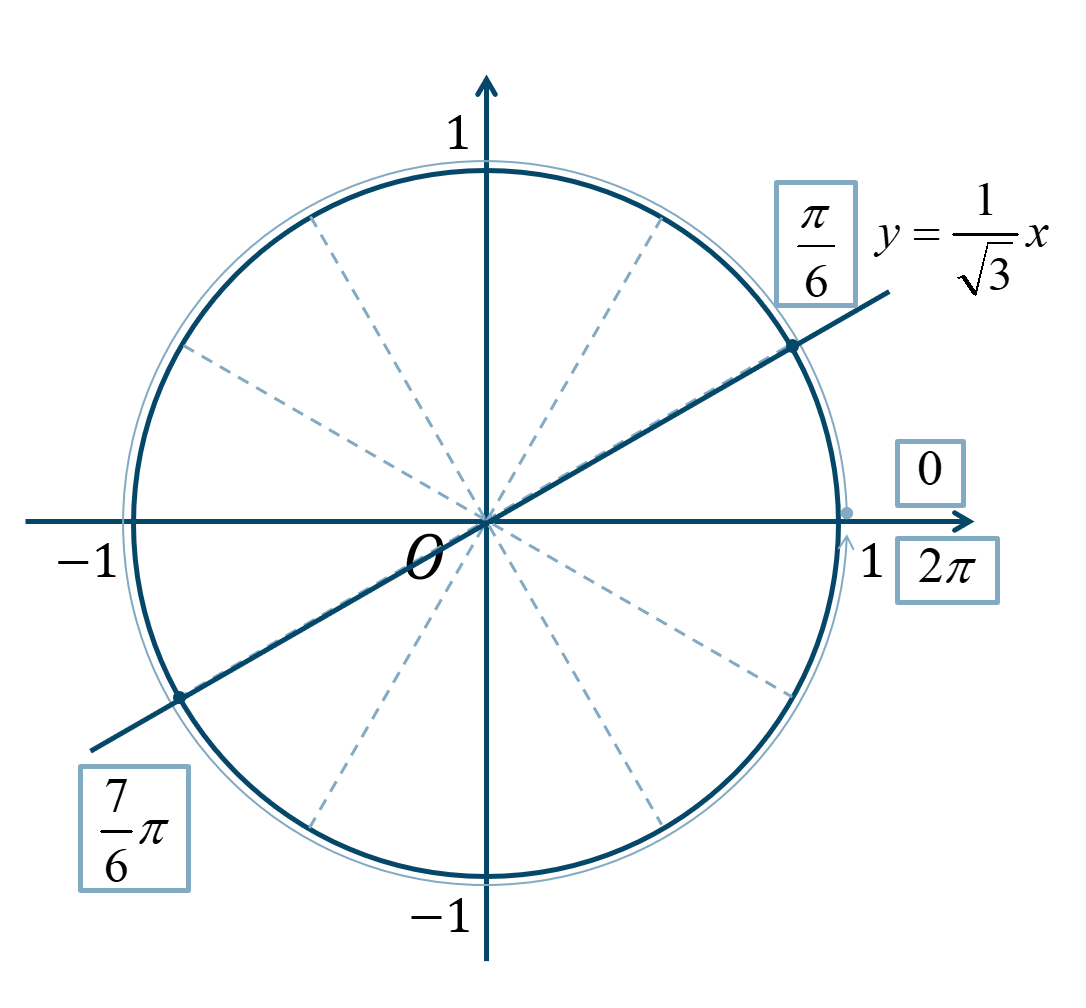
\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{6}}\) が1個分と7個分となります。
よって、答えは$$~~~\theta=\frac{\pi}{6}~,~\frac{7}{6}\pi$$となります。
[ 解答を見る ]
次の単位円より、

\(0≦\theta<2\pi\) の範囲で考えると、答えは$$~~~\theta=0~,~\pi$$となります。
[ 解答を見る ]
次の単位円より、
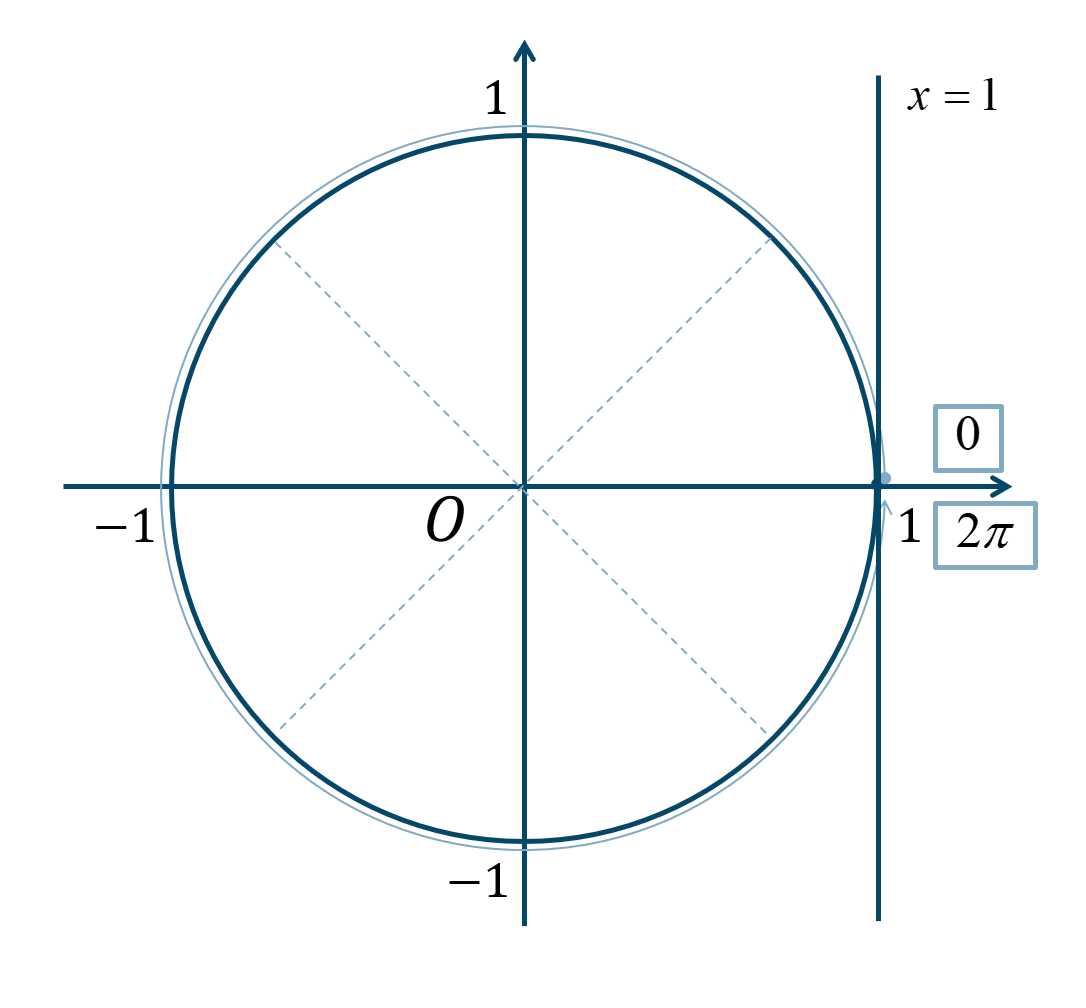
\(0≦\theta<2\pi\) の範囲で考えると、答えは$$~~~\theta=0$$となります。
[ 解答を見る ]
次の単位円より、
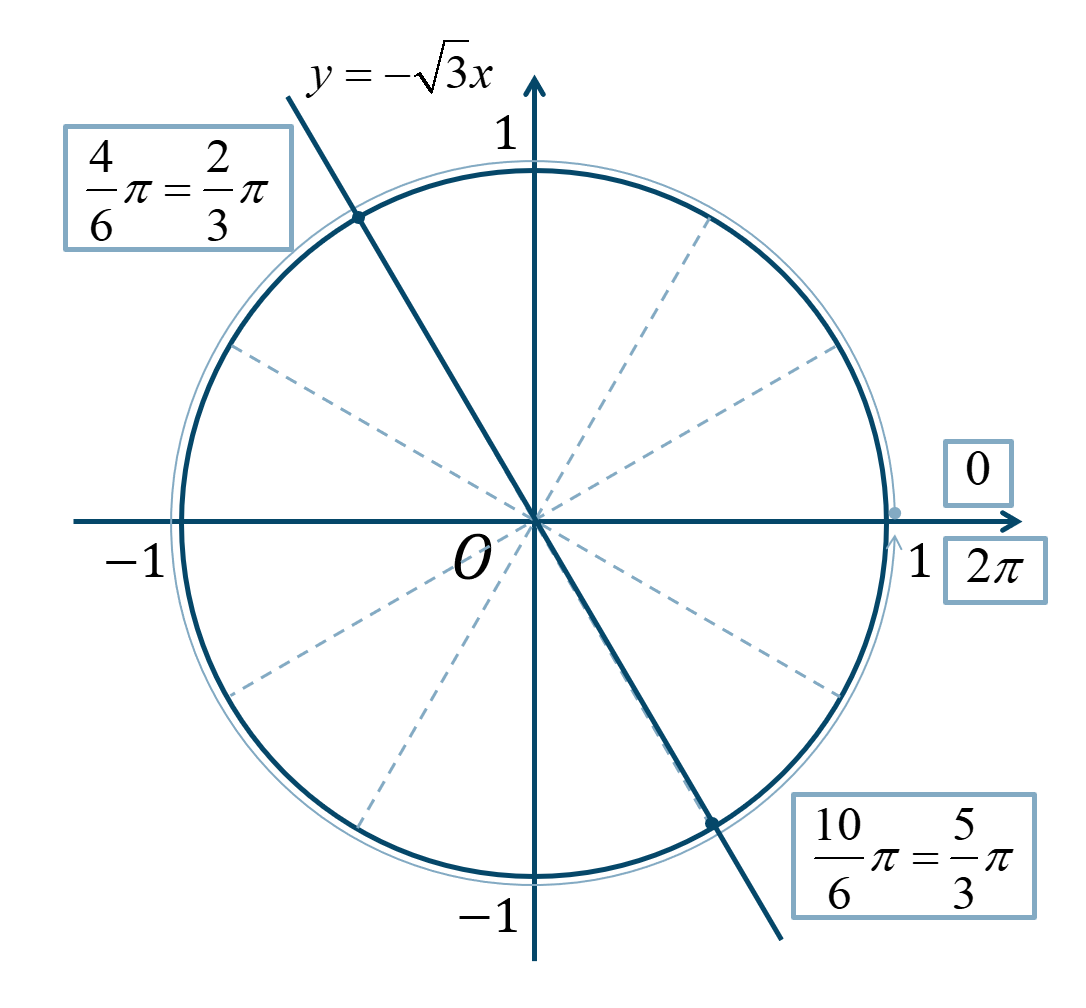
\(0≦\theta<2\pi\) の範囲で、\({\Large \frac{\pi}{6}}\) が4個分と10個分となります。
よって、答えは$$~~~\theta=\frac{2}{3}\pi~,~\frac{5}{3}\pi$$となります。



