三角関数を含む不等式
\(x\) 座標が \(a\) 以上になればよいので、単位円上に直線 \(x=a\) を引きその直線より右側の範囲になります。
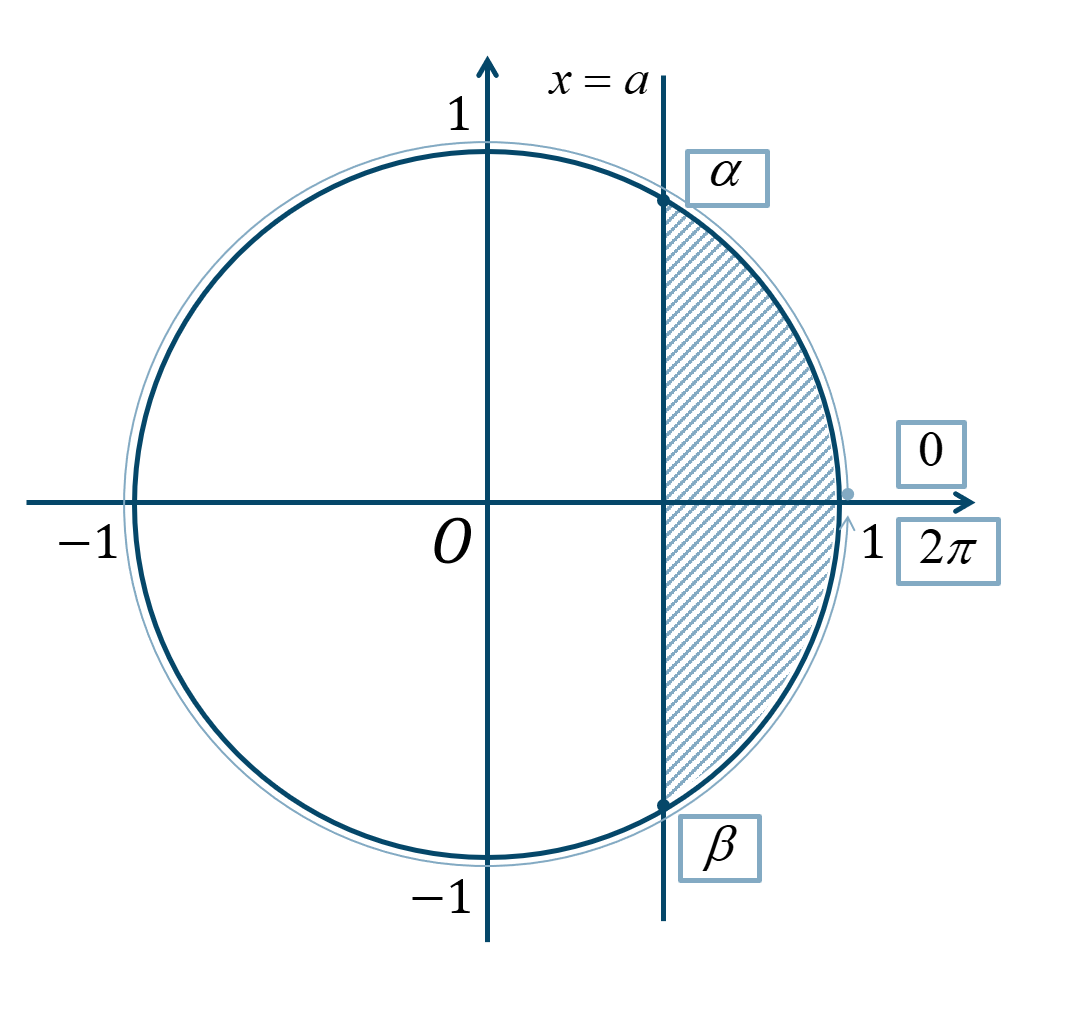
よって、\(0≦\theta<2\pi\) の範囲で解を求めると、$$~~~0≦\theta≦\alpha~,~\beta≦\theta<0$$となります。 ② \(\sin{\theta}>b\) のとき
\(y\) 座標が \(b\) より大きくなればよいので、単位円上に直線 \(y=b\) を引きその直線より上側の範囲になります。
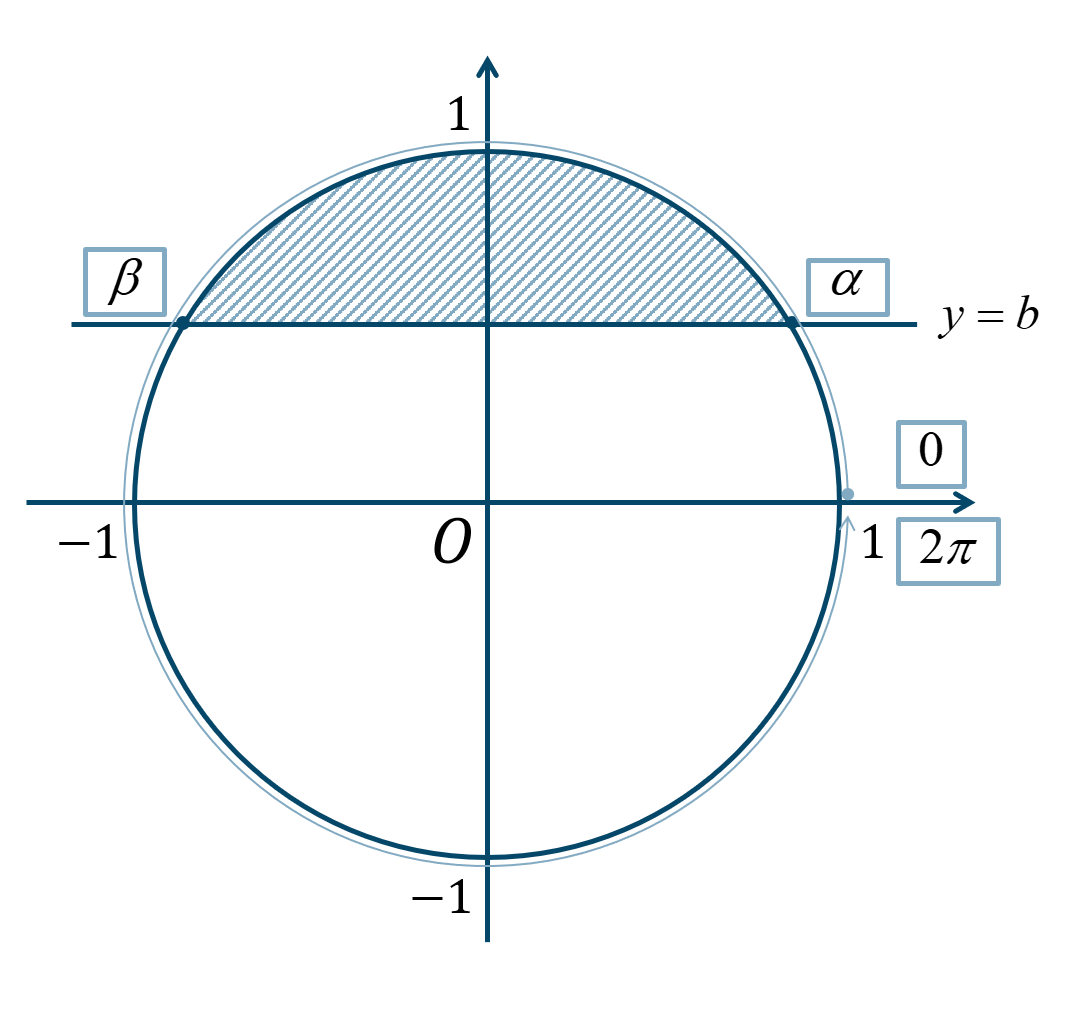
よって、\(0≦\theta<2\pi\) の範囲で解を求めると、$$~~~\alpha<\theta<\beta$$となります。 ③ \(\tan{\theta}≧m\)
傾きが \(m\) 以上となればよいので、単位円上に直線 \(y=mx\) を引きます。ただし、\(m>0\) とします。
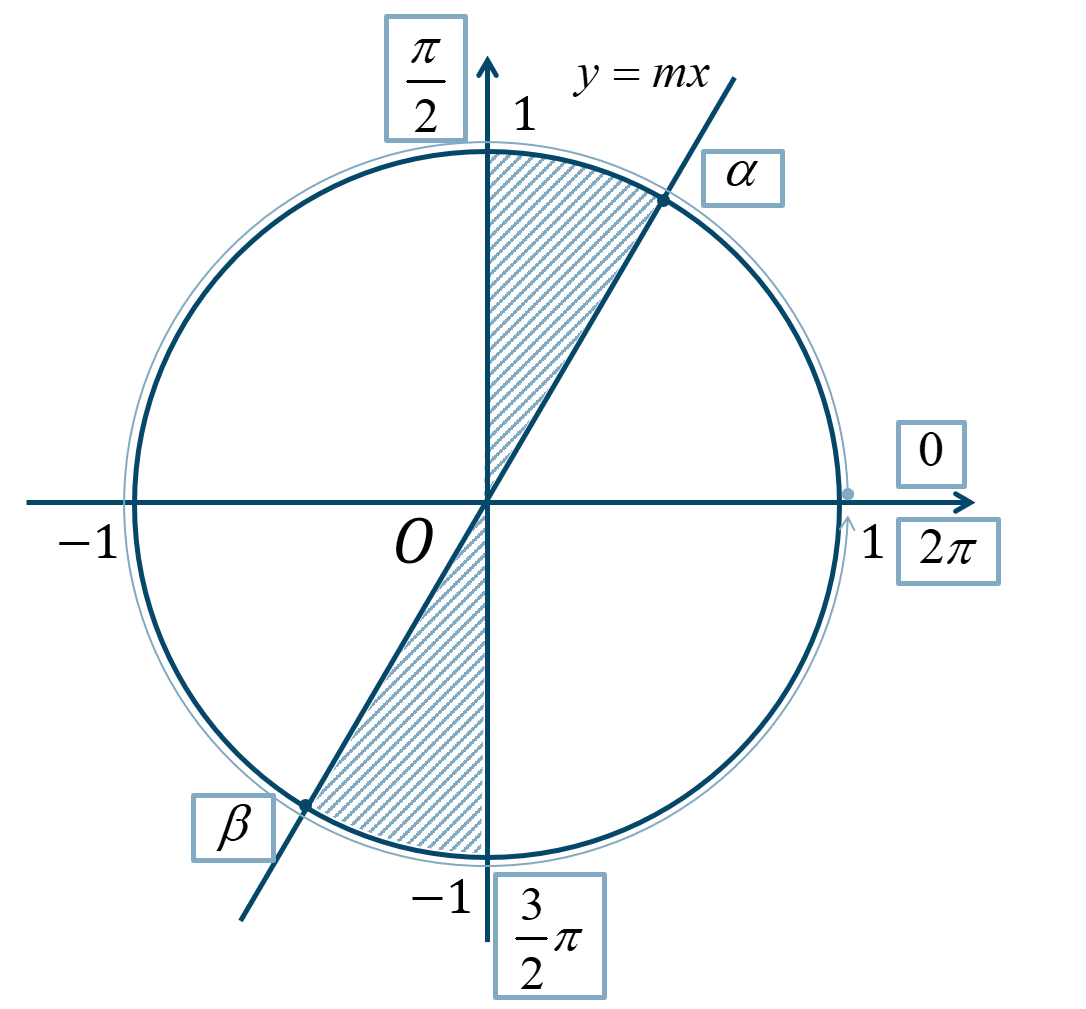
この図の斜線部分であれば、傾きが \(m\) 以上となるので、\(0≦\theta<2\pi\) の範囲で解を求めると、$$~~~\alpha≦\theta<\frac{\pi}{2}~,~\beta≦\theta<\frac{3}{2}\pi$$となります。 このとき、\(\theta={\Large \frac{\pi}{2}}~,~{\Large \frac{3}{2}}\pi\) は \(\tan{\theta}\) の値が定まらないので含みません。 また、\(\tan{\theta}≦m\) のときでは、
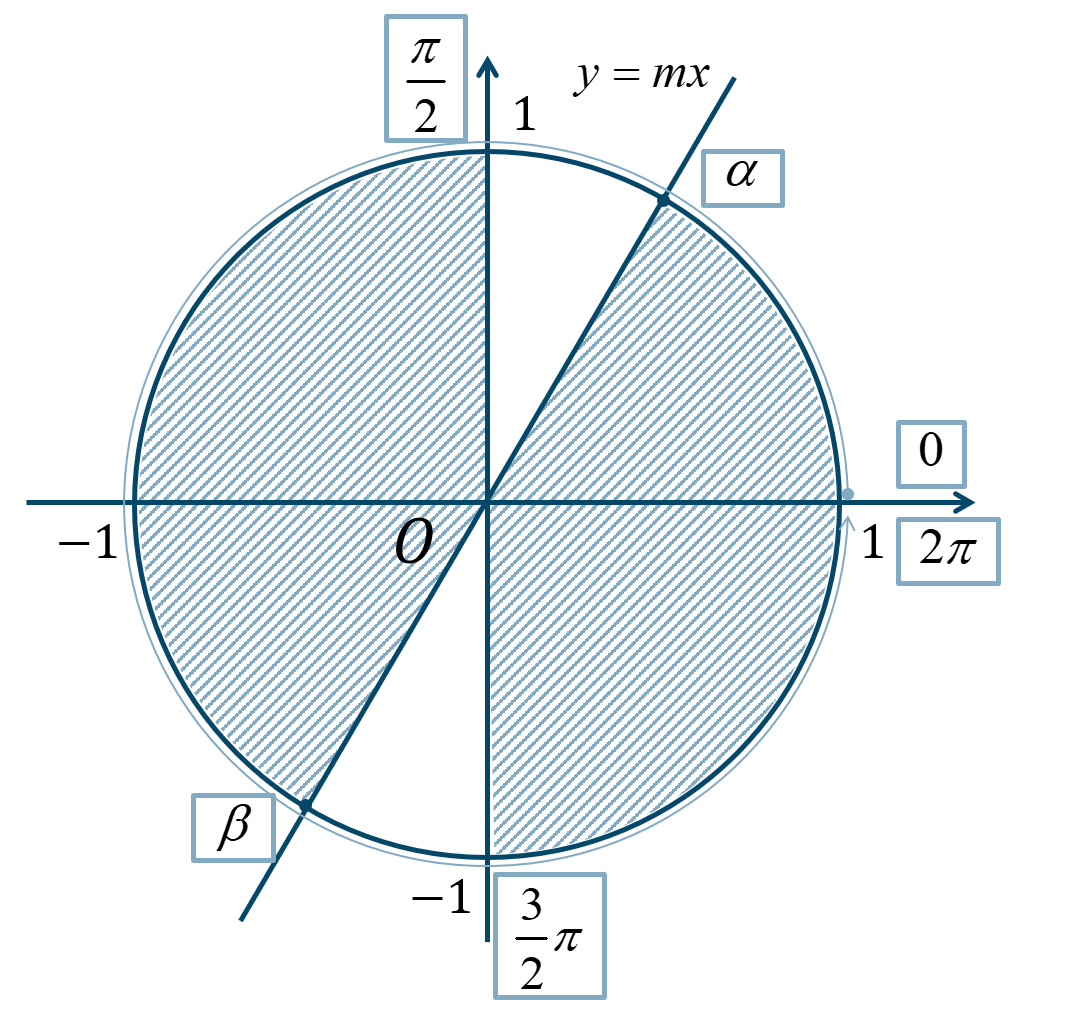
傾きが \(m\) より小さくなればよいので、上の斜線部分となります。このとき、第2象限と第4象限は傾きが負となる範囲で解に含まれます。よって、\(0≦\theta<2\pi\) の範囲で解を求めると、$$~~~0≦\theta≦\alpha~,~\frac{\pi}{2}<\theta≦\beta~,~\frac{3}{2}\pi<\theta<2\pi$$となります。
問題:三角関数を含む不等式①
問題解説(1)
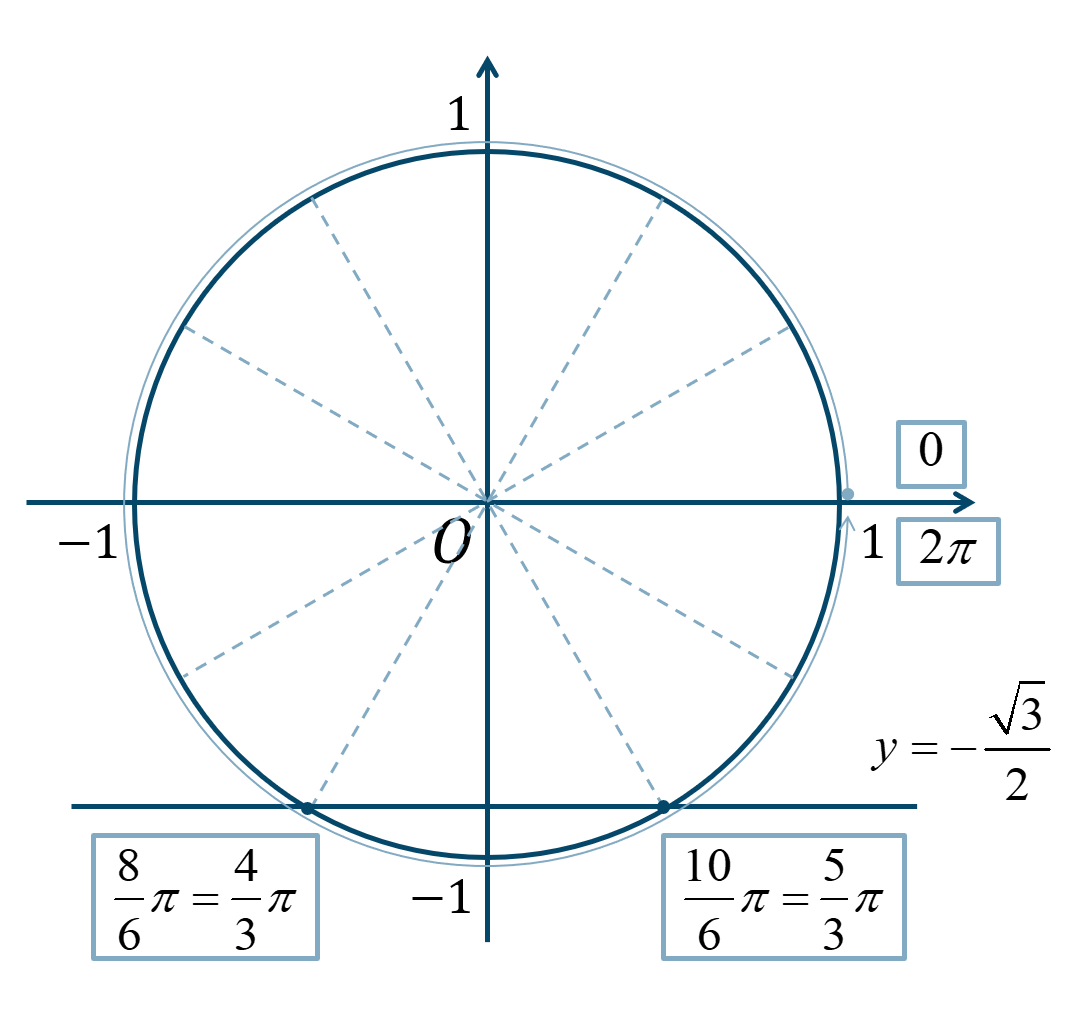
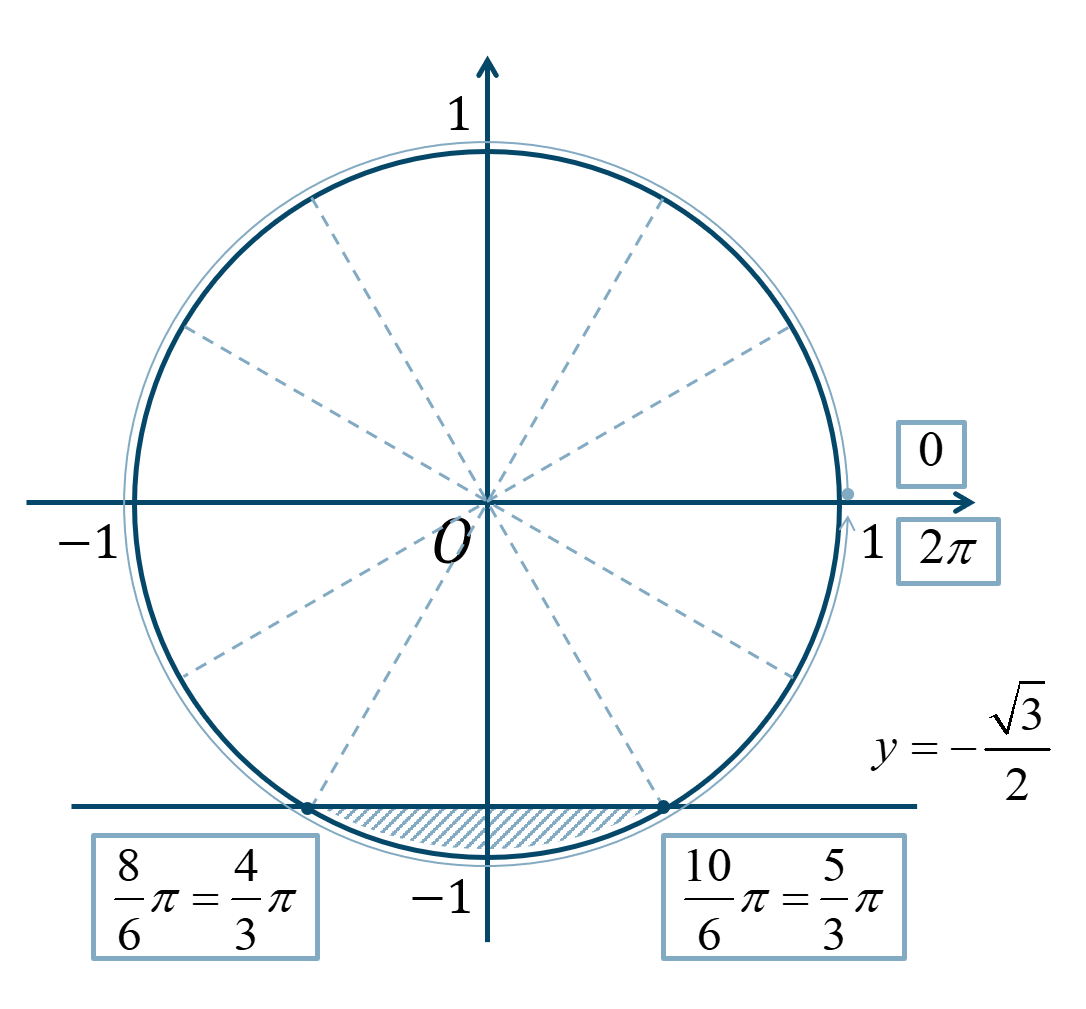
直線 \(y=-{\Large \frac{\sqrt{3}}{2}}\) と単位円との交点は、
\({\Large \frac{\pi}{6}}\) が8個分と10個分となるので、$$~~~\frac{8}{6}\pi=\frac{4}{3}\pi~,~\frac{10}{6}\pi=\frac{5}{3}\pi$$したがって、単位円上で直線 \(y=-{\Large \frac{\sqrt{3}}{2}}\) より下側の範囲となるので、
\(0≦\theta<2\pi\) の範囲で解を求めると答えは、$$~~~\frac{4}{3}\pi≦\theta≦\frac{5}{3}\pi$$となります。
問題解説(2)
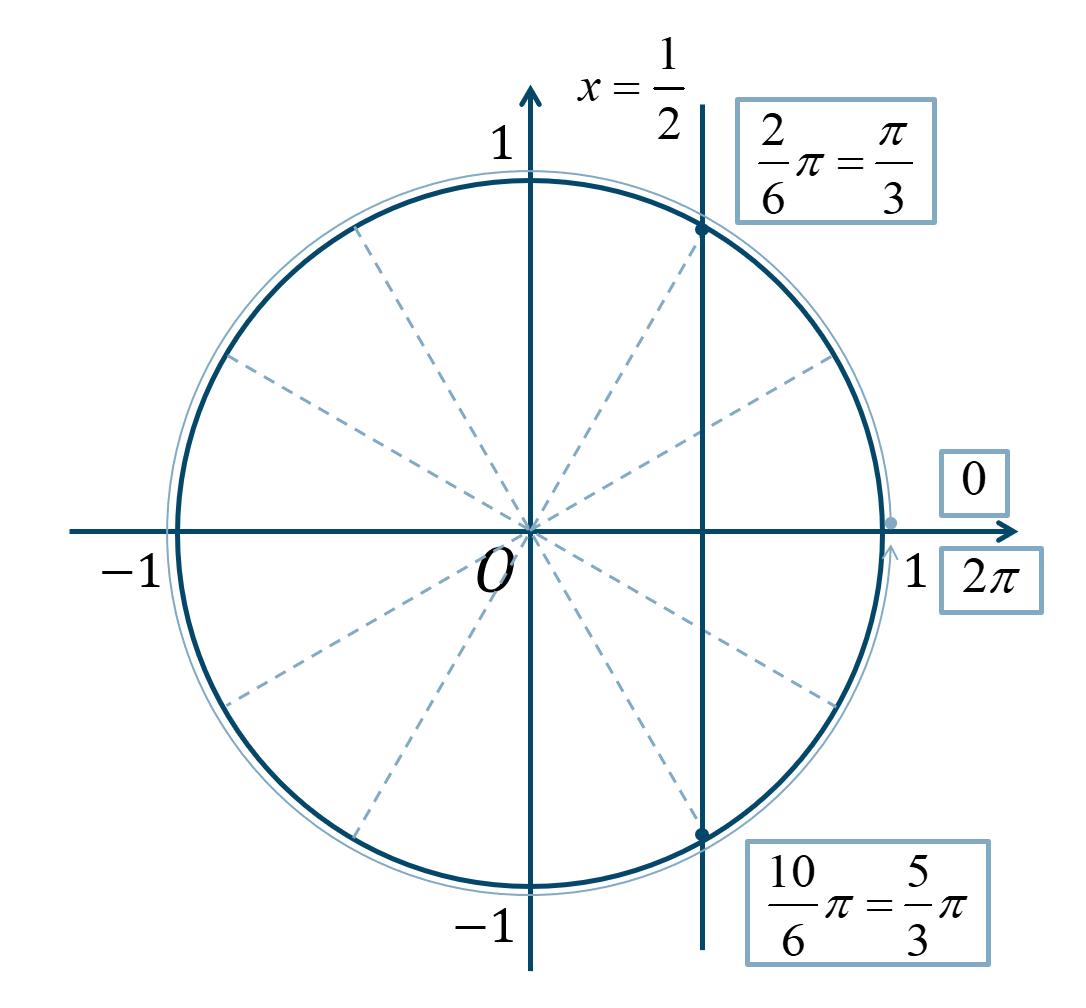
直線 \(x={\Large \frac{1}{2}}\) と単位円との交点は、
\({\Large \frac{\pi}{6}}\) が2個分と10個分となるので、$$~~~\frac{2}{6}\pi=\frac{\pi}{3}~,~\frac{10}{6}\pi=\frac{5}{3}\pi$$したがって、単位円上で直線 \(x={\Large \frac{1}{2}}\) より右の範囲となるので、
\(0≦\theta<2\pi\) の範囲で解を求めると答えは、$$~~~0≦\theta<\frac{\pi}{3}~,~\frac{5}{3}\pi<\theta<2\pi$$となります。
問題解説(3)
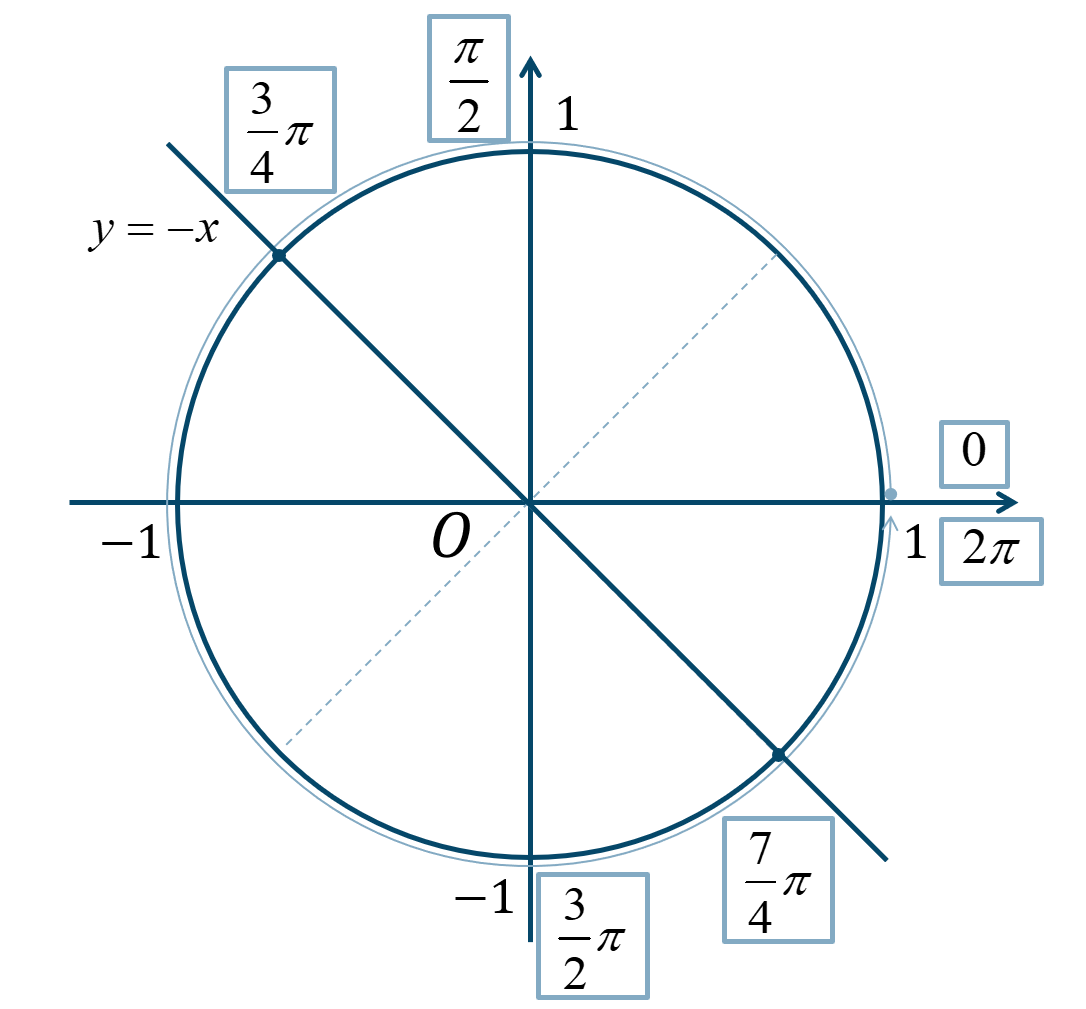
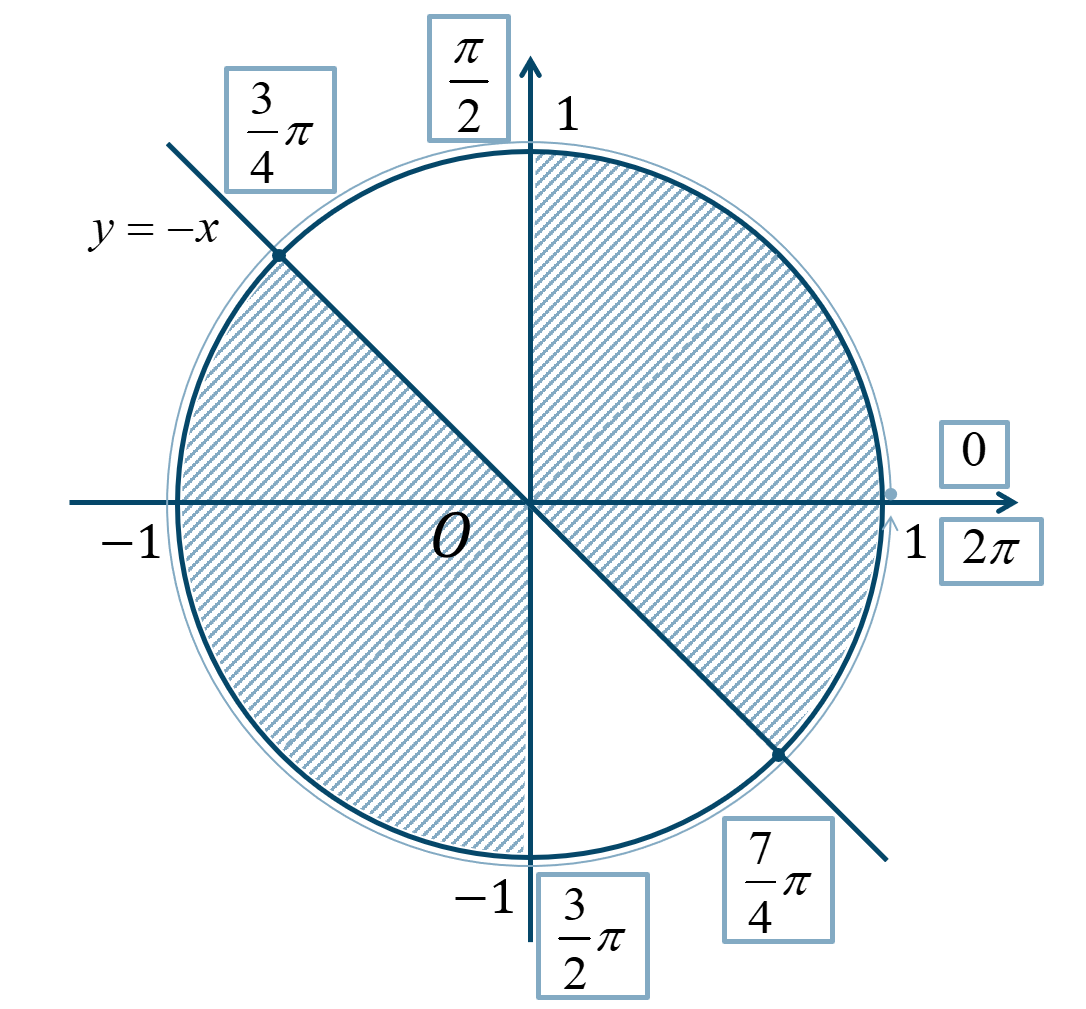
直線 \(y=-x\) と単位円との交点は、
\({\Large \frac{\pi}{4}}\) が3個分と7個分となるので、$$~~~\frac{3}{4}\pi~,~\frac{7}{4}\pi$$したがって、単位円上で直線 \(y=-x\) より傾きが大きい範囲となり、第1象限と第3象限も含むので、
\(0≦\theta<2\pi\) の範囲で解を求めると答えは、$$~~~0≦\theta<\frac{\pi}{2}~,~\frac{3}{4}\pi≦\theta<\frac{3}{2}\pi$$$$~~~\frac{7}{4}\pi≦\theta<2\pi$$となります。
今回のまとめ
三角関数を含む不等式の角は、単位円の内部とその不等式の領域の共通範囲より、解の範囲を求めましょう。