三角関数を含む2次不等式
② 1種類にした \(\sin{\theta}(\cos{\theta})\) を別の文字 \(t\) に置き換えます。このとき、\(t\) の値の範囲に注意しましょう。
③ 置き換えた \(t\) の2次不等式として解を求めます。
④ \(t\) を三角関数の式に戻して、\(\theta\) の値の範囲を求めます。
問題解説:三角関数を含む2次不等式
1次式の三角関数が \(\sin{\theta}\) であることより、\(\sin{\theta}\) で統一しましょう。
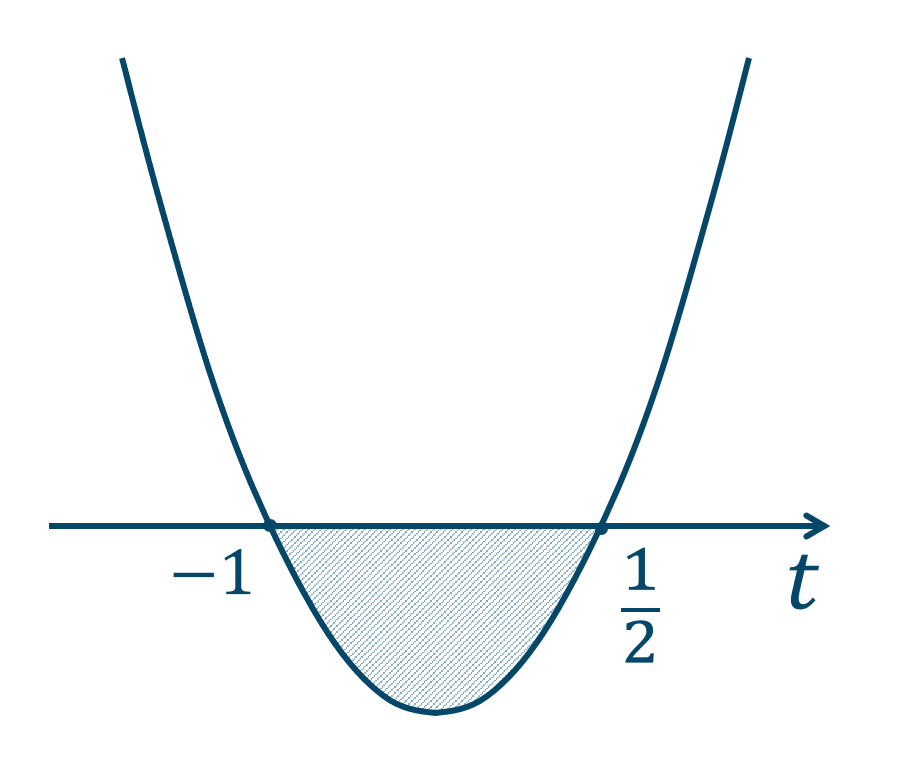
\(\cos^2{\theta}=1-\sin^2{\theta}\) より、$$\hspace{ 10 pt} 2(1-\sin^2{\theta})-\sin{\theta}-1≧0$$$$\hspace{ 15 pt} 2-2\sin^2{\theta}-\sin{\theta}-1≧0$$$$\hspace{ 24 pt}-2\sin^2{\theta}-\sin{\theta}+1≧0$$両辺に \(-1\) をかけると、不等号の向きが逆になるので、$$\hspace{ 10 pt}2\sin^2{\theta}+\sin{\theta}-1≦0$$ここで、\(\sin{\theta}=t\) とすると、値の範囲は \(0≦\theta<2\pi\) より、$$~~~-1≦t≦1$$式を置き換えると、$$\hspace{ 10 pt}2t^2+t-1≦0$$左辺を因数分解すると、$$\hspace{ 10 pt}(2t-1)(t+1)≦0$$
グラフより、$$\hspace{ 10 pt}-1≦t≦\frac{1}{2}$$\(t=\sin{\theta}\) と元に戻すと、$$\hspace{ 10 pt}-1≦\sin{\theta}≦\frac{1}{2}$$
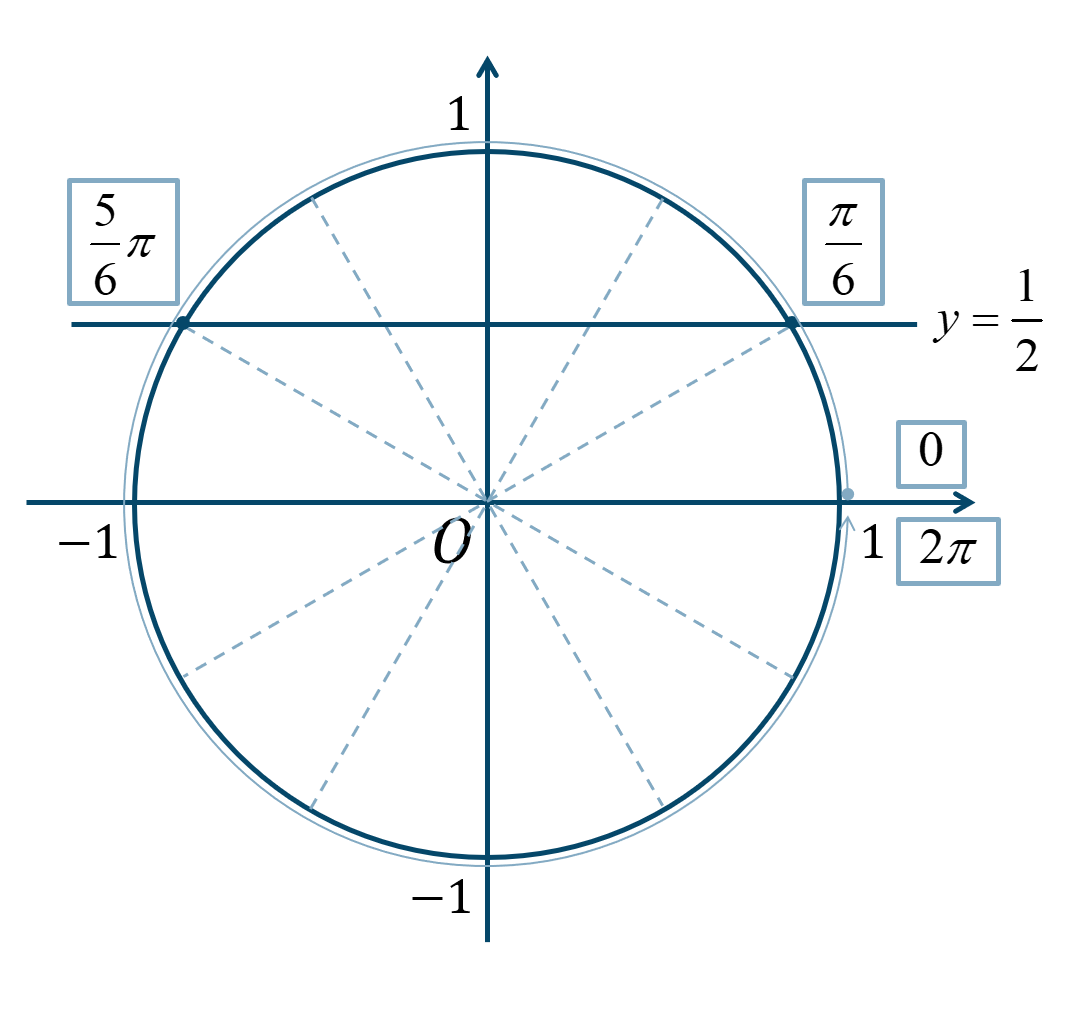
ここで、\(y={\Large \frac{1}{2}}\) と単位円との交点より、
\({\Large \frac{\pi}{6}}\) が1個分と5個分となるので、$$~~~\theta=\frac{\pi}{6}~,~\frac{5}{6}\pi$$
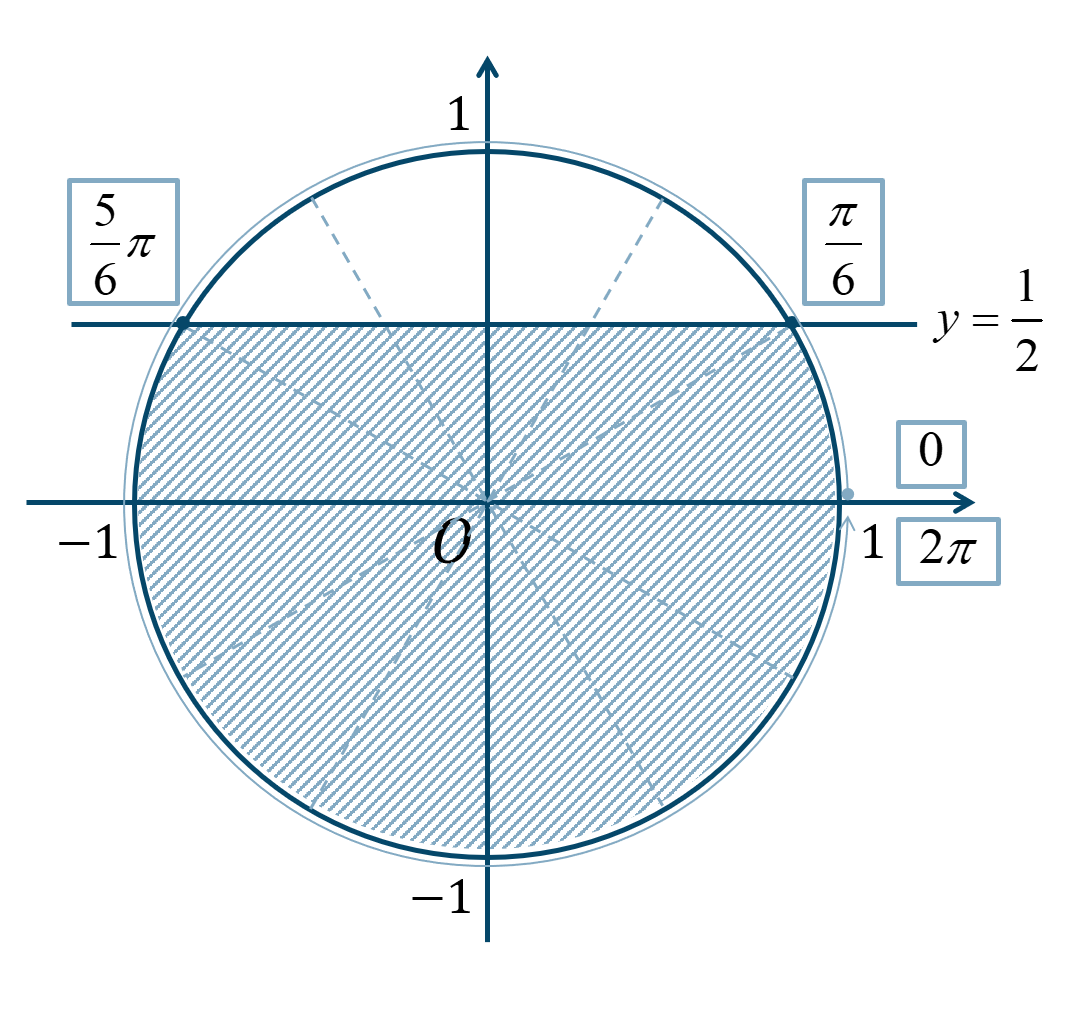
よって、単位円上で以下の範囲を \(0≦\theta<2\pi\) で考えると、$$~~~ -1≦\sin{\theta}≦\frac{1}{2}$$
よって、答えは$$~~~0≦\theta≦\frac{\pi}{6}~,~\frac{5}{6}\pi≦\theta<2\pi$$となります。
今回のまとめ
三角関数を含む2次不等式は置き換えをし、まずは2次不等式を解きます。三角関数に戻して、単位円より解の範囲を求めましょう。