2直線のなす角
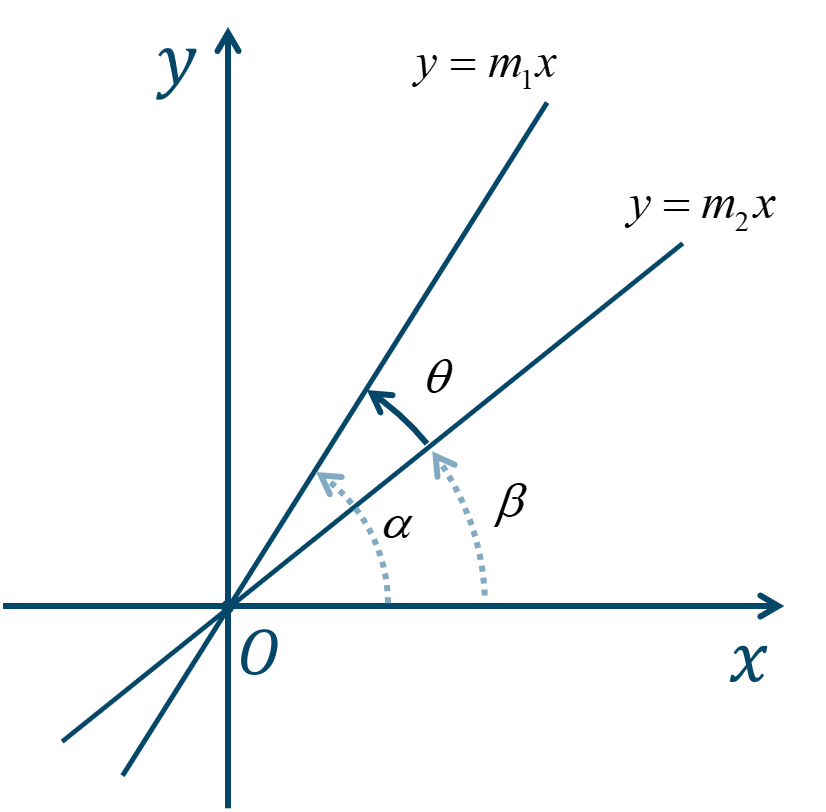
② それぞれ \(x\) 軸の正の部分となす角を \(\alpha~,~\beta\) とすると、$$~~~\tan{\alpha}=m_1~,~\tan{\beta}=m_2$$となります。
③ ここで2直線のなす角 \(\theta\) は、$$~~~\theta=\alpha-\beta$$となり、\(\theta\) は鋭角で答えるので \(\tan{\theta}\) の値をは正の数となるので、$$~~~\tan{\theta}=|\tan{(\alpha-\beta)}|$$となります。
④ 加法定理より、$$~~~|\tan{(\alpha-\beta)}|=\left| \frac{\tan{\alpha}-\tan{\beta}}{1+\tan{\alpha}\tan{\beta}} \right|$$これに、②で求めた値を代入して \(\theta\) の値を求めます。
問題解説:2直線のなす角
この2直線のなす角を \(\theta\) とすると、2直線を原点を通る直線に平行移動したときのなす角に等しくなります。
\(y=+{\Large \frac{\sqrt{3}}{5}}x\) と \(x\) 軸の正の部分となす角を \(\alpha\) とすると、$$~~~\tan{\alpha}=-\frac{\sqrt{3}}{5}~\cdots{\large ①}$$
\(y={\Large \frac{\sqrt{3}}{2}}x\) と \(x\) 軸の正の部分となす角を \(\beta\) とすると、$$~~~\tan{\beta}=\frac{\sqrt{3}}{2}~\cdots{\large ②}$$
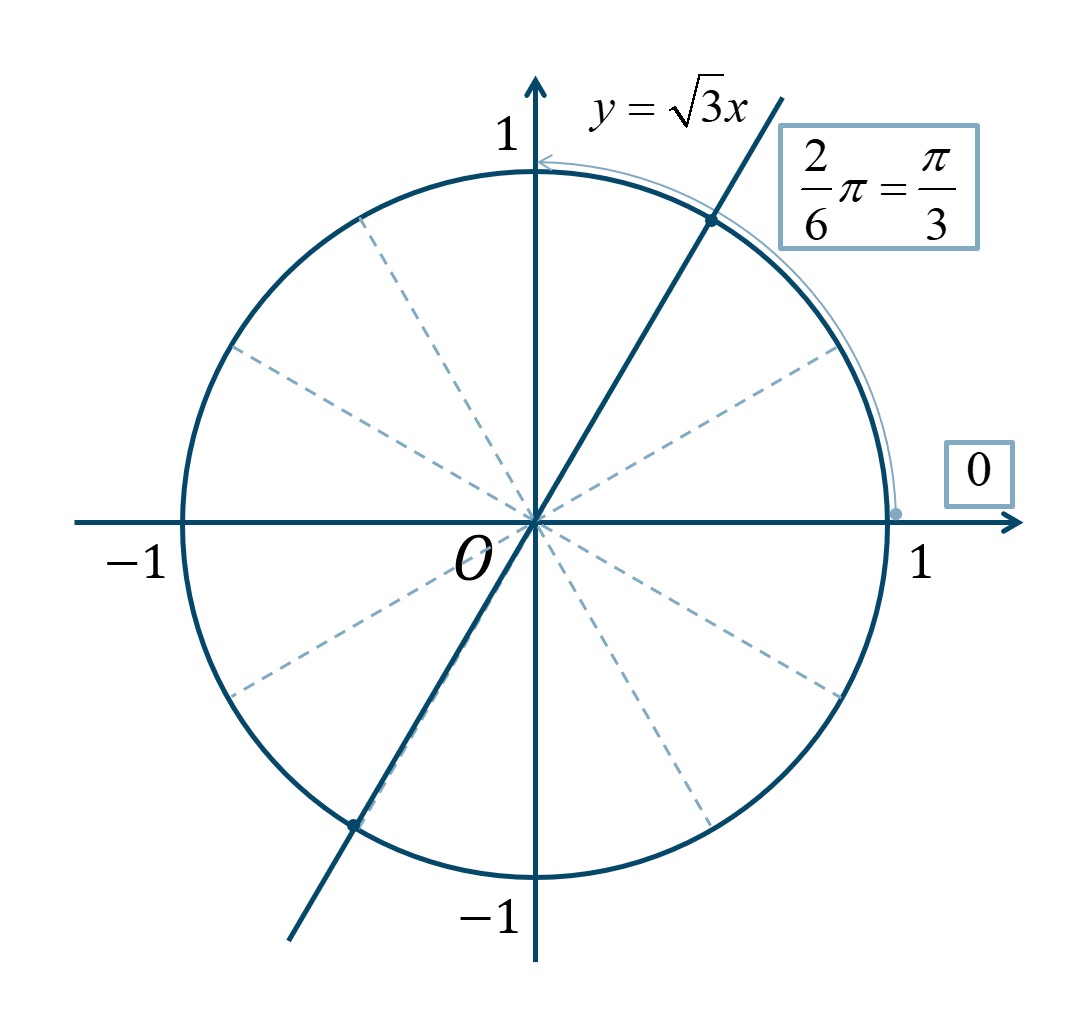
ここで、\(\theta\) は鋭角で、$$~~~\theta=\alpha-\beta$$よって、$$~~~\tan{\theta}=|\tan{(\alpha-\beta)}|$$加法定理より、$$~~~~~~|\tan{(\alpha-\beta)}|$$$$~=\left| \frac{\tan{\alpha}-\tan{\beta}}{1+\tan{\alpha}\tan{\beta}} \right|$$①と②を代入すると、$$~=\left| \frac{-{\large \frac{\sqrt{3}}{5}}-{\large \frac{\sqrt{3}}{2}}}{1+\left(-{\large \frac{\sqrt{3}}{5}}\right)\cdot {\large \frac{\sqrt{3}}{2}}} \right|$$$$~=\left| \frac{-{\large \frac{\sqrt{3}}{5}}-{\large \frac{\sqrt{3}}{2}}}{1-{\large \frac{3}{10}}} \right|$$分母分子に \(10\) をかけると、$$~=\left| \frac{\left(-{\large \frac{\sqrt{3}}{5}}-{\large \frac{\sqrt{3}}{2}}\right)\cdot 10}{\left(1-{\large \frac{3}{10}}\right)\cdot 10} \right|$$$$~=\left| \frac{-2\sqrt{3}-5\sqrt{3}}{10-3} \right|$$$$~=\left| \frac{-7\sqrt{3}}{7} \right|$$$$~=|-\sqrt{3}|$$$$~=\sqrt{3}$$よって、単位円と直線 \(y=\sqrt{3}x\) との交点より、
\(\theta\) は鋭角であるので、答えは$$~~~\theta=\frac{\pi}{3}$$となります。
今回のまとめ
2直線のなす角の問題は傾きと \(\tan{}\) の関係と、正接の加法定理を用いて計算しましょう。また、鋭角で答えるときは絶対値を付けておきましょう。