２倍角を含む方程式・不等式の解法
① ２倍角の公式を代入します。$$~~~\sin{2x}=2\sin{x}\cos{x}$$② \(\sin{x}\)\(~,~\)\(\cos{x}\) だけの式を因数分解して方程式・不等式を解きます。
(2) \(\cos{2x}\) を含む式
① ２倍角の公式を代入します。
( ⅰ ) \(\sin{x}\) がある場合$$~~~\cos{2x}=1-2\sin^2{x}$$( ⅱ ) \(\cos{x}\) がある場合$$~~~\cos{2x}=2\cos^2{x}-1$$② １種類の三角関数の２次式となるので、項を左辺にまとめ因数分解して方程式・不等式を解きます。
問題解説：２倍角を含む方程式・不等式
問題解説(1)
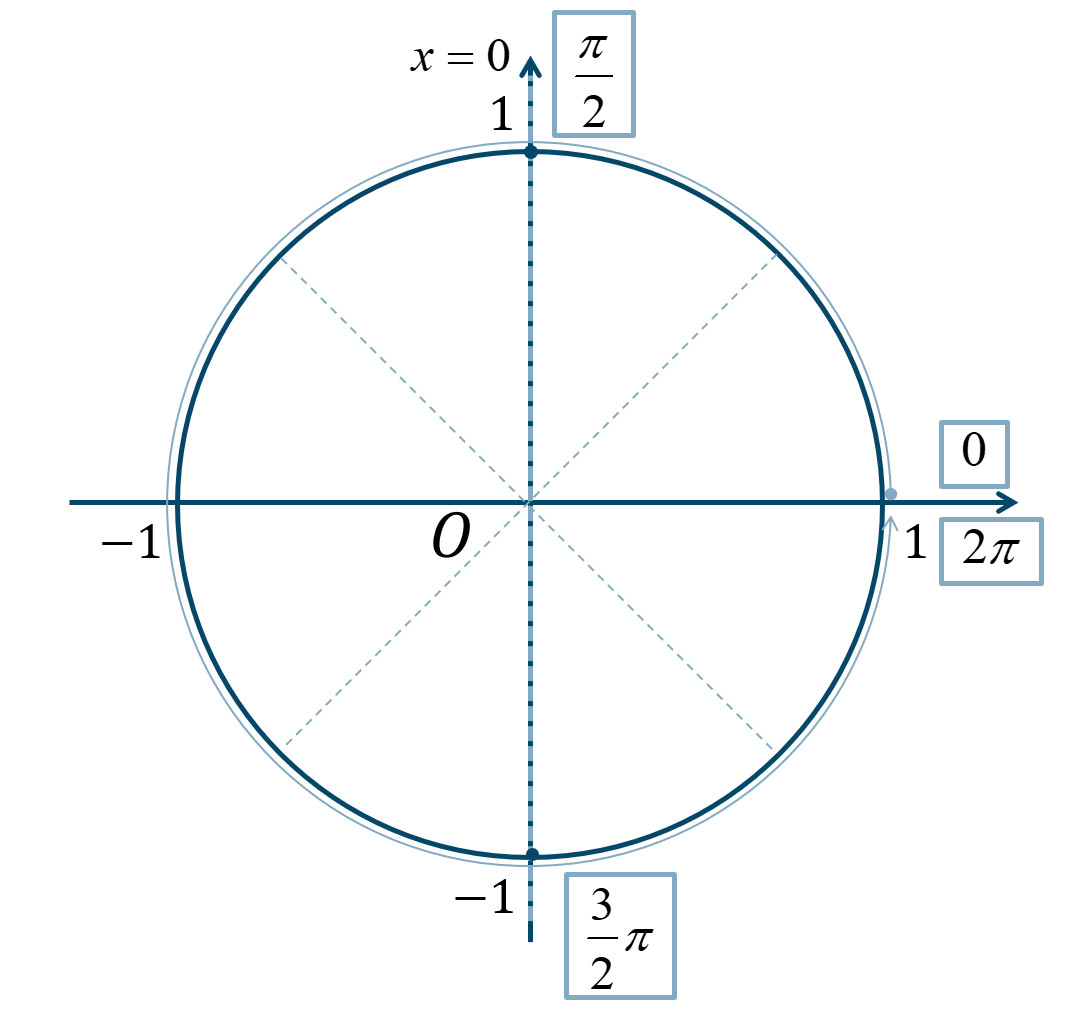
２倍角の公式より、$$\hspace{ 35 pt}\sin{2x}-\cos{x}=0$$$$\hspace{ 10 pt}2\sin{x}\cos{x}-\cos{x}=0$$共通因数でくくると、$$\hspace{ 10 pt}\cos{x}(2\sin{x}-1)=0$$これより、\(\cos{x}=0\) または \(2\sin{x}-1=0\) となるので、$$~~~\cos{x}=0$$このとき、単位円より \(0≦x<2\pi\) の範囲で解を求めると、
$$~~~x=\frac{\pi}{2}~,~\frac{3}{2}\pi$$また、$$\hspace{ 10 pt}2\sin{x}-1=0$$移項して \(2\) で割ると、$$\hspace{ 10 pt}2\sin{x}=1$$$$\hspace{ 16 pt}\sin{x}=\frac{1}{2}$$このとき、単位円より \(0≦x<2\pi\) の範囲で解を求めると、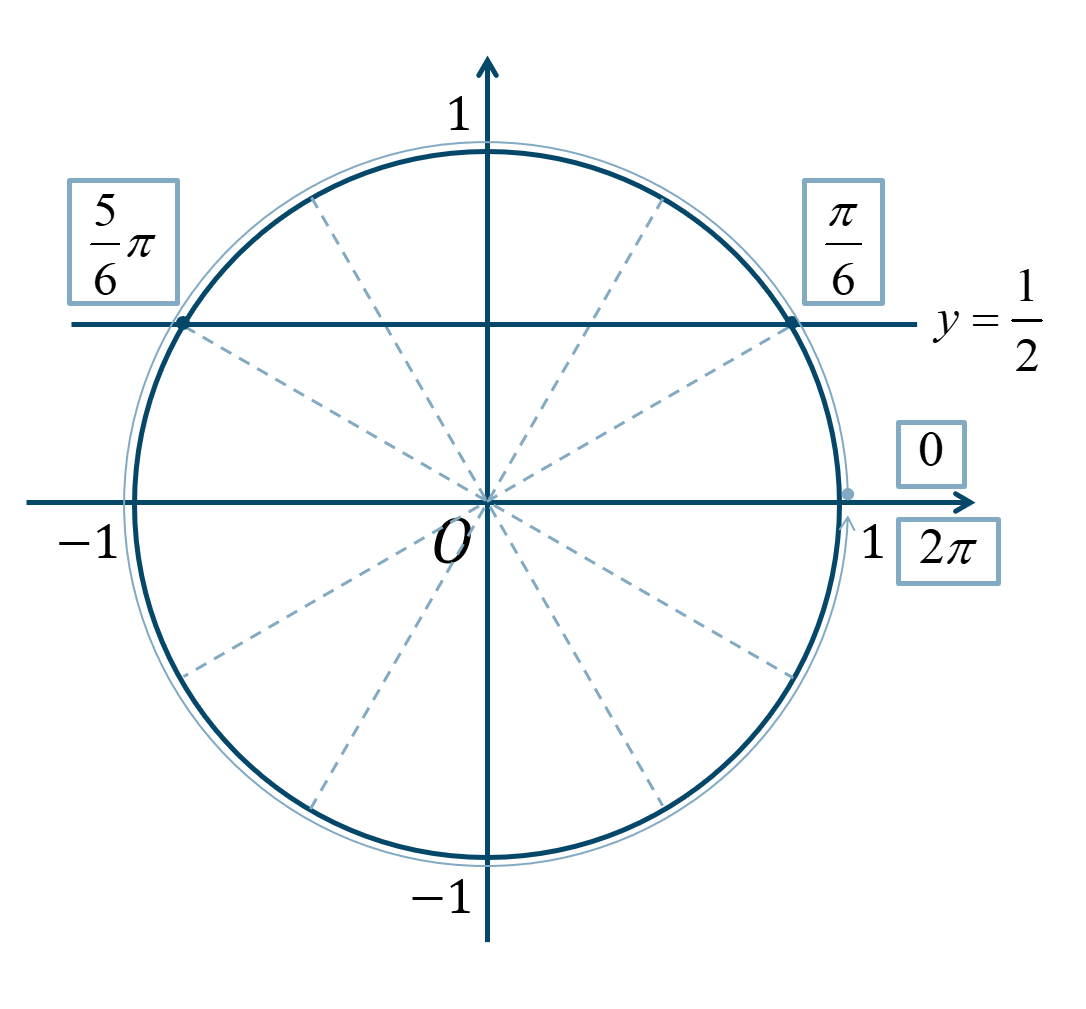
$$~~~x=\frac{\pi}{6}~,~\frac{5}{6}\pi$$以上より、求める答えは$$~~~x=\frac{\pi}{6}~,~\frac{\pi}{2}~,~\frac{5}{6}\pi~,~\frac{3}{2}\pi$$となります。
問題解説(2)
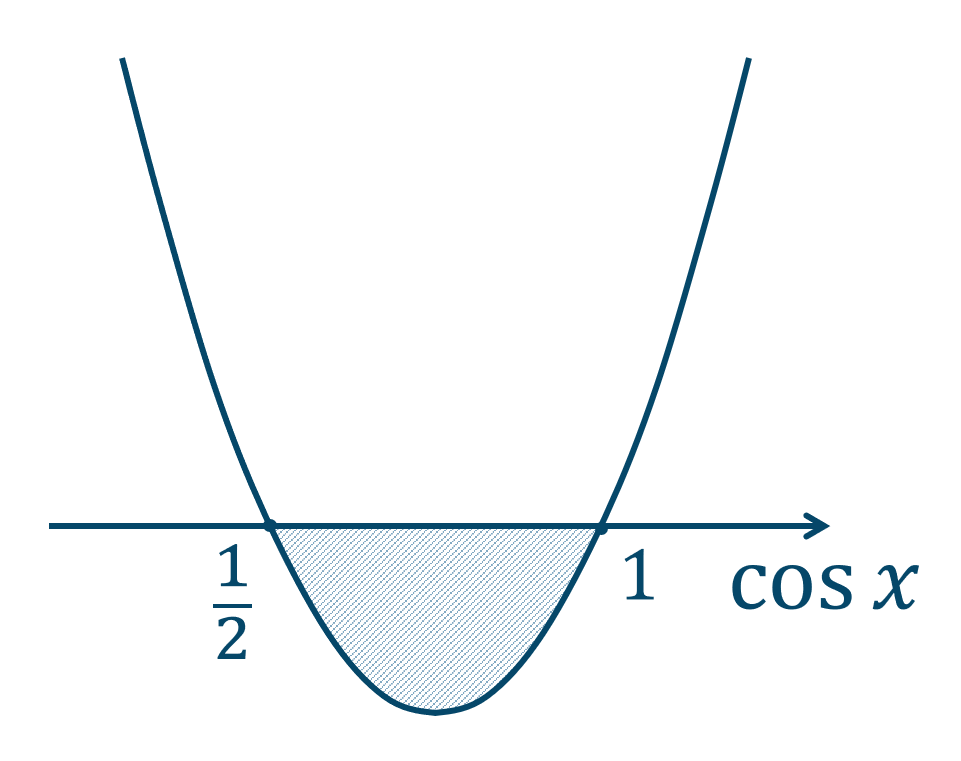
１次式に \(\cos{x}\) があるので、２倍角の公式 \(\cos{2x}=2\cos^2{x}-1\) を用いると、$$\hspace{ 10 pt}2\cos^2{x}-1-3\cos{x}+2≦0$$$$\hspace{ 27 pt}2\cos^2{x}-3\cos{x}+1≦0$$左辺を因数分解すると、$$\hspace{ 10 pt}(2\cos{x}-1)(\cos{x}-1)≦0$$ここで、２次不等式の解をグラフで考えると、$$~~~2\cos{x}-1=0~,~\cos{x}-1=0$$これらを解くと、$$~~~\cos{x}=\frac{1}{2}~,~1$$これらの解より、２次不等式のグラフは次のようになります。
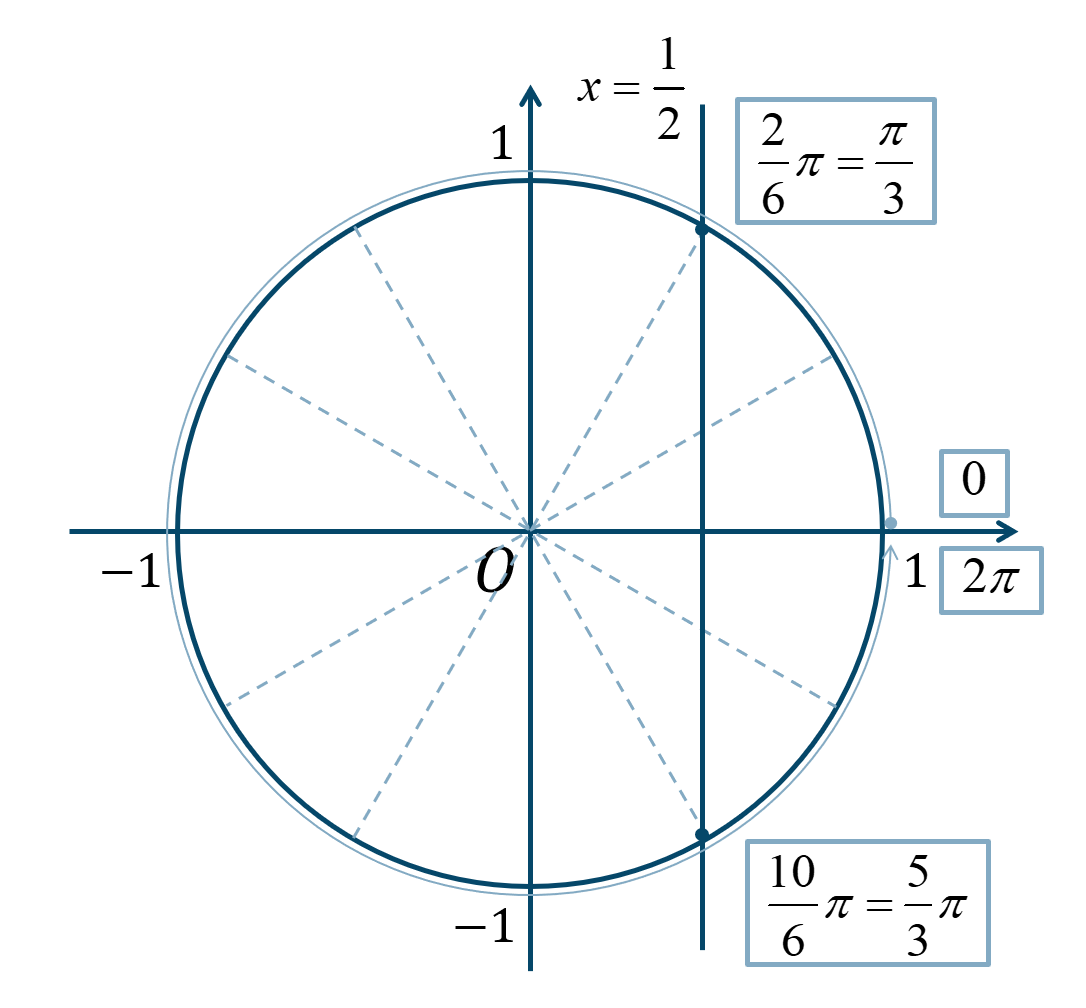
よって、$$~~~\frac{1}{2}≦\cos{x}≦1$$このとき、単位円より \(0≦x<2\pi\) の範囲で解を求めると、
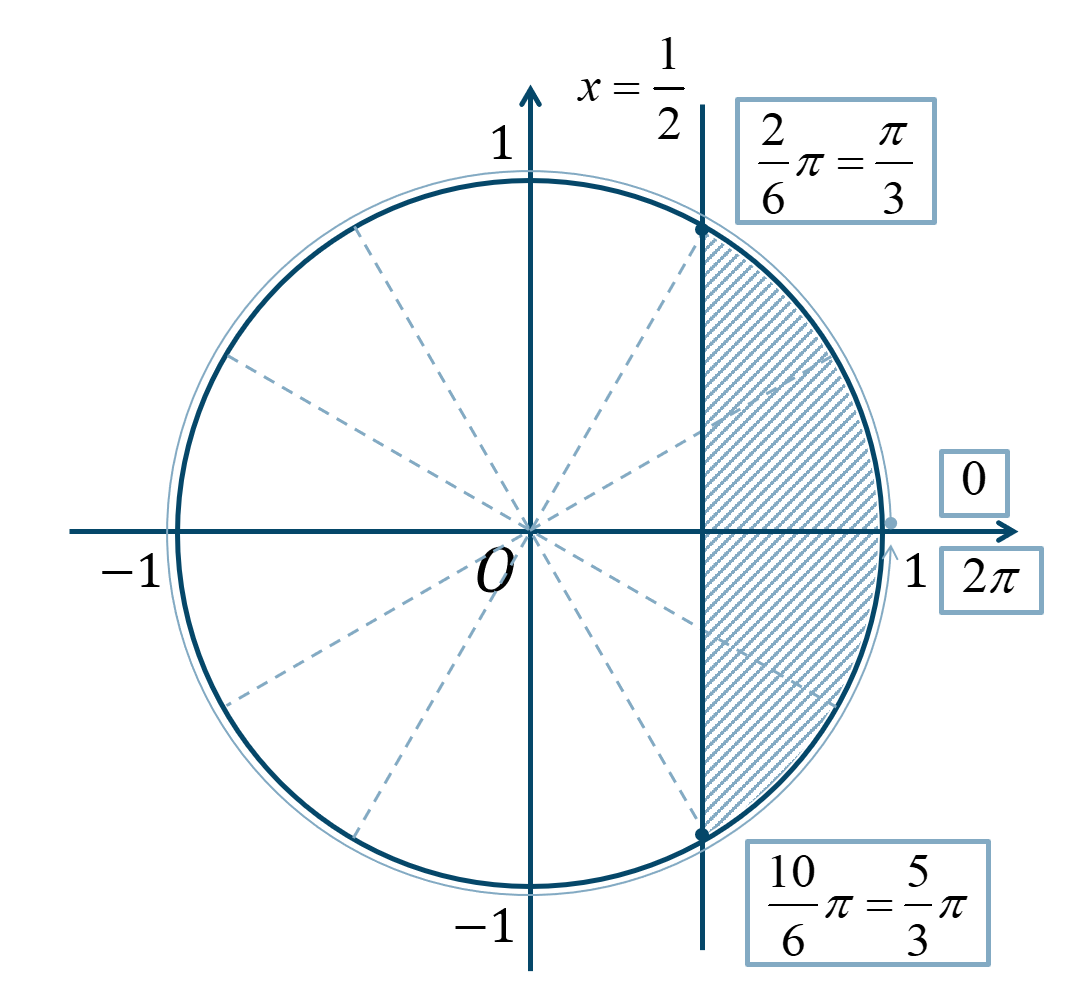
\({\Large \frac{\pi}{6}}\) が2個分と10個分の位置より右側の範囲となるので、$$~~~\frac{2}{6}\pi=\frac{\pi}{3}~,~\frac{10}{6}\pi=\frac{5}{3}\pi$$
よって、答えは、$$~~~0≦x≦\frac{\pi}{3}~,~\frac{5}{3}\pi≦x<2\pi$$となります。
今回のまとめ
２倍角を含む方程式・不等式は、１次式の三角関数に揃えるように公式を選択して計算していきましょう。
