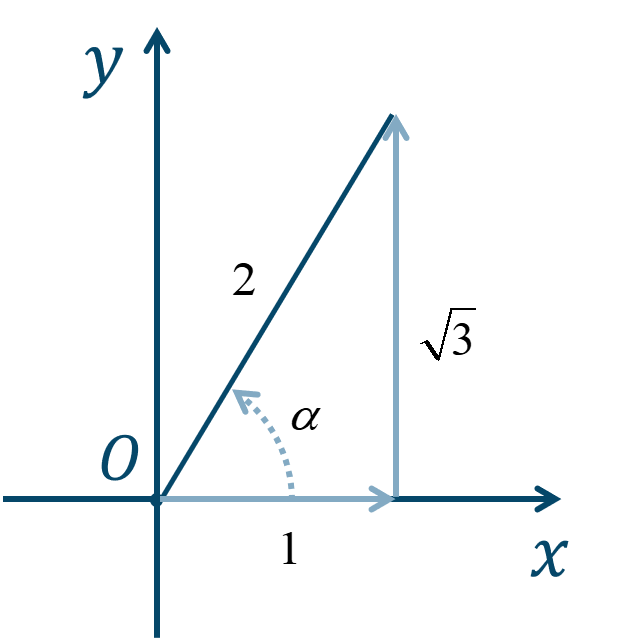三角関数の合成の解法
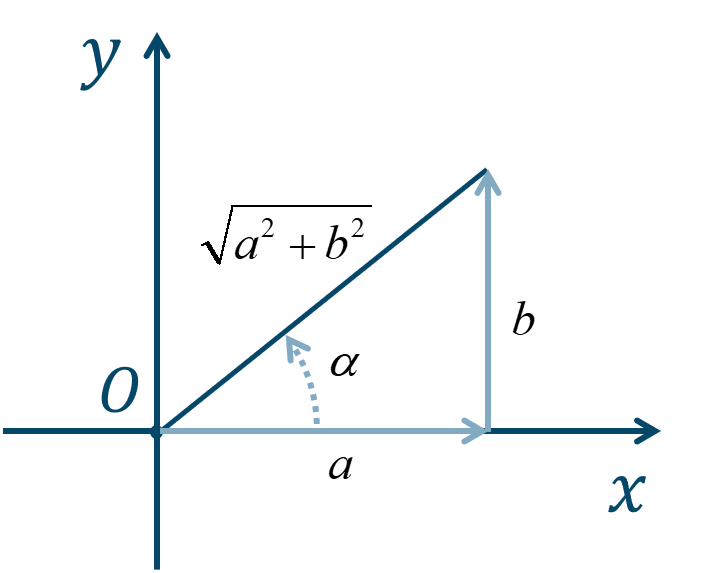
このとき、\(\alpha\) は次の図で表される角となります。\(\sin{}\) の係数値だけ右に進み、\(\cos{}\) の係数値だけ上に進むときの直線と \(x\) 軸の正の部分とのなす角を考えましょう。
この図より、
となります。
問題解説:三角関数の合成
問題解説(1)
$$~~~~~~\sqrt{1^2+(\sqrt{3})^2}$$$$~=\sqrt{1+3}$$$$~=\sqrt{4}$$$$~=2$$これと、次の図より、
$$~~~\alpha=\frac{\pi}{3}$$となります。
よって、合成の公式を用いると、答えは$$~~~\sin{\theta}+\sqrt{3}\cos{\theta}=2\sin{\left(\theta+\frac{\pi}{3}\right)}$$となります。
問題解説(2)
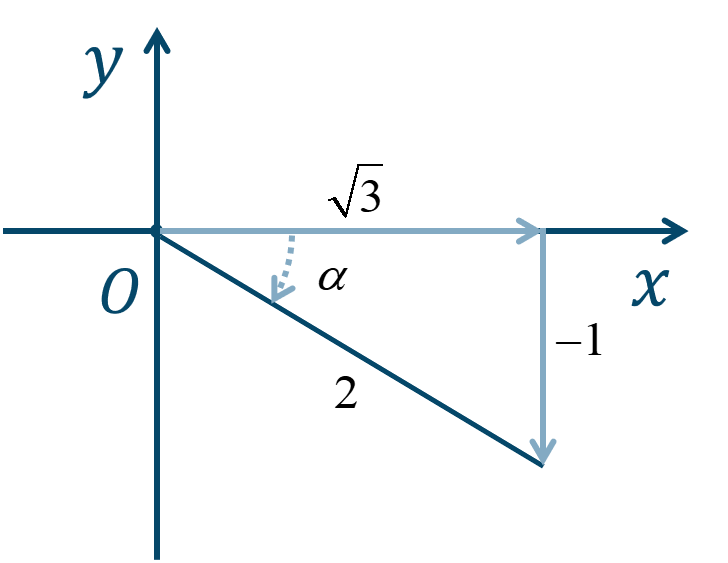
$$~~~~~~\sqrt{(\sqrt{3})^2+(-1)^2}$$$$~=\sqrt{3+1}$$$$~=\sqrt{4}$$$$~=2$$これと、次の図より、
$$~~~\alpha=-\frac{\pi}{6}$$となります。
よって、合成の公式を用いると、答えは$$~~~\sqrt{3}\sin{\theta}-\cos{\theta}=2\sin{\left(\theta-\frac{\pi}{6}\right)}$$となります。
問題解説(3)
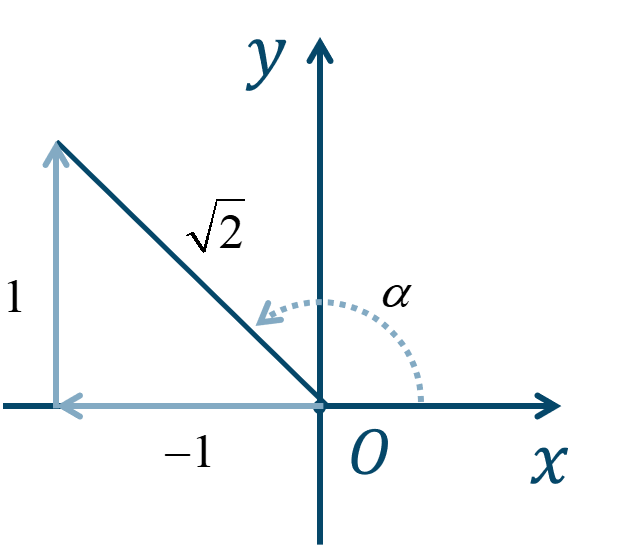
与式を、$$~~~-\sin{\theta}+\cos{\theta}$$と式変形しておきます。$$~~~~~~\sqrt{(-1)^2+1^2}$$$$~=\sqrt{1+1}$$$$~=\sqrt{2}$$これと、次の図より、
$$~~~\alpha=\frac{3}{4}\pi$$となります。
よって、合成の公式を用いると、答えは$$~~~\cos{\theta}-\sin{\theta}=\sqrt{2}\sin{\left(\theta+\frac{3}{4}\pi\right)}$$となります。
今回のまとめ
合成の公式を用いるときは、必ず座標平面上に角を表して角の値を求めましょう。また、公式を使うために \(\sin{}\) と \(\cos{}\) の順番に注意しましょう。