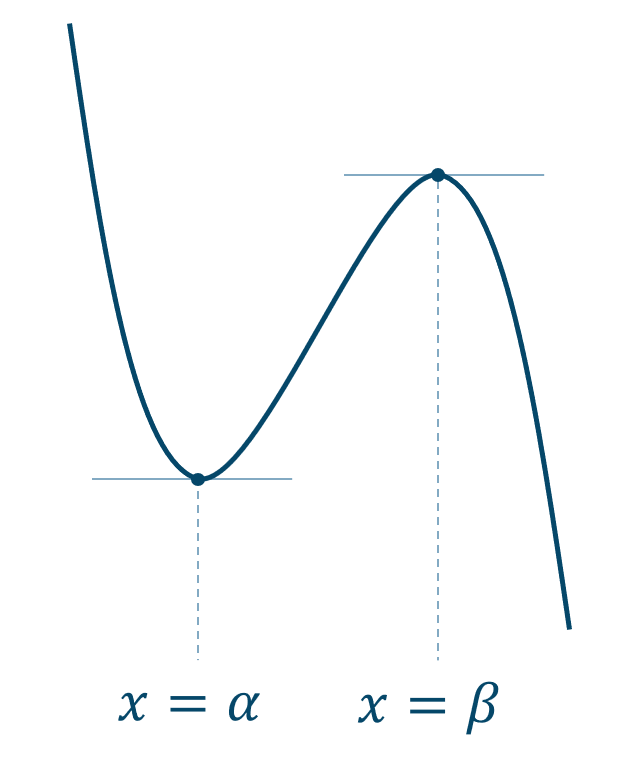3次関数のグラフと増減表
(1) ②の式より、\(f'(x)=0\) が2つの解 \(x=\alpha~,~\beta\) をもつとき、
( ⅰ ) \(a>0\) のとき、増減表は、
| \(x\) | \(\cdots\) | \(\alpha\) | \(\cdots\) | \(\beta\) | \(\cdots\) |
| \(f'(x)\) | \(+\) | \(0\) | \(-\) | \(0\) | \(+\) |
| \(f(x)\) | ↗︎ | \(f(\alpha)\) | ↘︎ | \(f(\beta)\) | ↗︎ |
グラフは、
このとき、\(f(\alpha)\) を極大値、\(f(\beta)\) を極小値といいます。
( ⅱ ) \(a<0\) のとき、増減表は、
| \(x\) | \(\cdots\) | \(\alpha\) | \(\cdots\) | \(\beta\) | \(\cdots\) |
| \(f'(x)\) | \(-\) | \(0\) | \(+\) | \(0\) | \(-\) |
| \(f(x)\) | ↘︎ | \(f(\alpha)\) | ↗︎ | \(f(\beta)\) | ↘︎ |
グラフは、
このとき、\(f(\beta)\) を極大値、\(f(\alpha)\) を極小値といいます。
(2) ②の式より \(f'(x)=0\) が1つの解 \(x=\alpha\) をもつとき、
( ⅰ ) \(a>0\) のとき、増減表は、
| \(x\) | \(\cdots\) | \(\alpha\) | \(\cdots\) |
| \(f'(x)\) | \(+\) | \(0\) | \(+\) |
| \(f(x)\) | ↗︎ | \(f(\alpha)\) | ↗︎ |
グラフは、
このとき、\(f(\alpha)\) は極値ではありません。
( ⅱ ) \(a<0\) のとき、増減表は、
| \(x\) | \(\cdots\) | \(\alpha\) | \(\cdots\) |
| \(f'(x)\) | \(-\) | \(0\) | \(-\) |
| \(f(x)\) | ↘︎ | \(f(\alpha)\) | ↘︎ |
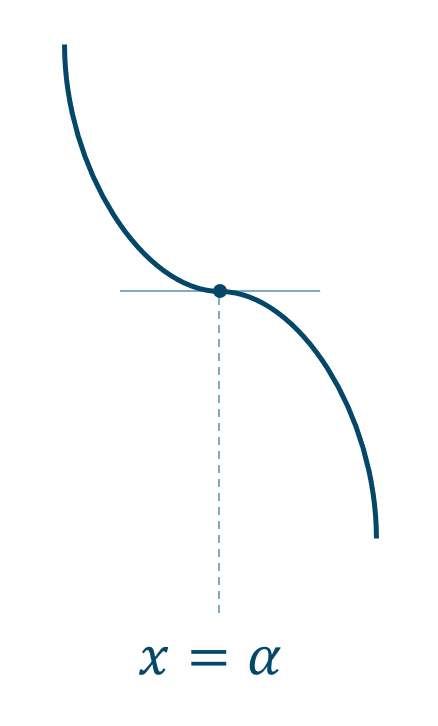
グラフは、
このとき、\(f(\alpha)\) は極値ではありません。
(3) ②の式より、\(f'(x)=0\) が解をもたないとき、
( ⅰ ) \(f'(x)\) がすべての \(x\) について常に \(f'(x)>0\) のとき、単調増加のグラフとなります。
( ⅱ ) \(f'(x)\) がすべての \(x\) について常に \(f'(x)<0\) のとき、単調減少のグラフとなります。

問題解説:3次関数のグラフと増減表
問題解説(1)
\(y\) を \(x\) で微分すると、$$\hspace{ 10 pt}y’=3x^2-12x+9$$右辺を因数分解していくと、$$\hspace{ 21 pt}=3(x^2-4x+3)$$$$\hspace{ 21 pt}=3(x-1)(x-3)$$ここで、\(y’=0\) となるのは、$$\hspace{ 20 pt}x=1~,~3$$
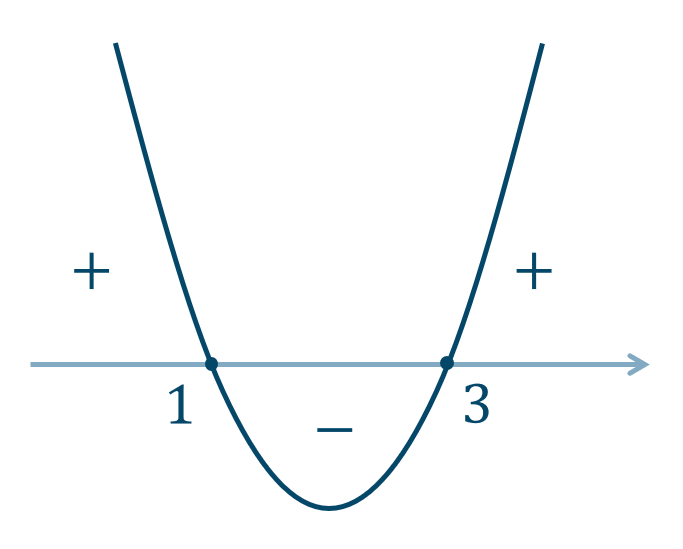
これより、\(y’\) のグラフは次のようになります。
また、\(x=1\) のとき \(y\) 座標は、$$\hspace{ 10 pt}y=1^3-6\cdot1^2+9\cdot1$$$$\hspace{ 18 pt}=1-6+9$$$$\hspace{ 18 pt}=4$$
\(x=3\) のとき \(y\) 座標は、$$\hspace{ 10 pt}y=3^3-6\cdot3^2+9\cdot3$$$$\hspace{ 18 pt}=27-54+27$$$$\hspace{ 18 pt}=0$$
以上より、\(y\) の増減表は次のようになります。
| \(x\) | \(\cdots\) | \(1\) | \(\cdots\) | \(3\) | \(\cdots\) |
| \(y’\) | \(+\) | \(0\) | \(-\) | \(0\) | \(+\) |
| \(y\) | ↗︎ | \(4\) | ↘︎ | \(0\) | ↗︎ |
よって、
\(x=1\) のとき極大値 \(4\)
\(x=3\) のとき極小値 \(0\)
グラフは次のようになります。
問題解説(2)
\(y\) を \(x\) で微分すると、$$\hspace{ 10 pt}y’=-3x^2+3x+6$$右辺を因数分解していくと、$$\hspace{ 21 pt}=-3(x^2-x-2)$$$$\hspace{ 21 pt}=-3(x+1)(x-2)$$ここで、\(y’=0\) となるのは、$$\hspace{ 20 pt}x=-1~,~2$$
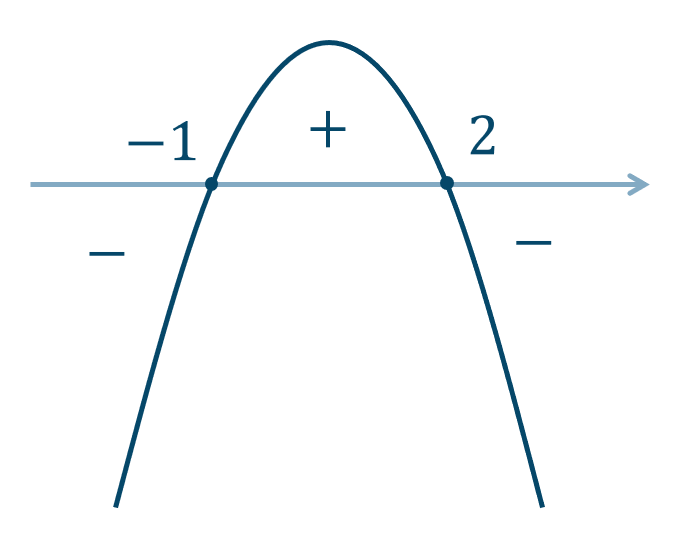
これより、\(y’\) のグラフは次のようになります。
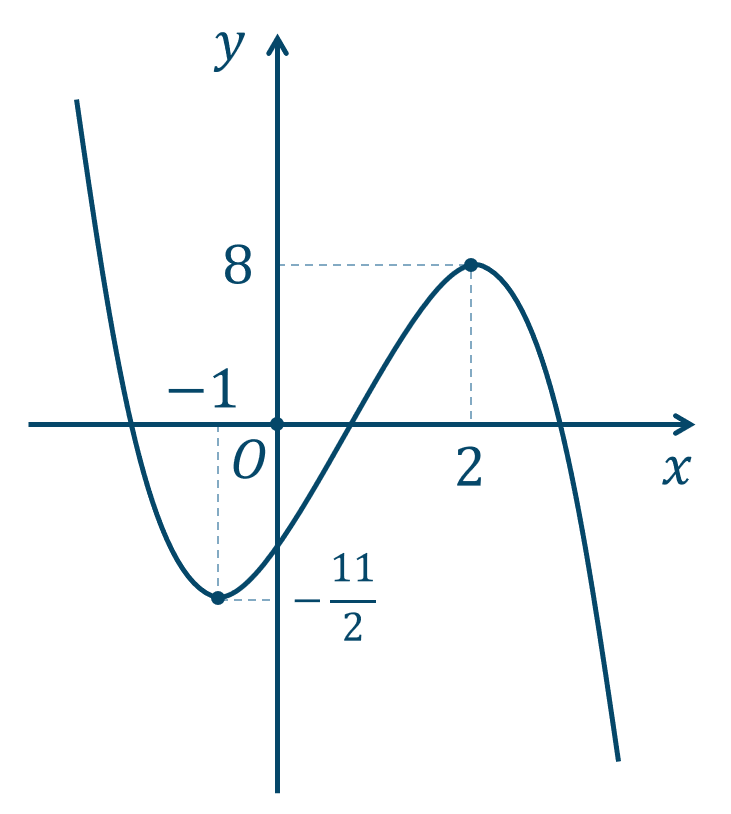
また、\(x=-1\) のとき \(y\) 座標は、$$\hspace{ 10 pt}y=-(-1)^3+\frac{3}{2}(-1)^2+6(-1)-2$$$$\hspace{ 18 pt}=1+\frac{3}{2}-6-2$$$$\hspace{ 18 pt}=\frac{3}{2}-7$$$$\hspace{ 18 pt}=\frac{3-14}{2}$$$$\hspace{ 18 pt}=-\frac{11}{2}$$
\(x=2\) のとき \(y\) 座標は、$$\hspace{ 10 pt}y=-2^3+\frac{3}{2}\cdot2^2+6\cdot2-2$$$$\hspace{ 18 pt}=-8+6+12-2$$$$\hspace{ 18 pt}=8$$
以上より、\(y\) の増減表は次のようになります。
| \(x\) | \(\cdots\) | \(-1\) | \(\cdots\) | \(2\) | \(\cdots\) |
| \(y’\) | \(-\) | \(0\) | \(+\) | \(0\) | \(-\) |
| \(y\) | ↘︎ | \(-{\large \frac{11}{2}}\) | ↗︎ | \(8\) | ↘︎ |
よって、
\(x=2\) のとき極大値 \(8\)
\(x=-1\) のとき極小値 \(-{\large \frac{11}{2}}\)
グラフは次のようになります。
問題解説(3)
\(y\) を \(x\) で微分すると、$$\hspace{ 10 pt}y’=-6x^2+12x-6$$右辺を因数分解していくと、$$\hspace{ 21 pt}=-6(x^2-2x+1)$$$$\hspace{ 21 pt}=-6(x-1)^2$$ここで、\(y’=0\) となるのは、$$\hspace{ 20 pt}x=1$$
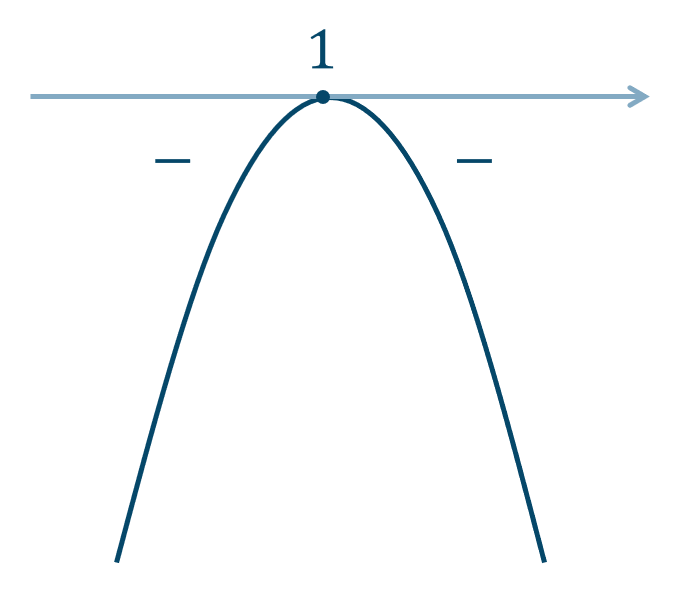
これより、\(y’\) のグラフは次のようになります。
また、\(x=1\) のときの \(y\) 座標は$$\hspace{ 10 pt}y=-2\cdot1^3+6\cdot1^2-6\cdot1+1$$$$\hspace{ 18 pt}=-2+6-6+1$$$$\hspace{ 18 pt}=-1$$
以上より、\(y\) の増減表は次のようになります。
| \(x\) | \(\cdots\) | \(1\) | \(\cdots\) |
| \(y’\) | \(-\) | \(0\) | \(-\) |
| \(y\) | ↘︎ | \(-1\) | ↘︎ |
グラフは次のようになります。
問題解説(4)
\(y\) を \(x\) で微分すると、$$\hspace{ 10 pt}y’=3x^2+5$$よって、すべての \(x\) について、$$\hspace{ 10 pt}y’=3x^2+5>0$$であるので、常に \(y’>0\) となり、\(y\) は単調増加のグラフとなります。
また、\(x=0\) のとき \(y\) 座標は$$\hspace{ 10 pt}y=0^3+5\cdot0$$$$\hspace{ 18 pt}=0$$
よって、グラフは次のようになります。
今回のまとめ
3次関数のグラフを描くときは、\(y’=0\) の解の個数と \(x^3\) の係数の正負によって場合分けされることをしっかりと覚えておきましょう。