指数関数と対数関数の極限の解法
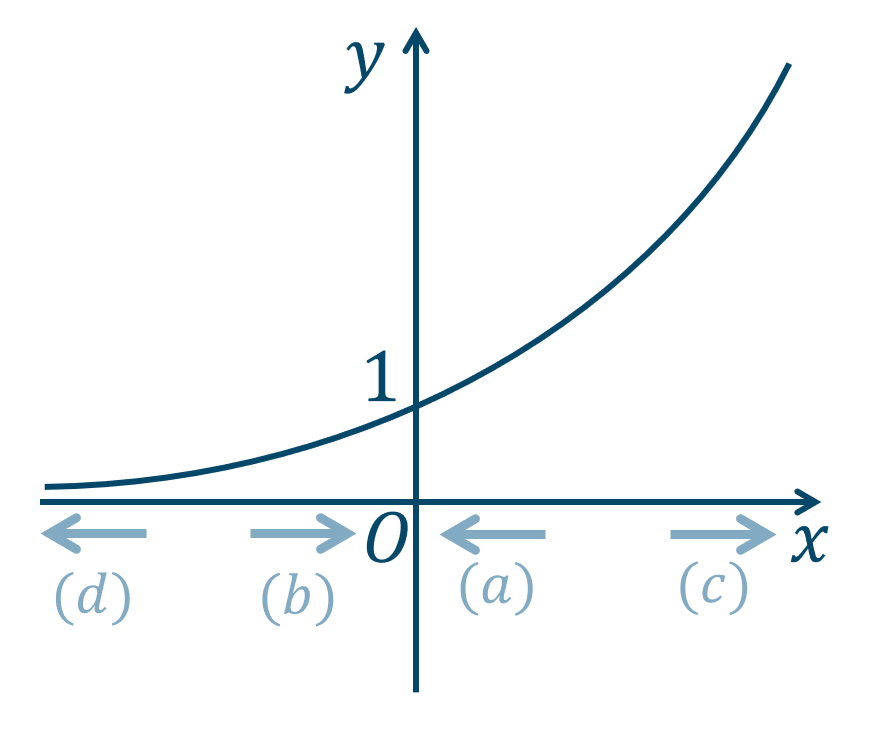
\((a)~x\to +0\) のときは、
\(x\) 軸の正の部分から \(x=0\) に近づいたときの \(y\) の値を考えます。
\((b)~x\to -0\) のときは、
\(x\) 軸の負の部分から \(x=0\) に近づいたときの \(y\) の値を考えます。
\((c)~x\to \infty\) のときは、
\(x\) 軸の \(+\infty\) に発散したときの \(y\) の値を考えます。
\((d)~x\to -\infty\) のときは、
\(x\) 軸の \(-\infty\) に発散したときの \(y\) の値を考えます。
問題解説:指数関数と対数関数の極限①
問題解説(1)
\({\small (1)}~\)関数 \(f(x)=3^x\) について、次の極限を求めよ。$$~{\large ①}~ \lim_{x\to+0}f(x)~~~~~~{\large ②}~ \lim_{x\to-0}f(x)$$$$~{\large ③}~ \lim_{x\to \infty}f(x)~~~~~~~{\large ④}~ \lim_{x\to-\infty}f(x)$$
\(f(x)=3^x\) のグラフは次のようになります。
したがって、答えは
\((a)\)より、\(y\to 1\) となるので、$$~{\large ①}~\lim_{x\to +0}3^x=1$$\((b)\)より、\(y\to 1\) となるので、$$~{\large ②}~\lim_{x\to -0}3^x=1$$\((c)\)より、\(y\to \infty\) となるので、$$~{\large ③}~\lim_{x\to \infty}3^x=\infty$$\((d)\)より、\(y\to 0\) となるので、$$~{\large ④}~\lim_{x\to -\infty}3^x=0$$
問題解説(2)
\({\small (2)}~\)関数 \(f(x)= \left({\large \frac{1}{3}}\right)^x\) について、次の極限を求めよ。$$~{\large ①}~ \lim_{x\to+0}f(x)~~~~~~{\large ②}~\lim_{x\to-0}f(x)$$$$~{\large ③}~ \lim_{x\to \infty}f(x)~~~~~~~{\large ④}~ \lim_{x\to-\infty}f(x)$$
\(f(x)=\left({\large \frac{1}{3}}\right)^x\) のグラフは次のようになります。
したがって、答えは
\((a)\)より、\(y\to 1\) となるので、$$~{\large ①}~\lim_{x\to +0}\left(\frac{1}{3}\right)^x=1$$\((b)\)より、\(y\to 1\) となるので、$$~{\large ②}~\lim_{x\to -0}\left(\frac{1}{3}\right)^x=1$$\((c)\)より、\(y\to 0\) となるので、$$~{\large ③}~\lim_{x\to \infty}\left(\frac{1}{3}\right)^x=0$$\((d)\)より、\(y\to \infty\) となるので、$$~{\large ④}~\lim_{x\to -\infty}\left(\frac{1}{3}\right)^x=\infty$$
問題解説(3)
\({\small (3)}~\)関数 \(f(x)= \log_{3}{x}\) について、次の極限を求めよ。$$~{\large ①}~ \lim_{x\to+0}f(x)~~~~~~{\large ②}~ \lim_{x\to \infty}f(x)$$
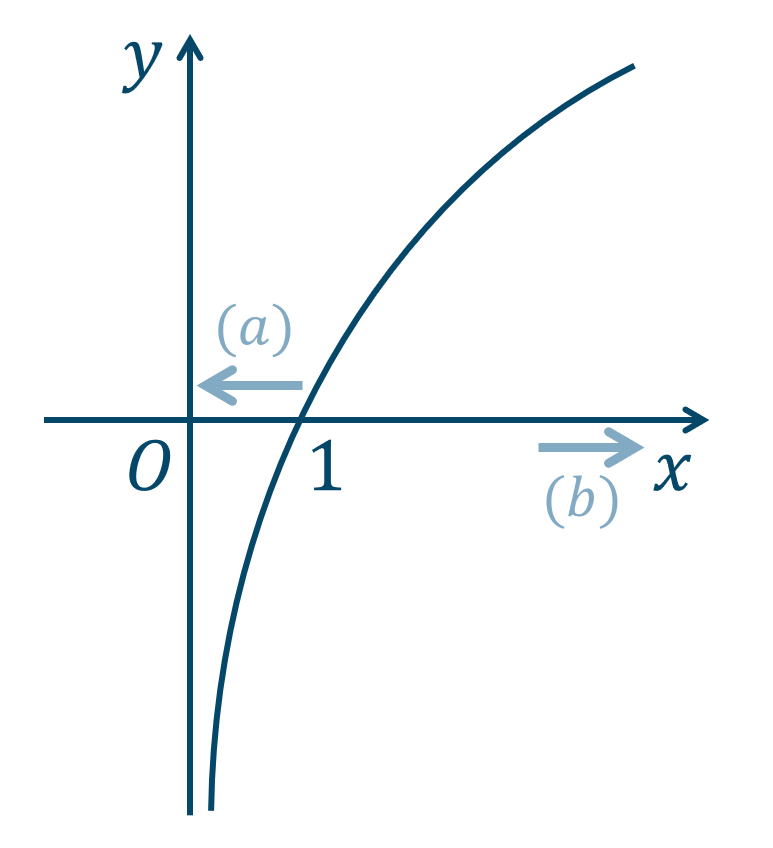
\(f(x)=\log_{3}{x}\) のグラフは次のようになります。
したがって、答えは
\((a)\)より、\(y\to -\infty\) となるので、$$~{\large ①}~\lim_{x\to +0}\log_{3}{x}=-\infty$$\((b)\)より、\(y\to \infty\) となるので、$$~{\large ②}~\lim_{x\to \infty}\log_{3}{x}=\infty$$
問題解説(4)
\({\small (4)}~\)関数 \(f(x)= \log_{\frac{1}{3}}{x}\) について、次の極限を求めよ。$$~{\large ①}~ \lim_{x\to+0}f(x)~~~~~~{\large ②}~ \lim_{x\to \infty}f(x)$$
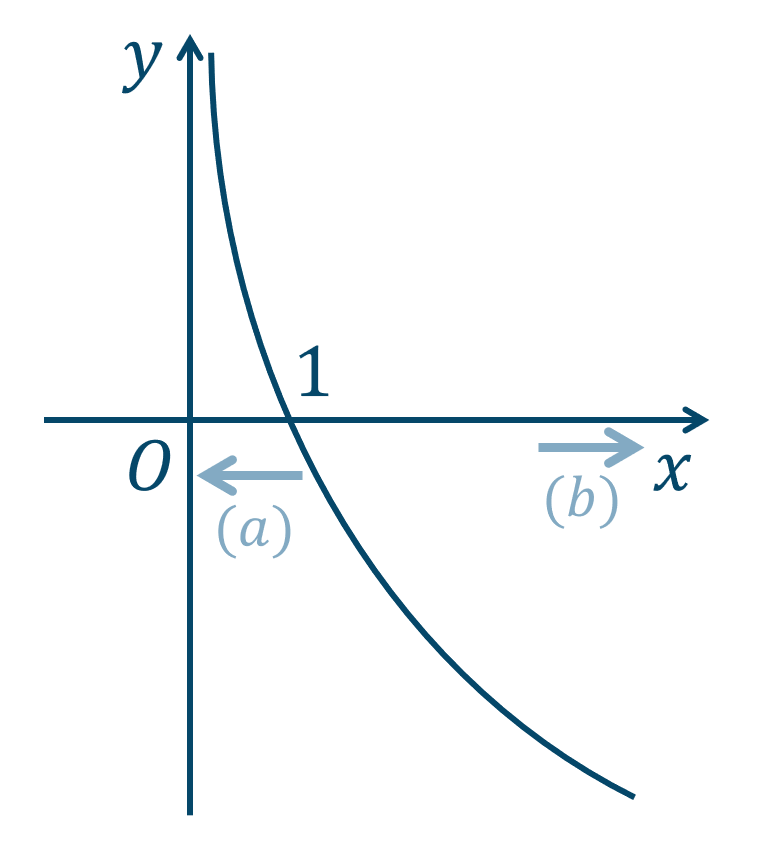
\(f(x)=\log_{\frac{1}{3}}{x}\) のグラフは次のようになります。
したがって、答えは
\((a)\)より、\(y\to \infty\) となるので、$$~{\large ①}~\lim_{x\to +0}\log_{\frac{1}{3}}{x}=\infty$$\((b)\)より、\(y\to -\infty\) となるので、$$~{\large ②}~\lim_{x\to \infty}\log_{\frac{1}{3}}{x}=-\infty$$
今回のまとめ
指数関数と対数関数の基本的な極限の求め方は、それぞれのグラフを描いて考えましょう。