チェバの定理

2018.10.182020.06.09

チェバの定理の解法
問題解説：チェバの定理
今回のまとめ

チェバの定理の解法

Point：チェバの定理解法の手順は、
① 着目する三角形を決めます。
次の図の $\triangle {\rm ABC}$ に着目する。

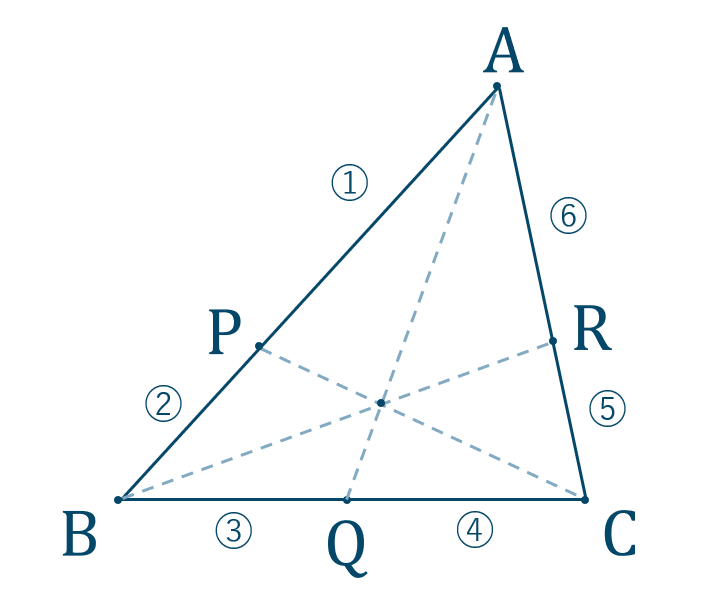
② 頂点 ${\rm A}$ $,$ ${\rm B}$ $,$ ${\rm C}$ と交点 ${\rm P}$ $,$ ${\rm Q}$ $,$ ${\rm R}$ を確認して、頂点→交点→頂点→…と進んでいくルートを決めます。$$~~~{\rm A}~\to~{\rm P}~\to~{\rm B}~\to~{\rm Q}~\to~{\rm C}~\to~{\rm R}~\to~{\rm A}$$③ チェバの定理より式を立てます。

$$\frac{{\rm AP}}{{\rm PB}}\times \frac{{\rm BQ}}{{\rm QC}}\times \frac{{\rm CR}}{{\rm RA}}=1$$

問題解説：チェバの定理

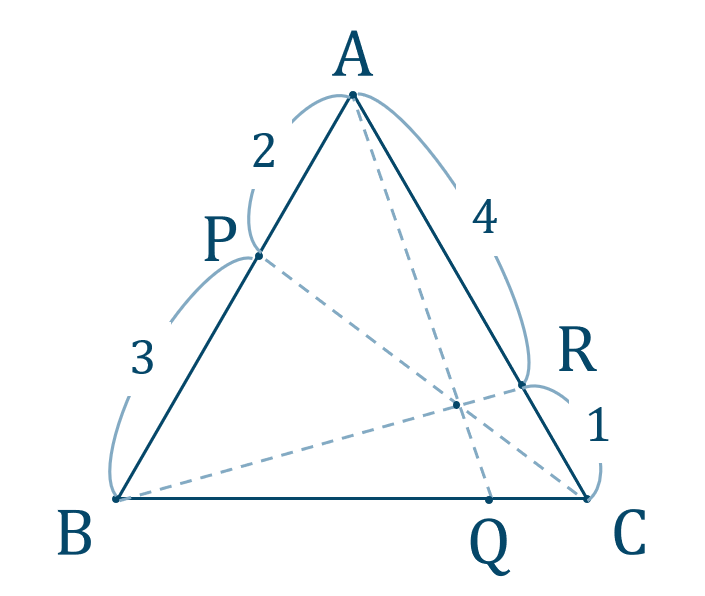
問題次の $\triangle {\rm ABC}$ について、${\rm AB}={\rm BC}={\rm CA}=5$ $,$ ${\rm AP}=2$ $,$ ${\rm AR}=4$ のとき、${\rm BQ}:{\rm QC}$ の比を求めよ。

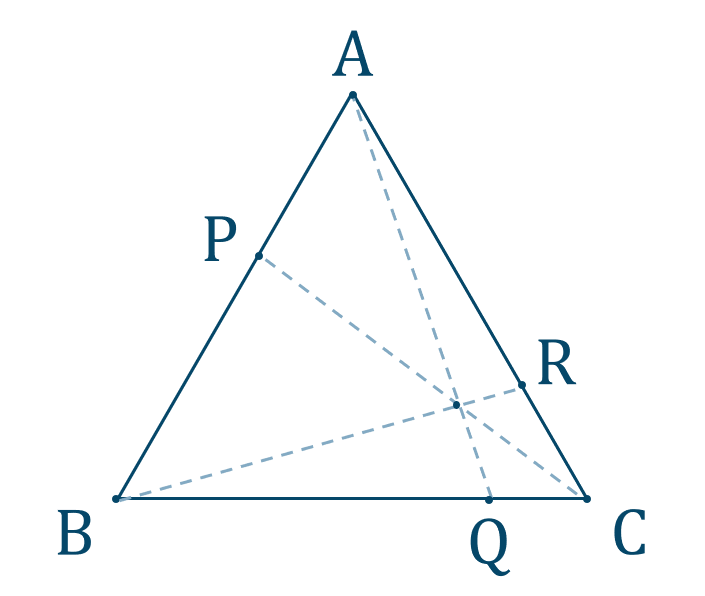
図は次のようになります。

$\triangle {\rm ABC}$ に着目して、交点が ${\rm P}$ $,$ ${\rm Q}$ $,$ ${\rm R}$ であるので、$$~~~{\rm A}~\to~{\rm P}~\to~{\rm B}~\to~{\rm Q}~\to~{\rm C}~\to~{\rm R}~\to~{\rm A}$$と進むチェバの定理より、$$\hspace{ 10 pt}\frac{{\rm AP}}{{\rm PB}}\times \frac{{\rm BQ}}{{\rm QC}}\times \frac{{\rm CR}}{{\rm RA}}=1$$これに値を代入すると、$$\hspace{ 10 pt}\frac{2}{3}\times \frac{{\rm BQ}}{{\rm QC}}\times \frac{1}{4}=1$$$$\hspace{ 32 pt}\frac{1}{6}\times \frac{{\rm BQ}}{{\rm QC}}=1$$両辺に $6$ をかけると、$$\hspace{ 10 pt}\frac{{\rm BQ}}{{\rm QC}}=\frac{6}{1}$$よって、答えは$$~~~{\rm BQ}:{\rm QC}=6:1$$となります。