三角形になるための条件
2辺の和が他の1辺より大きくなるので、
これらがすべて成り立ちます。
逆に、3つの値が3辺の長さとなる三角形となるためには、上のの3つの式がすべて成り立つ必要があります。
問題解説:三角形になるための条件
問題解説(1)
三角形の辺の条件の2辺の和は、他の1辺より大きいので、$$~~~ \begin{eqnarray} x+2>5~~~\cdots{\Large ①} \\ x+5>2~~~\cdots{\Large ②} \\ 2+5>x~~~\cdots{\Large ③} \end{eqnarray}$$
①より、$$\hspace{ 10 pt}x+2>5$$移項すると、$$\hspace{ 10 pt}x>5-2$$$$\hspace{ 10 pt}x>3$$
また、②より$$\hspace{ 10 pt}x+5>2$$移項すると、$$\hspace{ 10 pt}x>2-5$$$$\hspace{ 10 pt}x>-3$$
また、③より$$\hspace{ 10 pt}2+5>x$$$$\hspace{ 28 pt}7>x$$両辺を入れ替えると、$$\hspace{ 10 pt}x<7$$
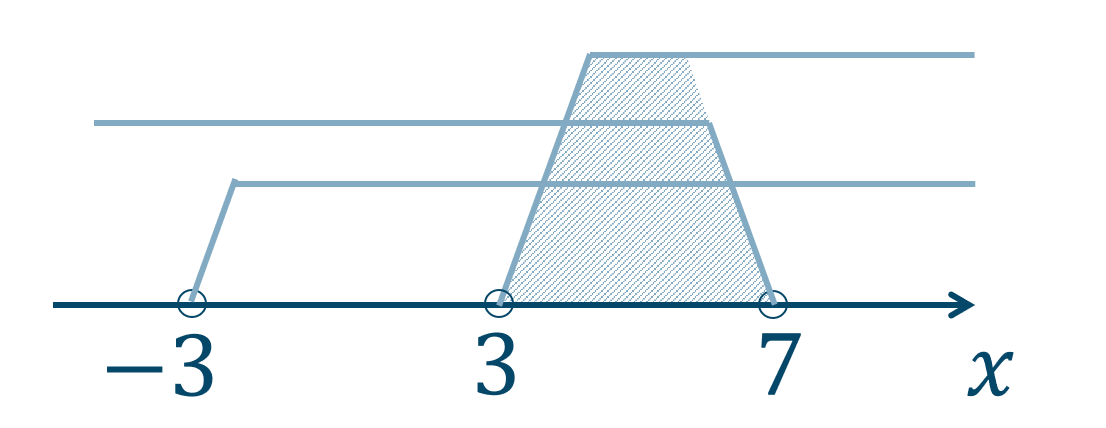
よって、数直線上にまとめると、
これより、答えは$$~~~3<x<7$$となります。
問題解説(2)
三角形の辺の条件の2辺の和は、他の1辺より大きいので、$$~~~ \begin{eqnarray} x+2x>3~~~\cdots{\Large ①} \\ x+3>2x~~~\cdots{\Large ②} \\ 2x+3>x~~~\cdots{\Large ③} \end{eqnarray}$$
①より$$\hspace{ 10 pt}x+2x>3$$$$\hspace{ 10 pt}3x>3$$両辺を \(3\) で割ると$$\hspace{ 10 pt}x>1$$
また、②より$$\hspace{ 10 pt}x+3>2x$$移項すると、$$\hspace{ 10 pt}x-2x>-3$$$$\hspace{ 26 pt}-x>-3$$両辺を \(-1\) かけると、不等号の向きが逆になるので、$$\hspace{ 10 pt}x<3$$
また、③より$$\hspace{ 10 pt}2x+3>x$$移項すると、$$\hspace{ 10 pt}2x-x>-3$$$$\hspace{ 33 pt}x>-3$$
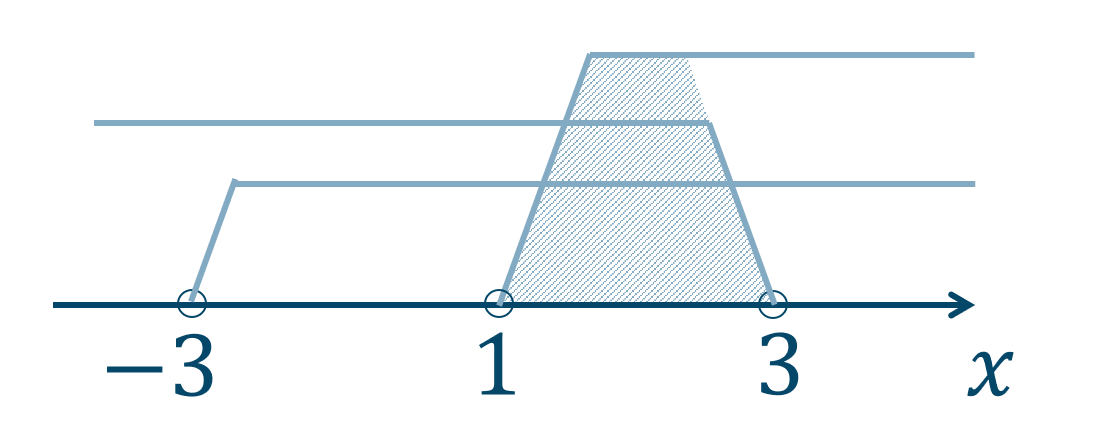
よって、数直線上にまとめると、
これより、答えは$$~~~1<x<3$$となります。
今回のまとめ
三角形になるための条件は、3つの辺より3つの条件式をつくりそれを解くことにより求めましょう。