空間ベクトルの内積①（基本）

2018.12.242020.06.09

空間ベクトルの内積の解法
問題解説：空間ベクトルの内積①（基本）
今回のまとめ

空間ベクトルの内積の解法

Point：空間ベクトルの内積始点が同じ２つのベクトル$$~~~\overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}$$において、

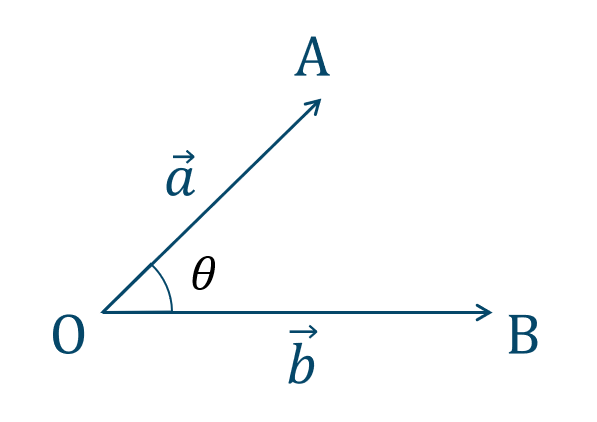
この２つのベクトルのなす角を$$~~~\theta~~~(0^\circ≦\theta≦180^\circ)$$としたとき、
$\overrightarrow{a}\cdot\overrightarrow{b}$ を $\overrightarrow{a}$ と $\overrightarrow{b}$ の内積といい次の式で表します。

$$\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos{\theta}$$

問題解説：空間ベクトルの内積①（基本）

問題解説(1)

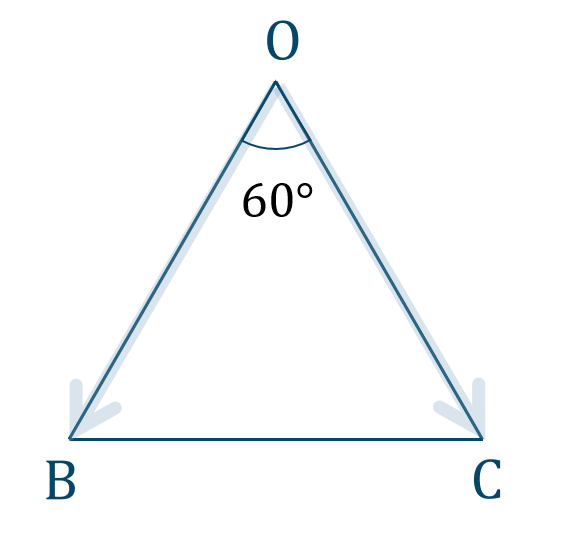
問題１辺の長さが $2$ の正四面体 ${\rm OABC}$ と線分 ${\rm AB}$ の中点 ${\rm M}$ について、次の内積を求めよ。$${\small (1)}~\overrightarrow{\rm OB}\cdot\overrightarrow{\rm OC}$$

$\triangle {\rm OAC}$ について、

$\overrightarrow{\rm OB}$ と $\overrightarrow{\rm OC}$ のなす角が $60^\circ$ であるので、内積は、$$\hspace{ 10 pt}\overrightarrow{\rm OB}\cdot\overrightarrow{\rm OC}=|\overrightarrow{\rm OB}|\cdot|\overrightarrow{\rm OC}|\cdot\cos{60^\circ}$$$$\hspace{ 50 pt}=2\cdot2\cdot\frac{1}{2}$$$$\hspace{ 50 pt}=2$$
よって、答えは$$~~~\overrightarrow{\rm OB}\cdot\overrightarrow{\rm OC}=2$$となります。

問題解説(2)

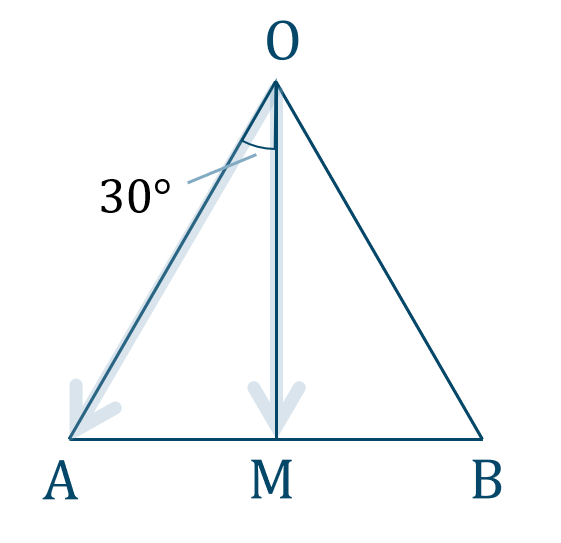
問題$${\small (2)}~\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OM}$$

$\triangle {\rm OAB}$ について、

点 ${\rm M}$ は中点であることより、$|\overrightarrow{\rm AM}|=1$ となります。
また、$\triangle {\rm OAM}$ は $1:2:\sqrt{3}$ の直角三角形より、$$~~~|\overrightarrow{\rm OM}|=\sqrt{3}~,~\angle{\rm AOM}=30^\circ$$
なす角が $30^\circ$ であるので、内積は、$$\hspace{ 10 pt}\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OM}=|\overrightarrow{\rm OA}|\cdot|\overrightarrow{\rm OM}|\cdot\cos{30^\circ}$$$$\hspace{ 53 pt}=2\cdot\sqrt{3}\cdot\frac{\sqrt{3}}{2}$$$$\hspace{ 53 pt}=3$$
よって、答えは$$~~~\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OM}=3$$となります。

問題解説(3)

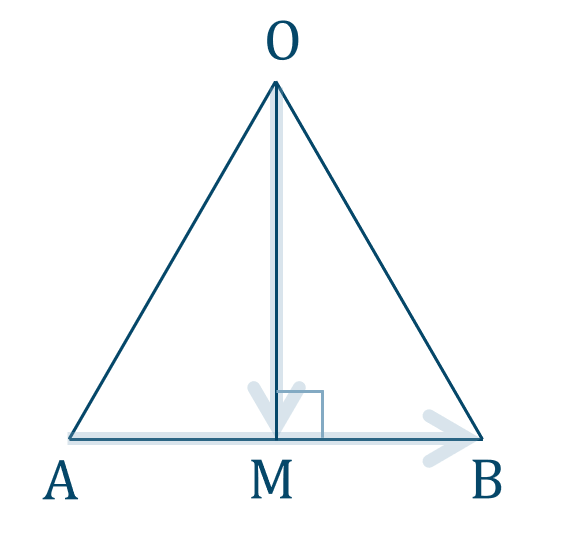
問題$${\small (3)}~\overrightarrow{\rm OM}\cdot\overrightarrow{\rm AB}$$

$\triangle {\rm OAB}$ について、

$\overrightarrow{\rm OM}$ と $\overrightarrow{\rm AB}$ のなす角が $90^\circ$ であるので、内積は、$$\hspace{ 10 pt}\overrightarrow{\rm OM}\cdot\overrightarrow{\rm AB}=|\overrightarrow{\rm OM}|\cdot|\overrightarrow{\rm AB}|\cdot\cos{90^\circ}$$$$\hspace{ 52 pt}=\sqrt{3} \cdot 2 \cdot 0$$$$\hspace{ 52 pt}=0$$
よって、答えは$$~~~\overrightarrow{\rm OM}\cdot\overrightarrow{\rm AB}=0$$となります。

問題解説(4)

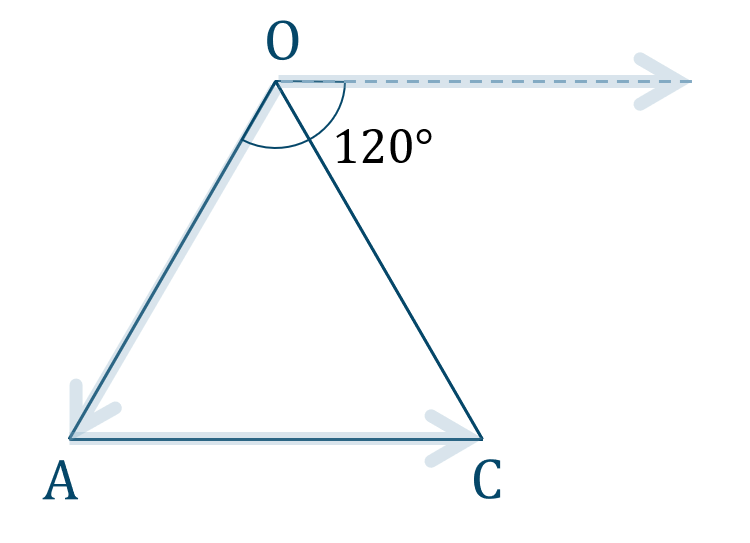
問題$${\small (4)}~\overrightarrow{\rm OA}\cdot\overrightarrow{\rm AC}$$

$\triangle {\rm OAC}$ について、

$\overrightarrow{\rm AC}$ を図のように始点が ${\rm O}$ になるように平行移動すると、$\overrightarrow{\rm OA}$ とのなす角が $120^\circ$ となります。
よって、内積は、$$\hspace{ 10 pt}\overrightarrow{\rm OA}\cdot\overrightarrow{\rm AC}=|\overrightarrow{\rm OA}|\cdot|\overrightarrow{\rm AC}|\cdot\cos{120^\circ}$$$$\hspace{ 51 pt}=2\cdot2\cdot\left(-\frac{1}{2}\right)$$$$\hspace{ 51 pt}=-2$$
よって、答えは$$~~~\overrightarrow{\rm OA}\cdot\overrightarrow{\rm AC}=-2$$となります。