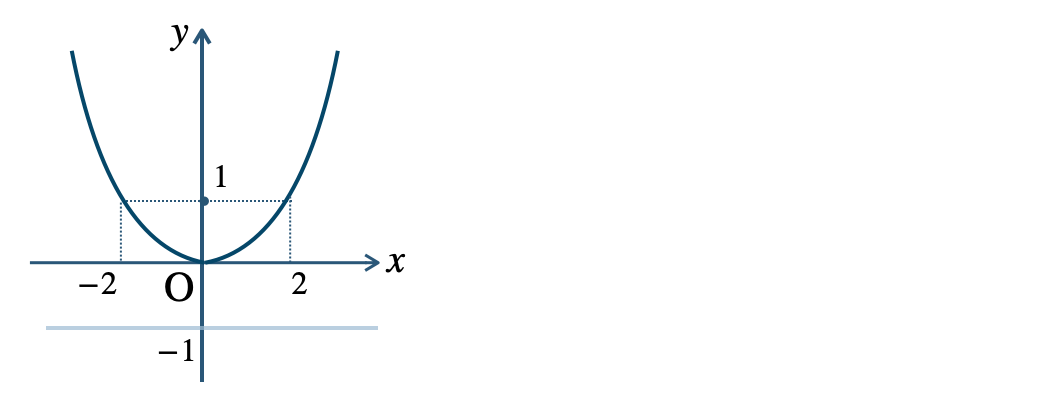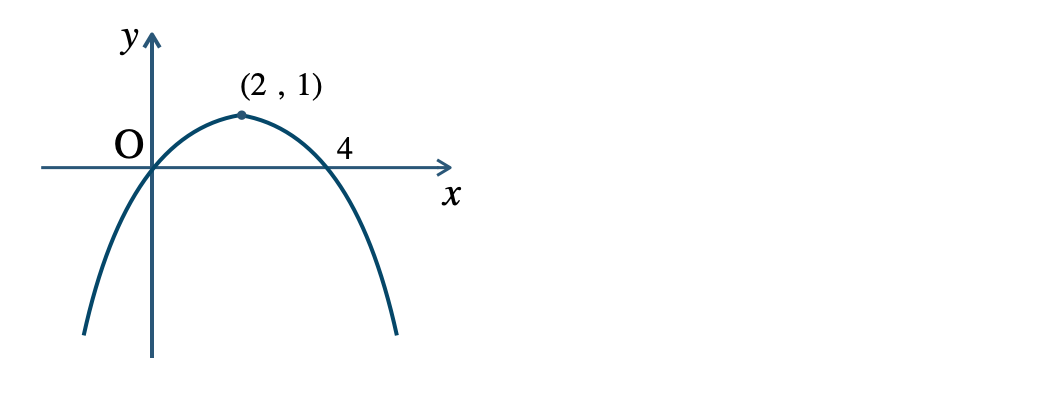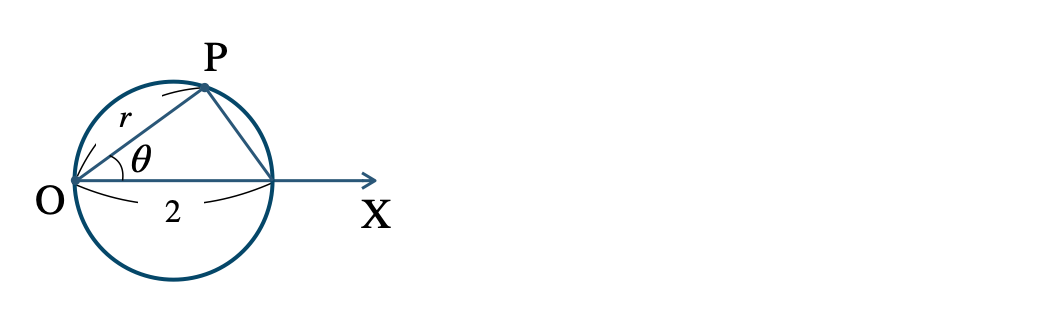【新課程】数研出版：高等学校数学Ｃ[709]

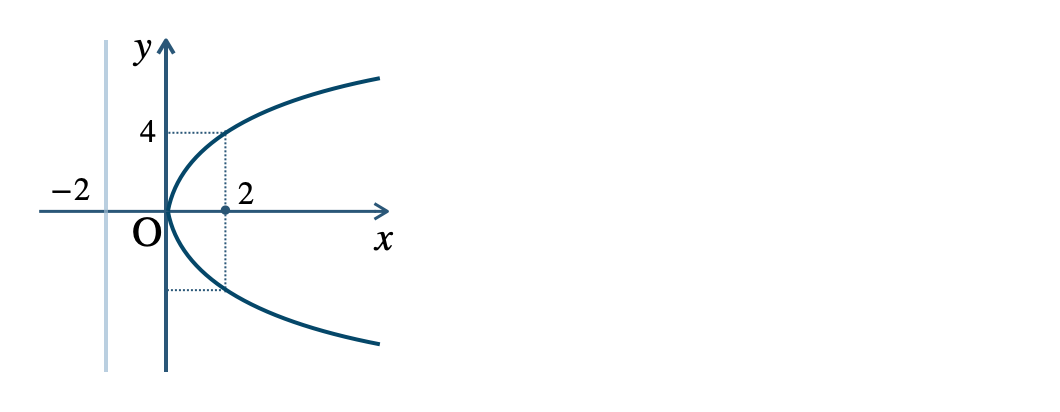
p.107 練習1\({\small (1)}~\)焦点 \((2~,~0)\)、準線 \(x=-2\)

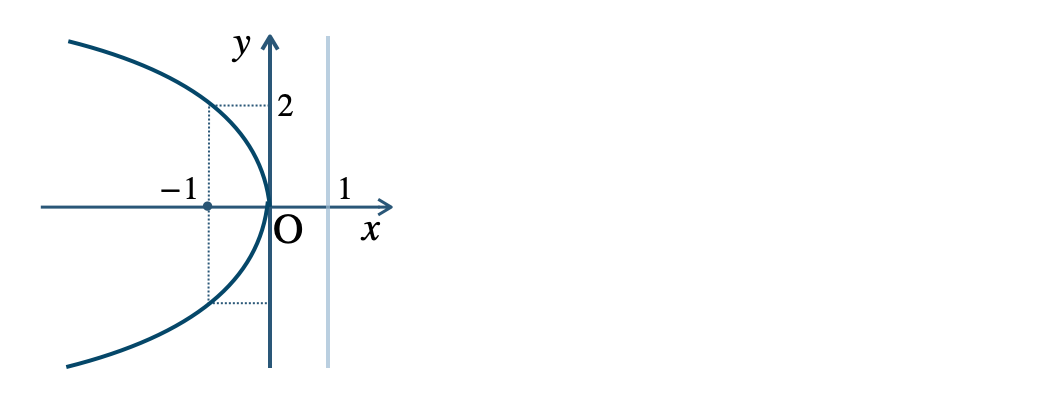
\({\small (2)}~\)焦点 \((-1~,~0)\)、準線 \(x=1\)

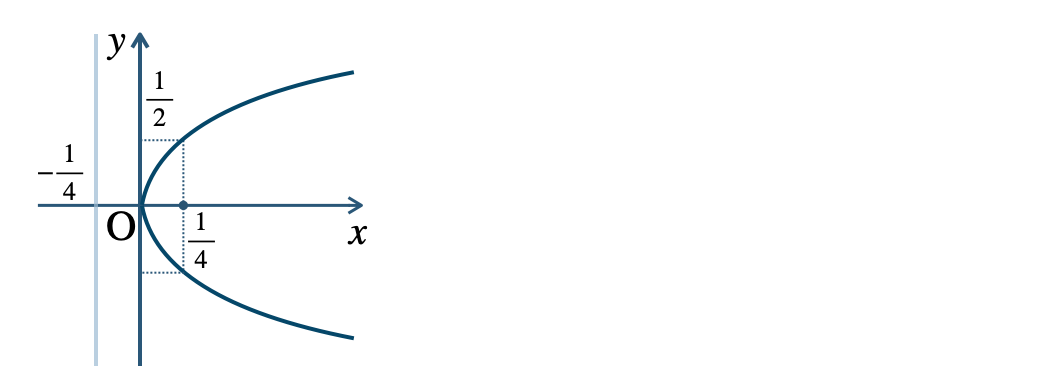
\({\small (3)}~\)焦点 \(\left({\Large \frac{\,1\,}{\,4\,}}~,~0\right)\)、準線 \(x=-{\Large \frac{\,1\,}{\,4\,}}\)

p.107 練習2$$~~~y^2=-8x$$

p.107 練習3\({\small (1)}~\)焦点 \((0~,~1)\)、準線 \(y=-1\)

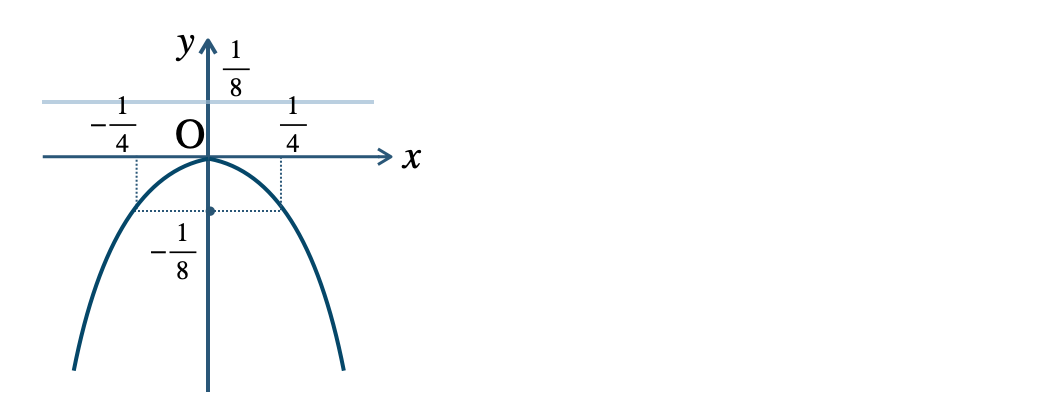
\({\small (2)}~\)焦点 \(\left(0~,~-{\Large \frac{\,1\,}{\,8\,}}\right)\)、準線 \(y={\Large \frac{\,1\,}{\,8\,}}\)

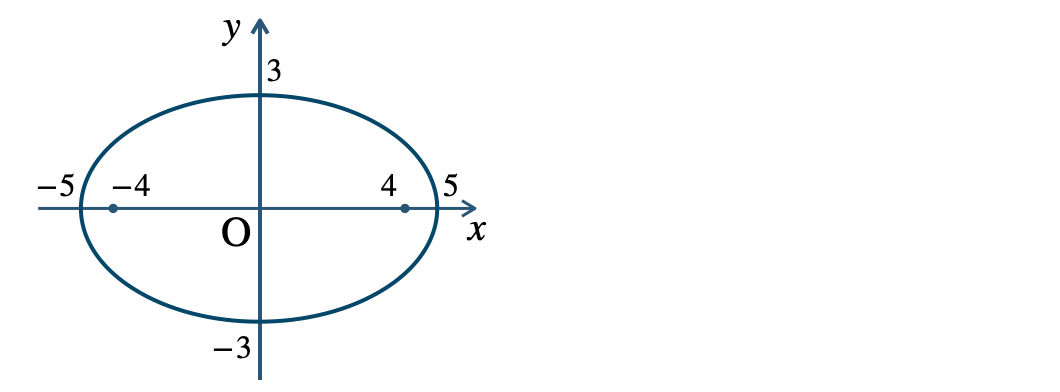
p.109 練習4\({\small (1)}~\)長軸 \(10\)、短軸 \(6\)
焦点 \((4~,~0)~,~(-4~,~0)\)

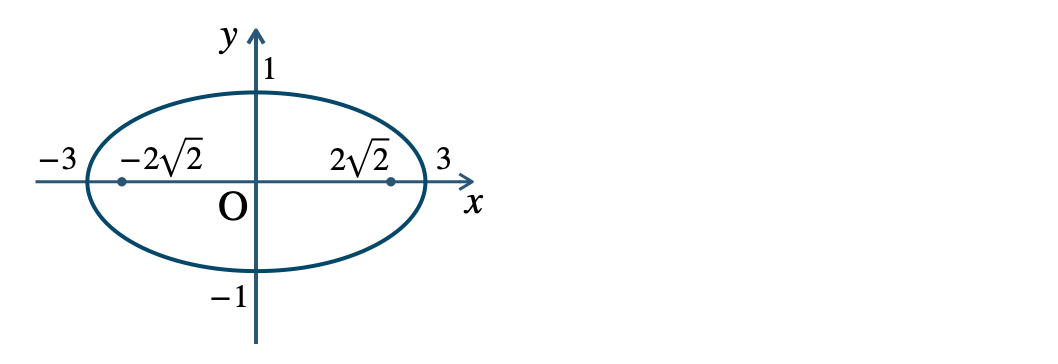
\({\small (2)}~\)長軸 \(6\)、短軸 \(2\)
焦点 \((2\sqrt{2}~,~0)~,~(-2\sqrt{2}~,~0)\)

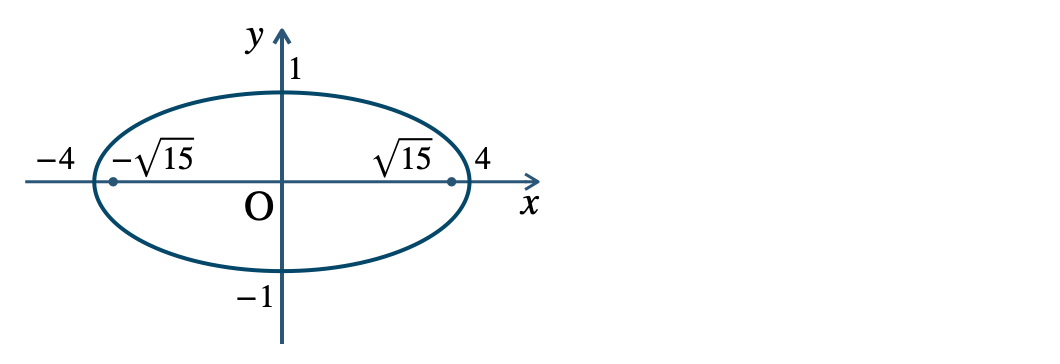
\({\small (3)}~\)長軸 \(8\)、短軸 \(2\)
焦点 \((\sqrt{15}~,~0)~,~(-\sqrt{15}~,~0)\)

p.110 練習5$$~~~\frac{\,x^2\,}{\,4\,}+y^2=1$$

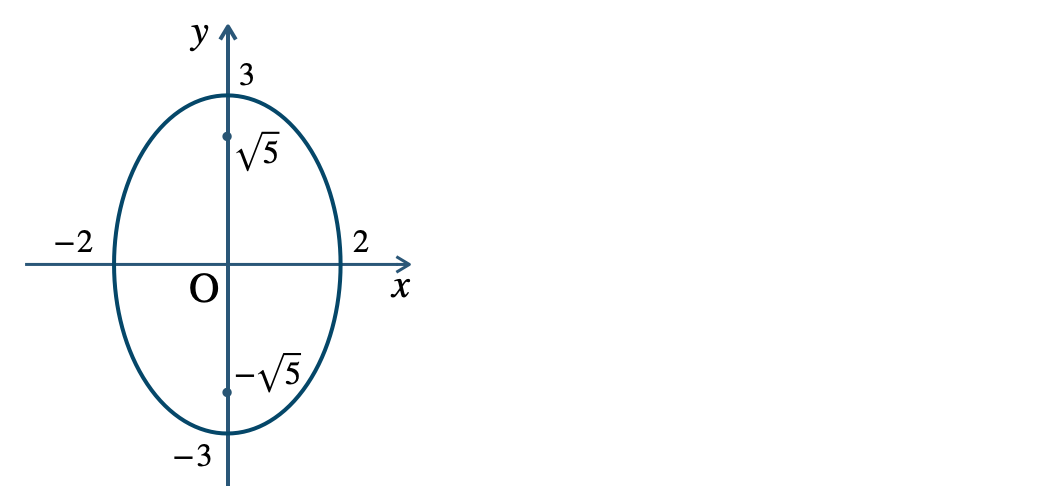
p.111 練習6\({\small (1)}~\)長軸 \(6\)、短軸 \(4\)
焦点 \((0~,~\sqrt{5})~,~(0~,~-\sqrt{5})\)

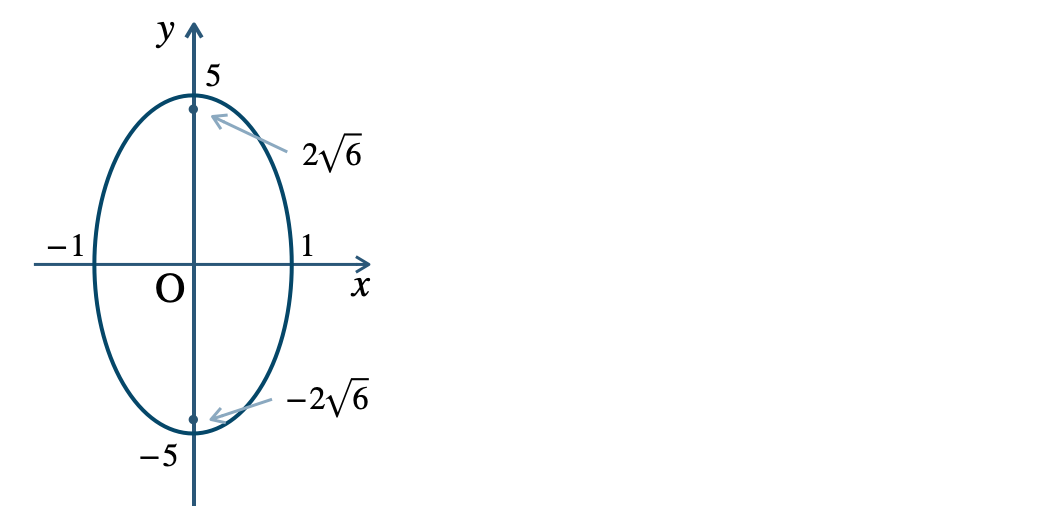
\({\small (2)}~\)長軸 \(10\)、短軸 \(2\)
焦点 \((0~,~2\sqrt{6})~,~(0~,~-2\sqrt{6})\)

p.112 練習7$${\small (1)}~\frac{\,x^2\,}{\,9\,}+\frac{\,x^2\,}{\,4\,}=1$$$${\small (2)}~\frac{\,x^2\,}{\,9\,}+\frac{\,x^2\,}{\,16\,}=1$$

p.113 練習8楕円$$~~~\frac{\,x^2\,}{\,16\,}+\frac{\,x^2\,}{\,9\,}=1$$

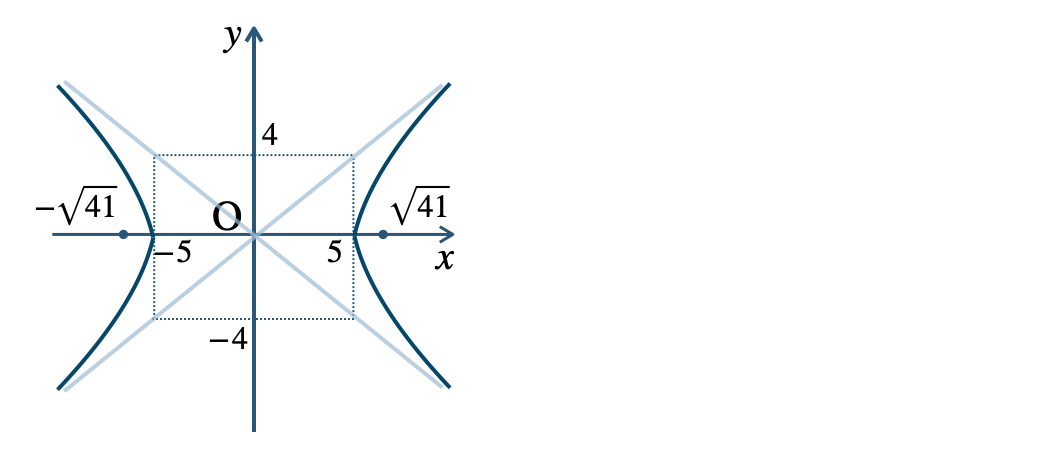
p.116 練習9\({\small (1)}~\)焦点 \((\sqrt{41}~,~0)~,~(-\sqrt{41}~,~0)\)
頂点 \((5~,~0)~,~(-5~,~0)\)
漸近線$$~~~y=\frac{\,4\,}{\,5\,}x~,~y=-\frac{\,4\,}{\,5\,}x$$

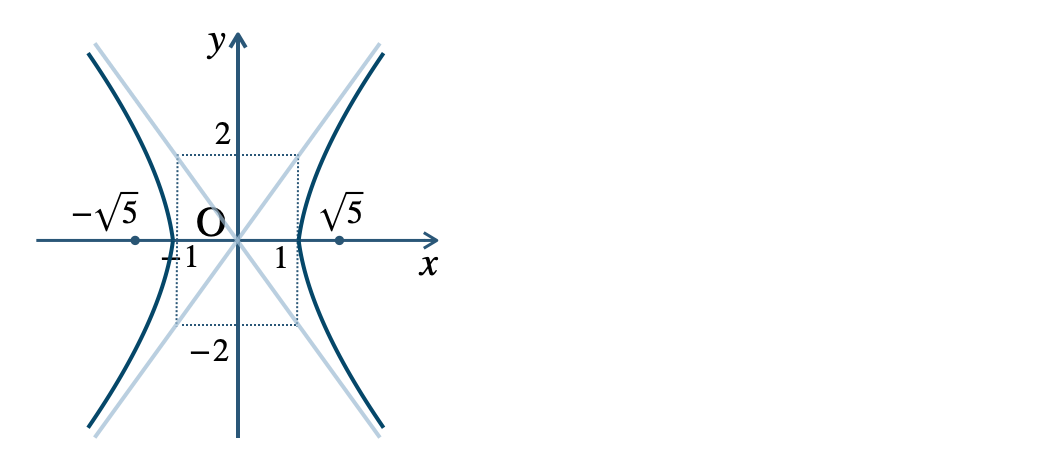
\({\small (2)}~\)焦点 \((\sqrt{5}~,~0)~,~(-\sqrt{5}~,~0)\)
頂点 \((1~,~0)~,~(-1~,~0)\)
漸近線$$~~~y=2x~,~y=-2x$$

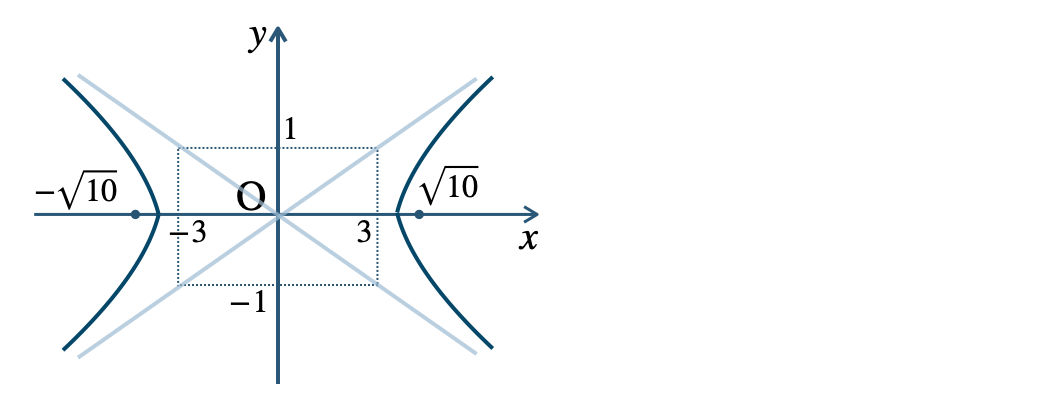
\({\small (3)}~\)焦点 \((\sqrt{10}~,~0)~,~(-\sqrt{10}~,~0)\)
頂点 \((3~,~0)~,~(-3~,~0)\)
漸近線$$~~~y=\frac{\,1\,}{\,3\,}x~,~y=-\frac{\,1\,}{\,3\,}x$$

p.117 練習10$$~~~\frac{\,x^2\,}{\,16\,}-\frac{\,y^2\,}{\,9\,}=1$$

p.117 練習11$$~~~\frac{\,x^2\,}{\,2\,}-\frac{\,y^2\,}{\,2\,}=1$$

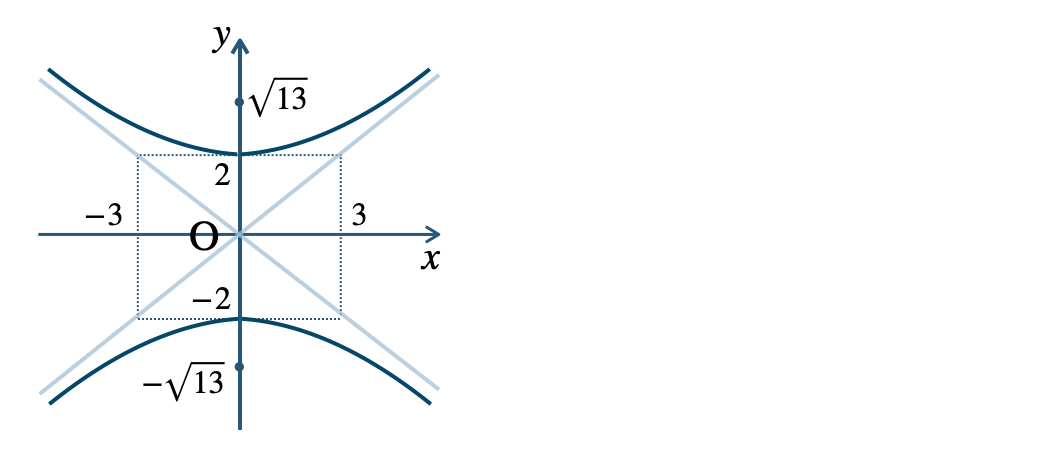
p.118 練習12\({\small (1)}~\)焦点 \((0~,~\sqrt{13})~,~(0~,~-\sqrt{13})\)
頂点 \((0~,~2)~,~(0~,~-2)\)
漸近線$$~~~y=\frac{\,2\,}{\,3\,}x~,~y=-\frac{\,2\,}{\,3\,}x$$

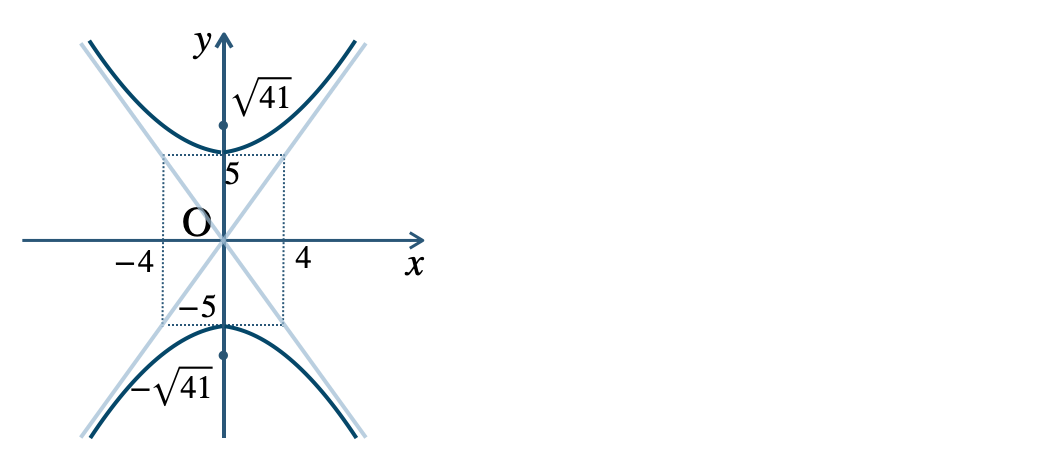
\({\small (2)}~\)焦点 \((0~,~\sqrt{41})~,~(0~,~-\sqrt{41})\)
頂点 \((0~,~5)~,~(0~,~-5)\)
漸近線$$~~~y=\frac{\,5\,}{\,4\,}x~,~y=-\frac{\,5\,}{\,4\,}x$$

p.121 練習13$$~~~\frac{\,(x-3)^2\,}{\,4\,}+(y+2)^2=1$$　焦点 \((\sqrt{3}+3~,~-2)~,~(-\sqrt{3}+3~,~-2)\)

p.121 練習14$$~~~(y-2)^2=4(x+1)$$　焦点 \((0~,~2)\)

p.122 練習15\({\small (1)}~\)楕円 \({\Large \frac{\,x^2\,}{\,4\,}}+y^2=1\) を \(x\) 軸方向に \(-2\)、

---

　\(y\) 軸方向に \(1\) だけ平行移動させた楕円

---

\({\small (2)}~\)放物線 \(y^2=16x\) を \(x\) 軸方向に \(-1\)、
　\(y\) 軸方向に \(-4\) だけ平行移動させた放物線

---

\({\small (3)}~\)双曲線 \({\Large \frac{\,x^2\,}{\,9\,}}-{\Large \frac{\,y^2\,}{\,4\,}}=1\) を \(x\) 軸方向に \(2\)、

---

　\(y\) 軸方向に \(-2\) だけ平行移動させた双曲線

p.123 練習16　\(k< -\sqrt{2}~,~\sqrt{2}< k\) のとき、２個

---

　\(k=\pm \sqrt{2}\) のとき、１個

---

　\(-\sqrt{2}< k< \sqrt{2}\) のとき、０個

p.124 練習17$$~~~y=\frac{\,1\,}{\,2\,}x-2~,~(-4~,~-4)$$$$~~~y=-\frac{\,1\,}{\,2\,}x+2~,~(-4~,~4)$$

p.125 研究 練習1$${\small (1)}~y=x+1$$$${\small (2)}~x+y=4$$

p.127 練習18[証明] 点 \({\rm P}\) の座標を \((x~,~y)\) とすると、$$~~~{\rm PF}=\sqrt{(x-4)^2+y^2}$$また、点 \({\rm P}\) から直線 \(x=1\) に下ろした点を \({\rm H}\) とすると、$$~~~{\rm PH}=|x-1|$$\({\rm PF:PH}=2:1\) であるので、$$\begin{eqnarray}~~~\sqrt{(x-4)^2+y^2}&=&2|x-1|
\\[2pt]~~~(x-4)^2+y^2&=&4(x-1)^2
\\[2pt]~~~3x^2-y^2&=&12
\\[3pt]~~~\frac{\,x^2\,}{\,4\,}-\frac{\,y^2\,}{\,12\,}&=&1
\end{eqnarray}$$よって、条件を満たす点 \({\rm P}\) は双曲線上にある
逆に、双曲線上の任意の点は条件を満たす
したがって、

---

点 \({\rm P}\) の軌跡は \({\Large \frac{\,x^2\,}{\,4\,}}-{\Large \frac{\,y^2\,}{\,12\,}}=1\) [終]

---

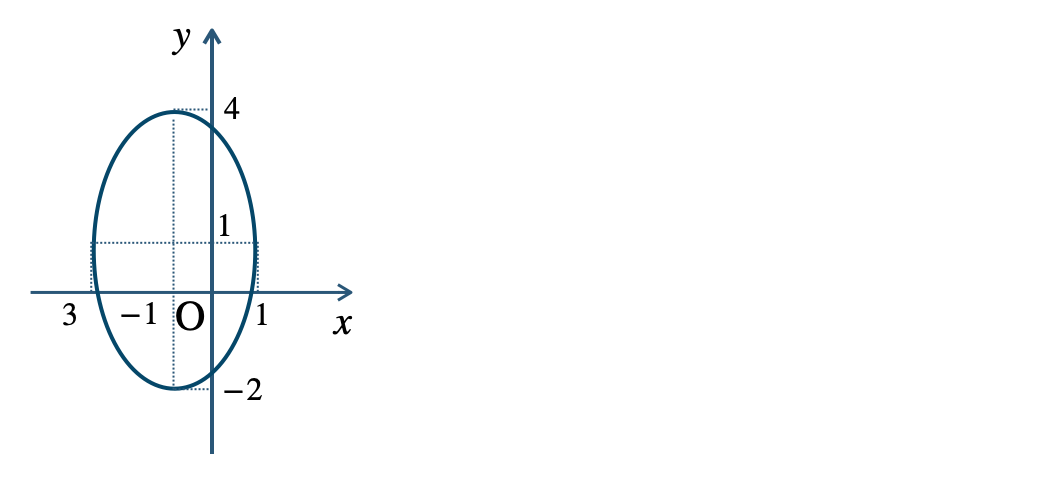
p.128 問題 3$$~~~\frac{\,(x+1)^2\,}{\,4\,}+\frac{\,(y-1)^2\,}{\,9\,}=1$$焦点 \((-1~,~\sqrt{5}+1)~,~(-1~,~-\sqrt{5}+1)\)

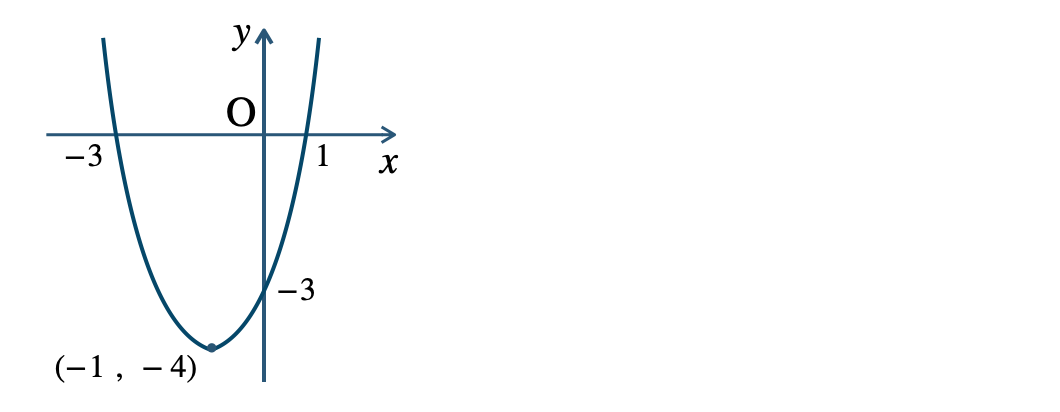
p.132 練習19$${\small (1)}~y=x^2+2x-3$$

$${\small (2)}~y=-\frac{\,1\,}{\,4\,}x^2+x$$

p.132 練習20放物線$$~~~y=x^2+x$$

p.133 練習21$${\small (1)}~x=2\cos{\theta}~,~y=2\sin{\theta}$$$${\small (2)}~x=\sqrt{2}\cos{\theta}~,~y=\sqrt{2}\sin{\theta}$$

p.133 練習22$${\small (1)}~x=3\cos{\theta}~,~y=2\sin{\theta}$$$${\small (2)}~x=4\cos{\theta}~,~y=5\sin{\theta}$$

p.133 練習23[証明] \(x={\Large \frac{\,3\,}{\,\cos{\theta}\,}}~,~y=2\tan{\theta}\) より、

---

$$\begin{split}&\frac{\,x^2\,}{\,3^2\,}-\frac{\,y^2\,}{\,2^2\,}
\\[3pt]~~=~&\frac{\,3^2\,}{\,3^2\cos^2{\theta}\,}-\frac{\,2^2\tan^2{\theta}\,}{\,2^2\,}
\\[3pt]~~=~&\frac{\,1\,}{\,\cos^2{\theta}\,}-\tan^2{\theta}
\\[3pt]~~=~&1+\tan^2{\theta}-\tan^2{\theta}=1\end{split}$$

---

したがって、\({\Large \frac{\,x^2\,}{\,3^2\,}}-{\Large \frac{\,y^2\,}{\,2^2\,}}=1\) を満たすので、

---

点 \({\rm P}\) は双曲線上を動く [終]

p.134 練習24$$~~~x=\frac{\,5\,}{\,\cos{\theta}\,}~,~y=4\tan{\theta}$$

p.134 練習25\({\small (1)}~\)点 \((2~,~-1)\) が中心で半径 \(3\) の円
\({\small (2)}~\)楕円$$~~~\frac{\,(x-1)^2\,}{\,9\,}+\frac{\,(y-3)^2\,}{\,4\,}=1$$

p.135 練習26$${\small (1)}~\left( \frac{\,2\,}{\,3\,}\pi-\sqrt{3}~,~1 \right)$$$${\small (2)}~(2\pi~,~4)$$$${\small (3)}~(3\pi+2~,~2)$$$${\small (4)}~(4\pi~,~0)$$

p.139 練習27$${\small (1)}~(\sqrt{3}~,~1)$$$${\small (2)}~(1~,~1)$$$${\small (3)}~(-3~,~0)$$

p.139 練習28$${\small (1)}~\left(2\sqrt{2}~,~\frac{\,\pi\,}{\,4\,} \right)$$$${\small (2)}~\left(2~,~\frac{\,2\,}{\,3\,}\pi \right)$$$${\small (3)}~\left(2~,~\frac{\,7\,}{\,6\,}\pi \right)$$

p.141 練習29$$~~~r=\frac{\,1\,}{\,\sin{\theta}\,}$$

p.141 練習30\({\small (1)}~\)

\({\small (2)}~\)

p.142 練習31[証明] 直線 \(l\) 上の点\({\rm P}\) の極座標を \((r~,~\theta)\) とすると、$$~~~{\rm OP}\cos{\angle {\rm AOP}}={\rm OA}$$ここで、\({\rm OP}=r~,~{\rm OA}=2~,~\)

---

\(\angle{\rm AOP}=\theta-{\Large \frac{\,\pi\,}{\,6\,}}\)より、

---

$$~~~r\cos{\left( \theta-\frac{\,\pi\,}{\,6\,} \right)}=2$$[終]

p.142 練習32$$~~~r^2(3-\cos{2\theta})=8$$

p.143 練習33$${\small (1)}~x+y=1$$$${\small (2)}~x^2+y^2-2y=0$$

p.144 練習34$$~~~3x^2-4x-y^2+1=0$$

p.145 練習35$$~~~r=\frac{\,2\,}{\,2+\cos{\theta}\,}$$

p.149 章末問題Ａ 6[証明] 円の中心を \({\rm C}(r_1~,~\theta_1)\)、円上の点を \({\rm P}(r~,~\theta)\) とすると、
３点 \({\rm O~,~C~,~P}\) で三角形ができるとき、\(\angle{\rm POC}=|\theta-\theta_1|\) で余弦定理より、$$~~~r^2+r_1^2-2rr_1\cos{(\theta-\theta_1)}=a^2$$これは点 \({\rm C}\) と \({\rm O}\) が一致するときや、点 \({\rm P}\) が直線 \({\rm OC}\) 上にあるときも成り立つ
逆に、点 \({\rm P}\) はこの円上の点である
したがって、円の極方程式は、$$~~~r^2+r_1^2-2rr_1\cos{(\theta-\theta_1)}=a^2$$[終]