因数分解（たすき掛け）

2018.03.172025.01.11

因数分解（たすき掛け）の解法

Point：たすき掛けの因数分解公式の使えない \(2x^2-5x+3\) の因数分解は、

① 掛けて \(2\)、掛けて \(3\) となり、たすき掛けの和が \(-5\) となる４つの数の組合せを考える。

　例えば、\(1{\, \small \times \,}2\) と \(3{\, \small \times \,}1\) を考えて、
　たすき掛け(斜めの掛け算)の和を求めると、

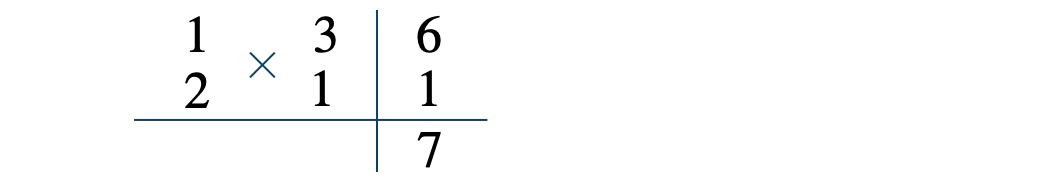
　たすき掛けの和が \(7\) となるので不適。

※ たすき掛けの和が \(x\) の係数となるように、数字や符号の組合せを変えて調べる。

　次に \(1{\, \small \times \,}2\) と \((-1){\, \small \times \,}(-3)\) を考えると、

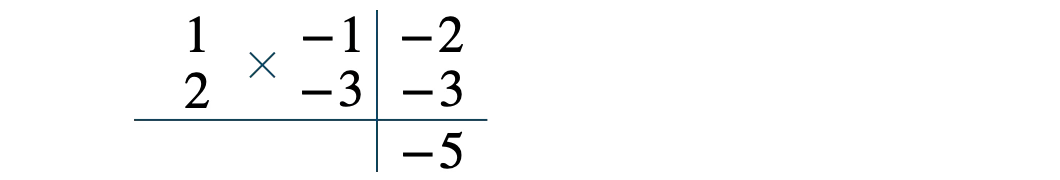
　たすき掛けの和が \(-5\) となり適する。

② これに \(x\) を付けた式が因数となる。

　上段の \(x-1\) と下段の \(2x-3\) より、
　　\(2x^2-5x+3=(x-1)(2x-3)\)

©︎ 2025 教科書より詳しい高校数学 yorikuwa.com

たすき掛けを用いる因数分解の問題演習はこちらから↓

問題次の式を因数分解せよ。

\({\small (1)}~2x^2+11x+5\)

掛けて \(2\)、掛けて \(5\) となり、たすき掛けの和が \(11\) となる４つの数の組合せを考えると、

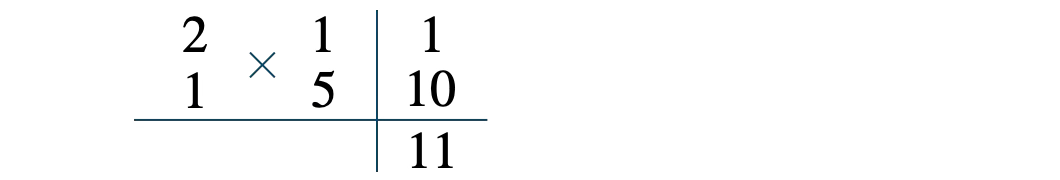
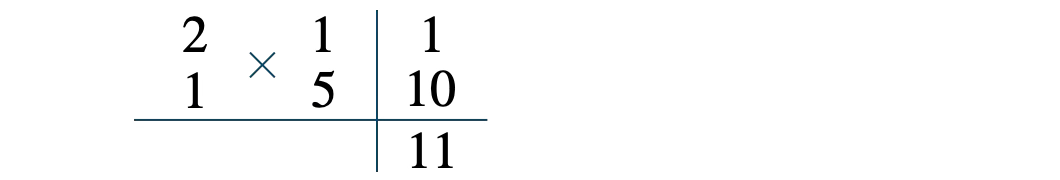
\(x\) を補って、

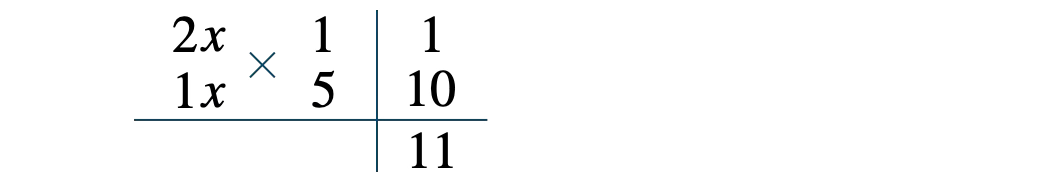
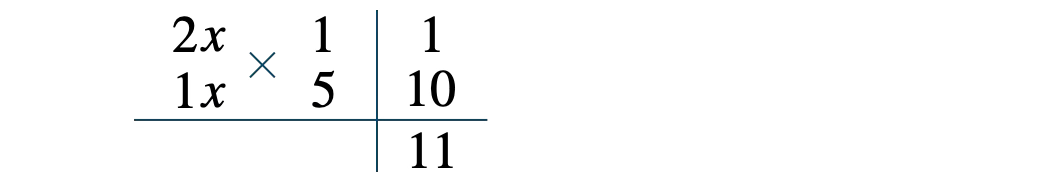
因数が \(2x+1\) と \(x+5\) となるので、

\(\begin{split}&2x^2+11x+5
\\[2pt]~~=~&(2x+1)(x+5)
\end{split}\)

よって、答えは \( (2x+1)(x+5) \)

問題次の式を因数分解せよ。

\({\small (2)}~3x^2-5x-2\)

掛けて \(3\)、掛けて \(-2\) となり、たすき掛けの和が \(-5\) となる４つの数の組合せを考えると、

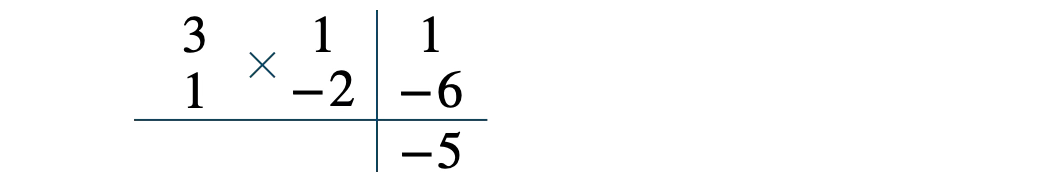
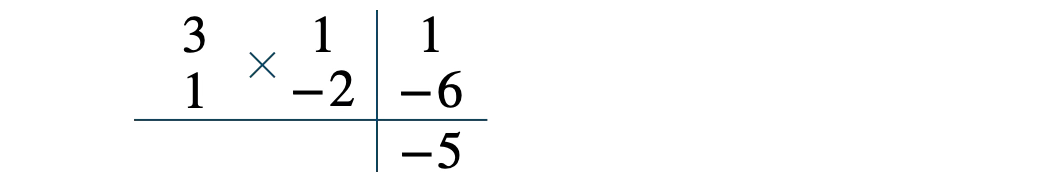
\(x\) を補って、

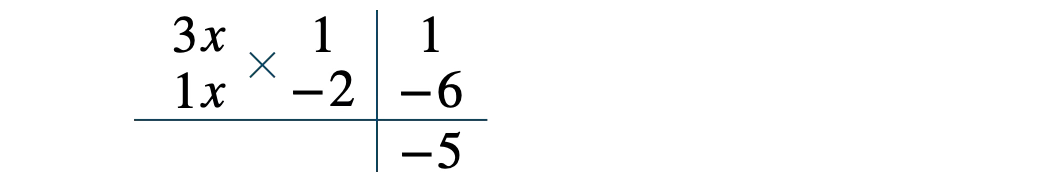
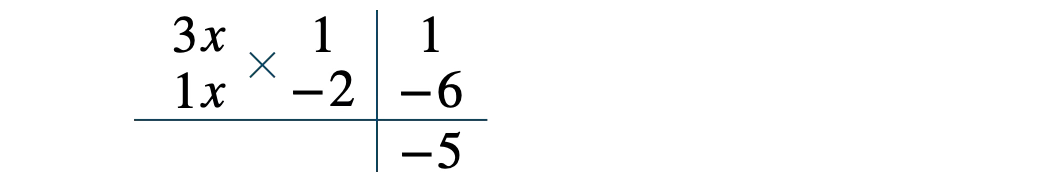
因数が \(3x+1\) と \(x-2\) となるので、

\(\begin{split}&3x^2-5x-2
\\[2pt]~~=~&(3x+1)(x-2)
\end{split}\)

よって、答えは \( (3x+1)(x-2) \)

問題次の式を因数分解せよ。

\({\small (3)}~5a^2+3ab-14b^2\)

掛けて \(5\)、掛けて \(-14\) となり、たすき掛けの和が \(3\) となる４つの数の組合せを考えると、

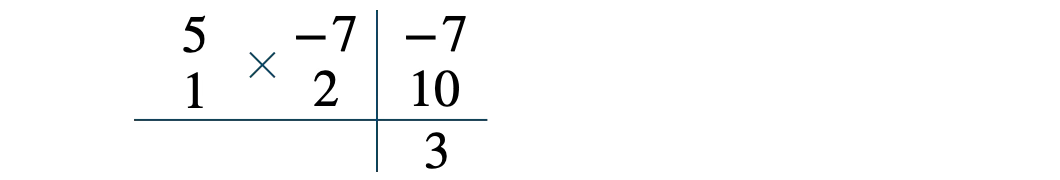
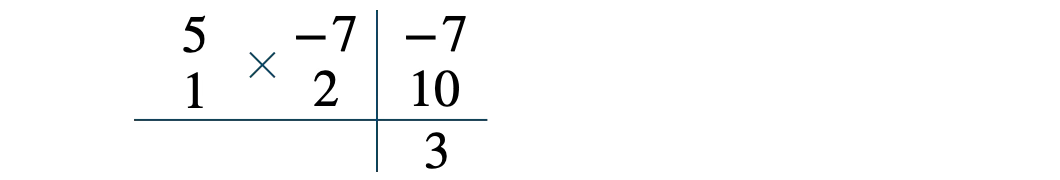
\(a\) と \(b\) を補って、

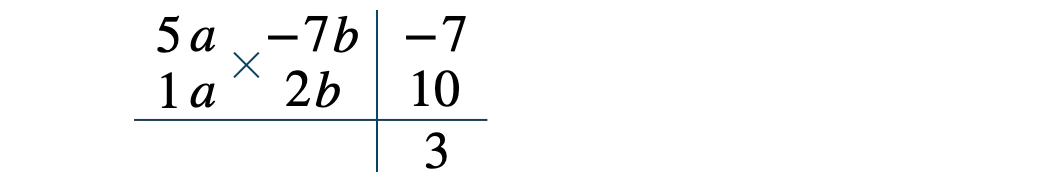
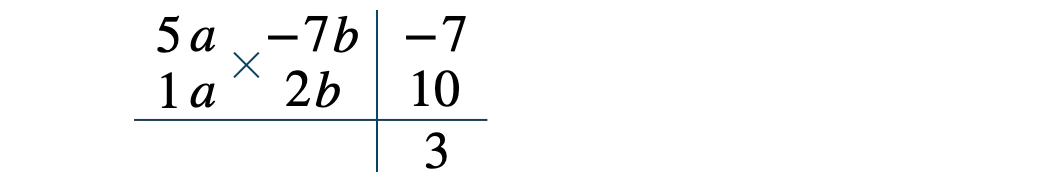
因数が \(5a-7b\) と \(a+2b\) となるので、

\(\begin{split}&3x^2-5x-2
\\[2pt]~~=~&(3x+1)(x-2)
\end{split}\)

よって、答えは \( (5a-7b)(a+2b) \)

たすき掛けを用いる因数分解の問題演習はこちらから↓