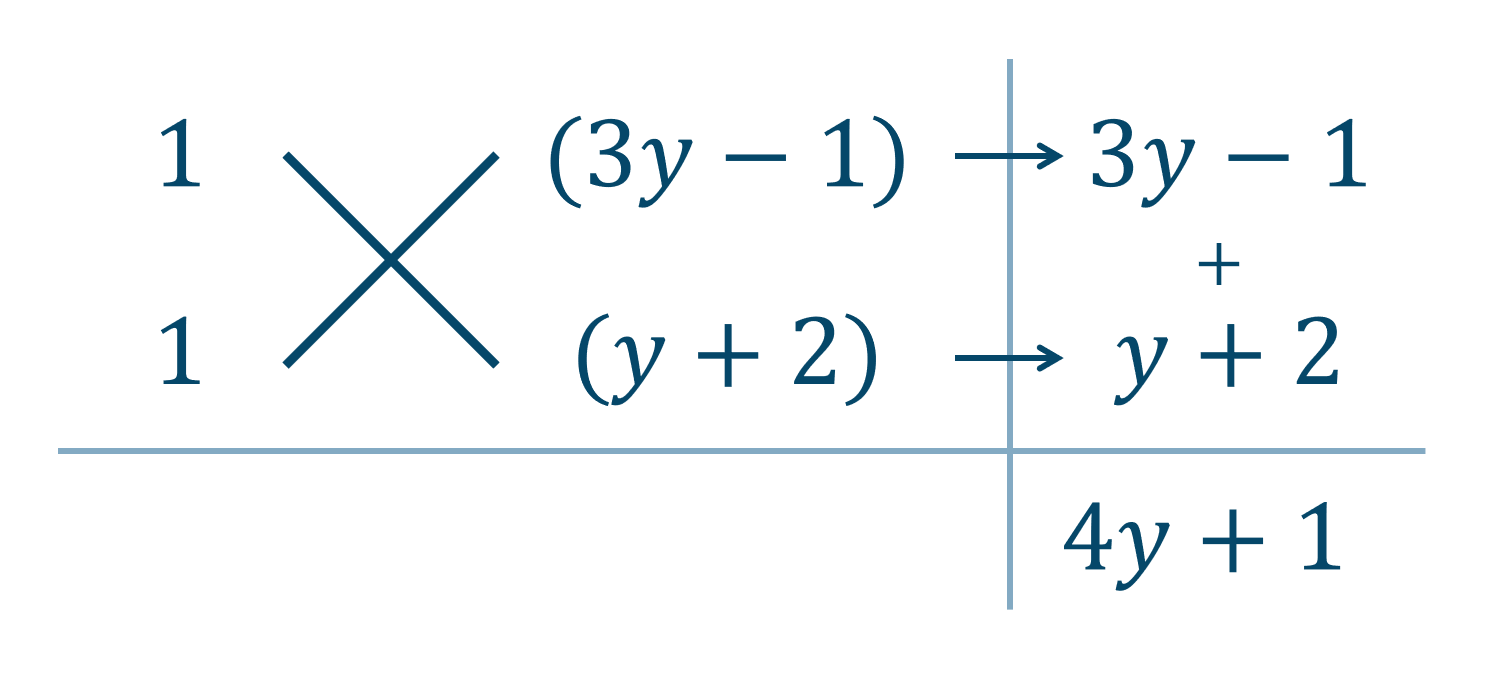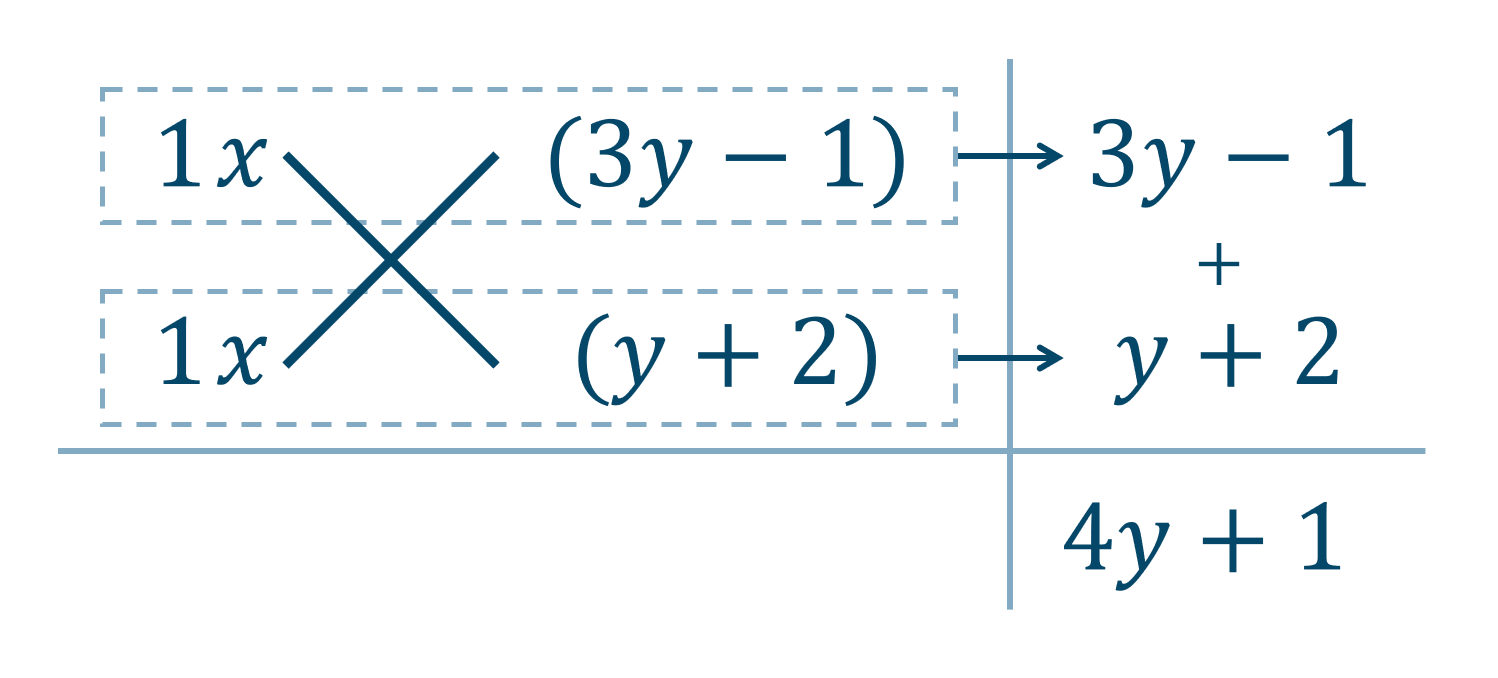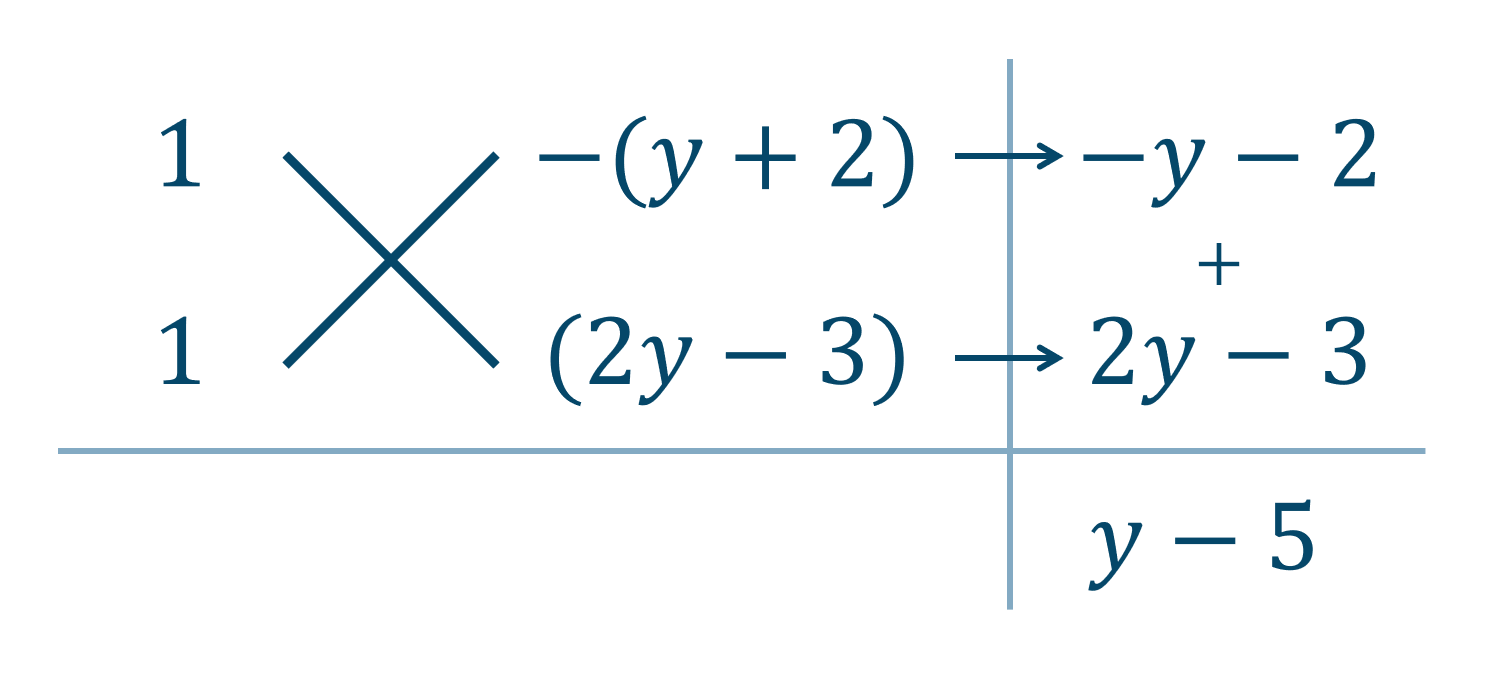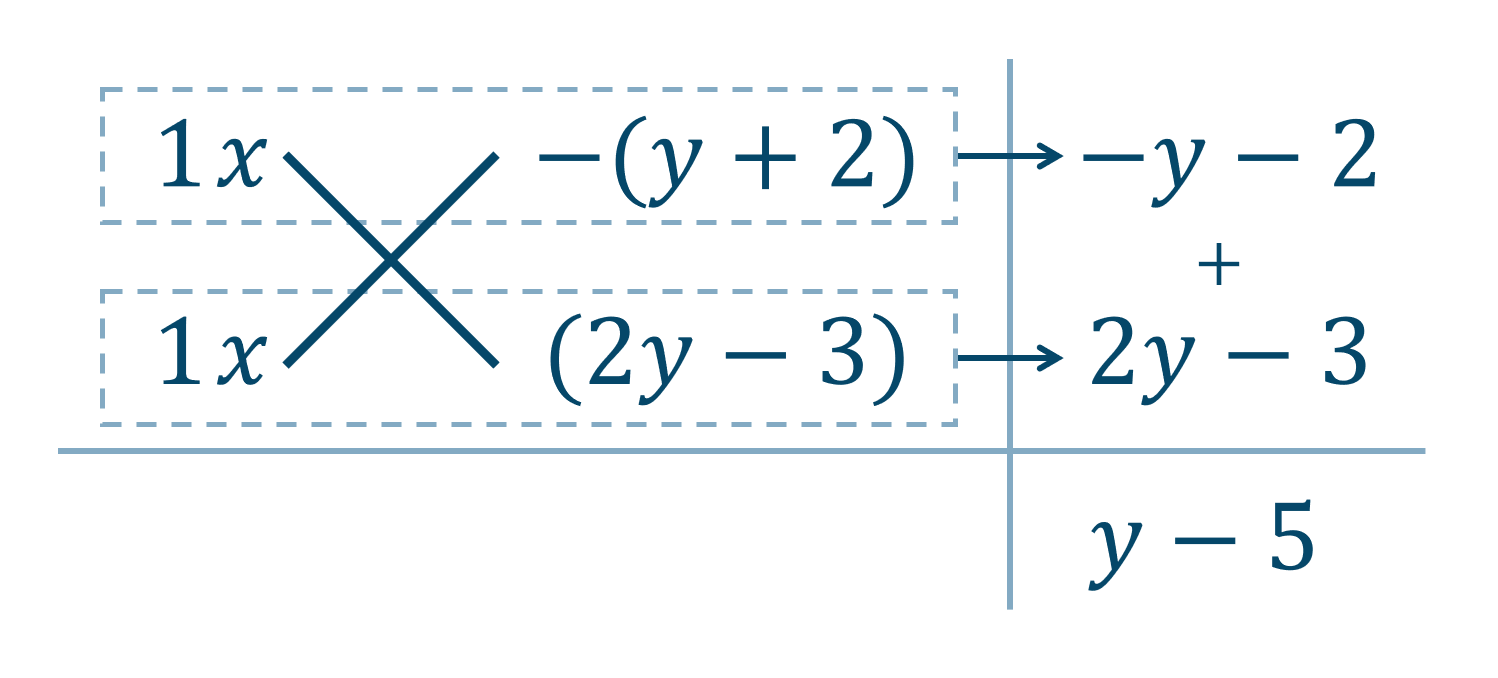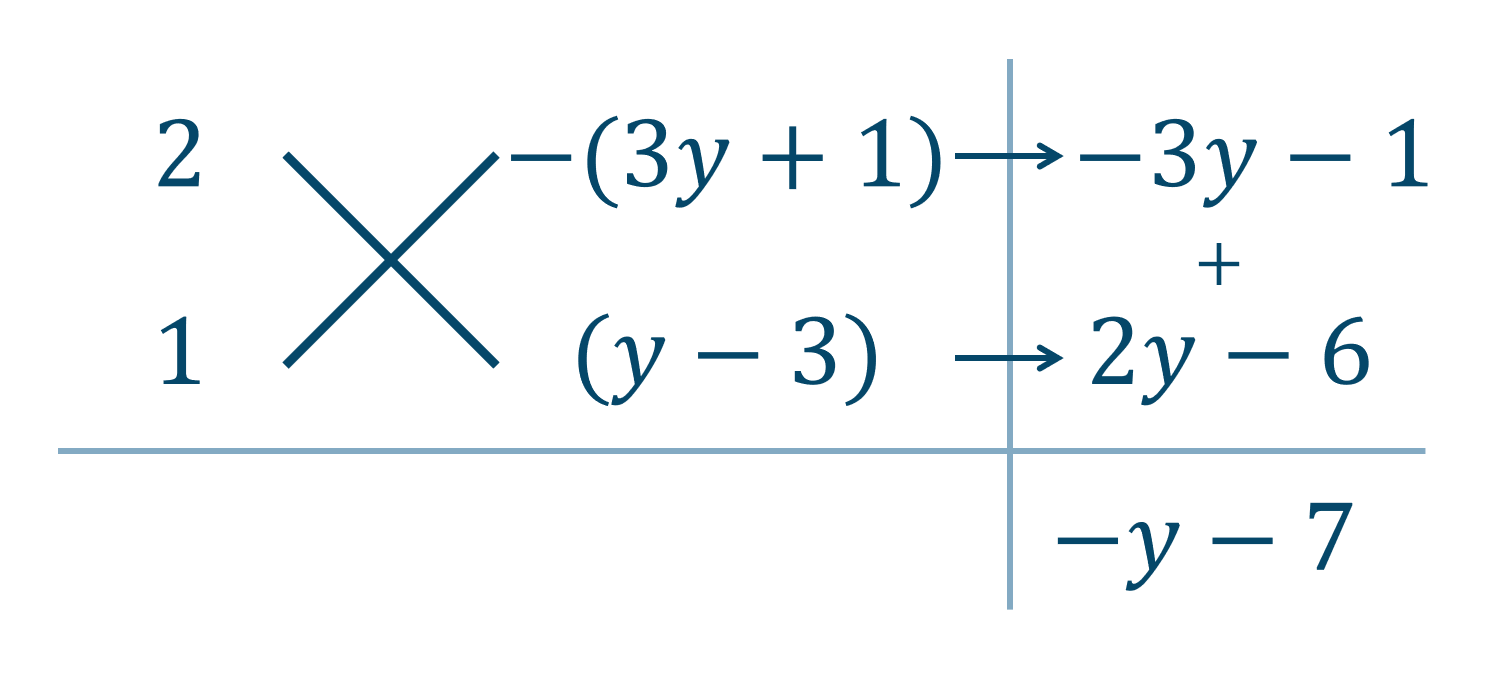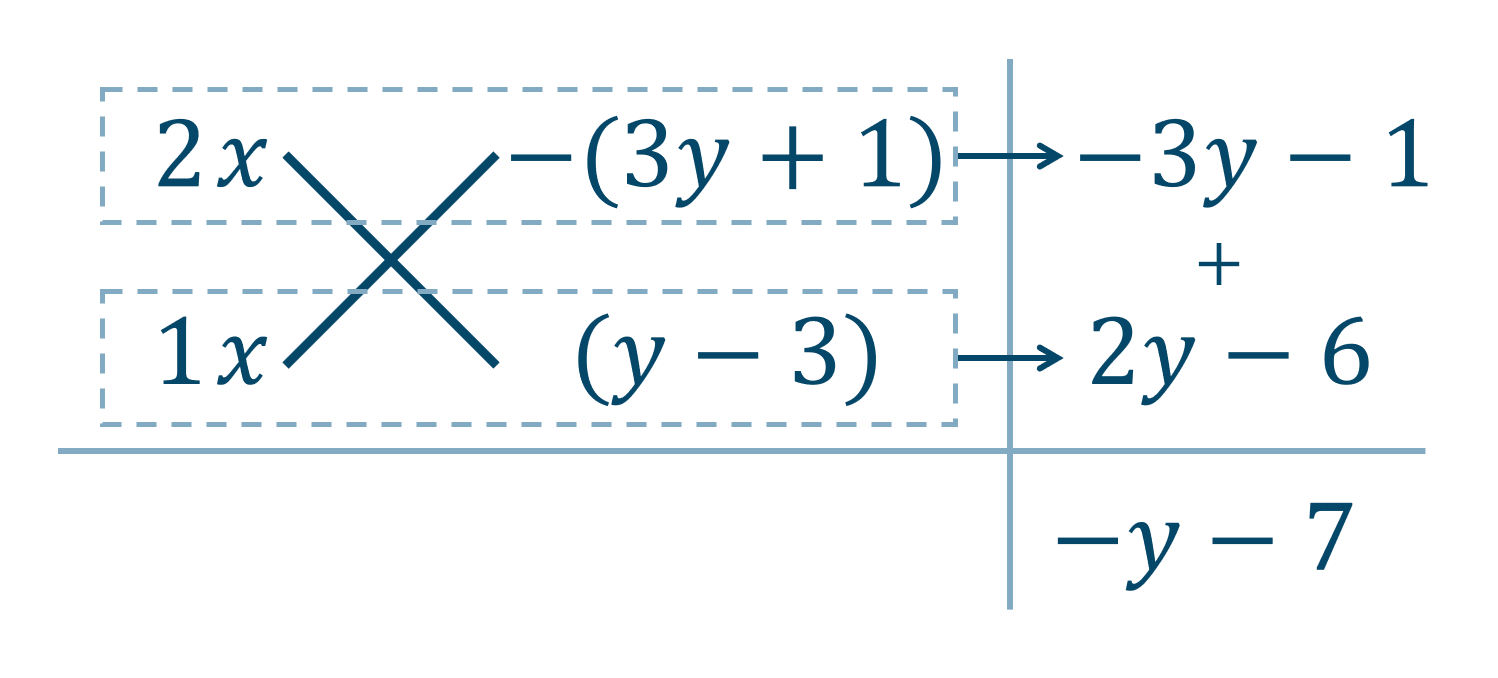文字式のたすき掛けの解法
\(~~~2x^2+(5y+5)x+(2y+3)(y-1)\)
① 数値のときと同様に組合せを考える。
掛けて \(2\)、掛けて \((2y+3)(y-1)\)、
たすき掛けの和が \((5y+5)\) となる
数と式の組合せを考えて、

② これに \(x\) を付けた式が因数となる。
\(\begin{split}=~&\left\{ 2x+(y-1) \right\}\left\{ x+(2y+3) \right\}\\[2pt]~~=~&(2x+y-1)(x+2y+3)\end{split}\)
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
問題解説:文字式のたすき掛け
問題解説(1)
\( x^2 \) の係数が \( 1 \) で、定数項が \( (3y-1)(y+2) \) であることより、次のたすき掛けの表を作成すると、
\( 4y+1 \) が \( x \) の係数となっているので、\( x \) を補って
よって、$$~~~~~~x^2+(4y+1)x+(3y-1)(y+2)$$$$~~=\{x+(3y-1)\}\{x+(y+2)\}$$$$~~=(x+3y-1)(x+y+2)$$答えは \( (x+3y-1)(x+y+2) \) となります。
問題解説(2)
\( x^2 \) の係数が \( 1 \) で、定数項が \( -(y+2)(2y-3) \) であることより、次のたすき掛けの表を作成すると、
\( y-5 \) が \( x \) の係数となっているので、\( x \) を補って
よって、$$~~~~~~x^2+(y-5)x-(y+2)(2y-3)$$$$~~=\{x-(y+2)\}\{x+(2y-3)\}$$$$~~=(x-y-2)(x+2y-3)$$答えは \( (x-y-2)(x+2y-3) \) となります。
問題解説(3)
\( x^2 \) の係数が \( 2 \) で、定数項が \( -(3y+1)(y-3) \) であることより、次のたすき掛けの表を作成すると、
\( -y-7=-(y+7) \) が \( x \) の係数となっているので、\( x \) を補って
よって、$$~~~~~~2x^2-(y+7)x-(3y+1)(y-3)$$$$~~=\{2x-(3y+1)\}\{x+(y-3)\}$$$$~~=(2x-3y-1)(x+y-3)$$答えは \( (2x-3y-1)(x+y-3) \) となります。
今回のまとめ
文字式が入っていてもたすき掛けを用いる因数分解の解法は変わりません。2種類以上の文字を含む式の因数分解でもこの計算は使うでの、ここでしできるようになりましょう。