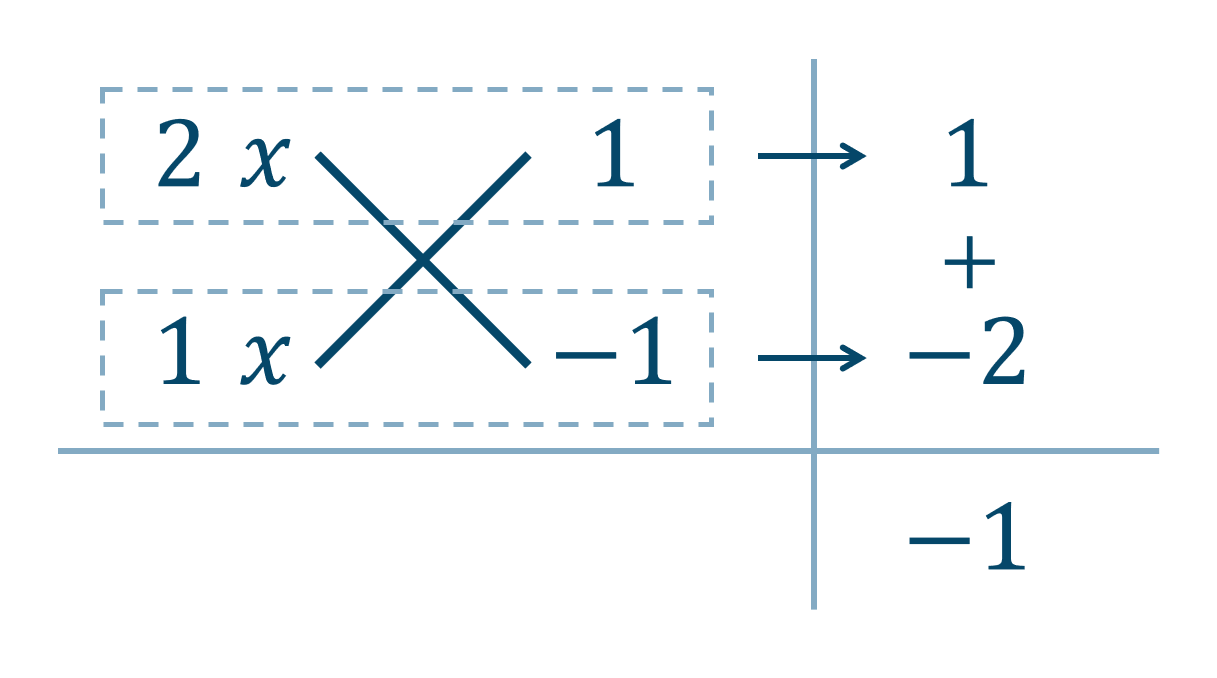2種類以上の文字を含む式の因数分解
\(~~~x^2+xy-y-1\)
① 次数の低い文字について整理する。
\(x\) に着目→2次式、\(y\) に着目→1次式
よって、\(y\) について整理すると、
\(\begin{split}&x^2+xy-y-1\\[2pt]=~&(x-1)y+x^2-1\end{split}\)
② 後半部分を部分的に因数分解する。
\(~=(x-1)y+(x+1)(x-1)\)
③ 全体的に因数分解し、( ) の中をさらに整理。
\((x-1)\) が共通因数となるので、
\(\begin{split}=~&(x-1)\left\{ y+(x+1) \right\}\\[2pt]=~&(x-1)(x+y+1)\end{split}\)
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
問題解説:2種類以上の文字を含む式の因数分解①(1次式)
問題解説(1)
\(x\) と \(y\) のどちらに着目しても1次式となります。
\(x\) について着目し解いてみましょう。$$~~~~~~xy+x-y-1$$$$~=(y+1)x-y-1$$後半部分の\(-y-1\)を部分的に因数分解すると、$$~=(y+1)x-(y+1)$$全体的に因数分解すると、\((y+1)\) を共通因数としてくくりだせるので、$$~=(y+1)(x-1)$$\(x\) → \(y\) の順番になるように並び替えると、$$~=(x-1)(y+1)$$よって、答えは \((x-1)(y+1)\) となります。
【別解】
\(y\) について着目し解いてみましょう。$$~~~~~~xy+x-y-1$$$$~=(x-1)y+x-1$$$$~=(x-1)y+(x-1)$$全体的に因数分解すると、\((x-1)\) を共通因数としてくくりだせるので、$$~=(x-1)y+(x-1)\cdot 1$$$$~=(x-1)(y+1)$$よって、答えは \((x-1)(y+1)\) となります。
問題解説(2)
\(x\) について着目すると2次式、\(y\) について着目すると1次式となるので、次数の低い \(y\) について着目し整理すると、$$~~~~~~2x^2+2xy-x+y-1$$$$~=2xy+y+2x^2-x-1$$$$~=(2x+1)y+2x^2-x-1$$後半部分の \(2x^2-x-1\) を部分的に因数分解すると、たすき掛けの表より
$$~=(2x+1)y+(2x+1)(x-1)$$全体的に因数分解すると、\((2x+1)\) を共通因数としてくくりだせるので、$$~=(2x+1)\{y+(x-1)\}$$$$~=(2x+1)(y+x-1)$$$$=(2x+1)(x+y-1)$$よって、答えは \((2x+1)(x+y-1)\) となります。
今回のまとめ
2種類以上の文字を含む式の因数分解を解説しました。公式やたすき掛けを使うだけでは因数分解できない問題もあるので、因数分解の解法の手順は必ず覚えましょう!