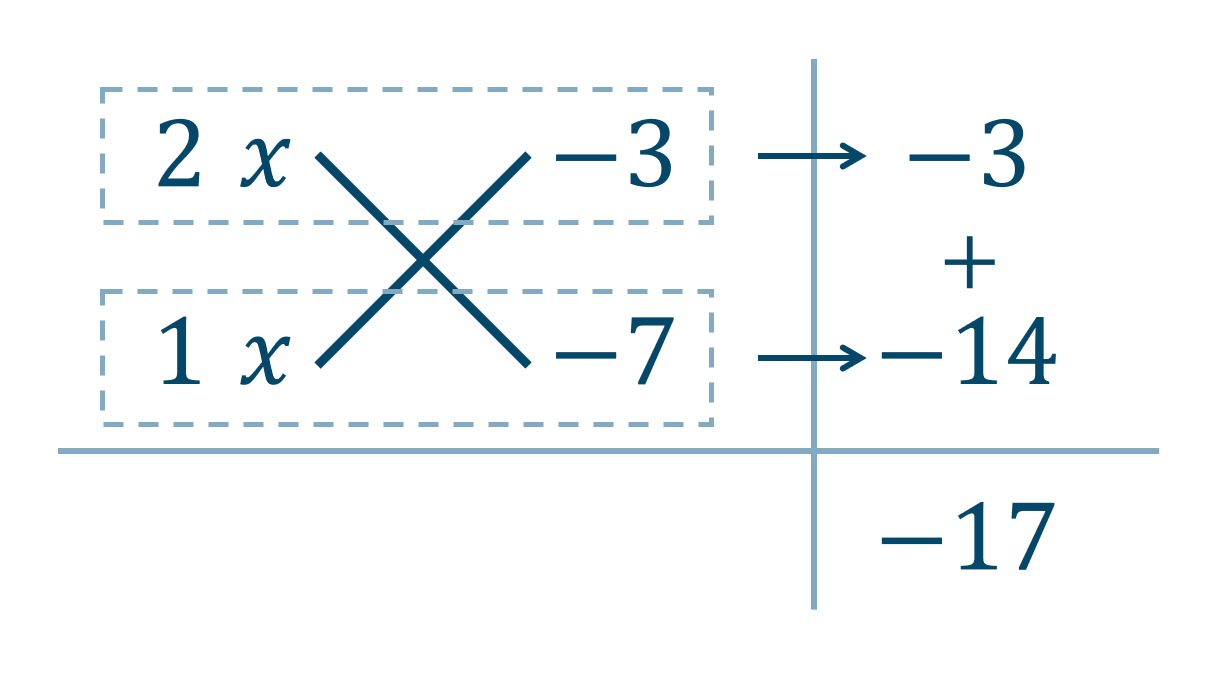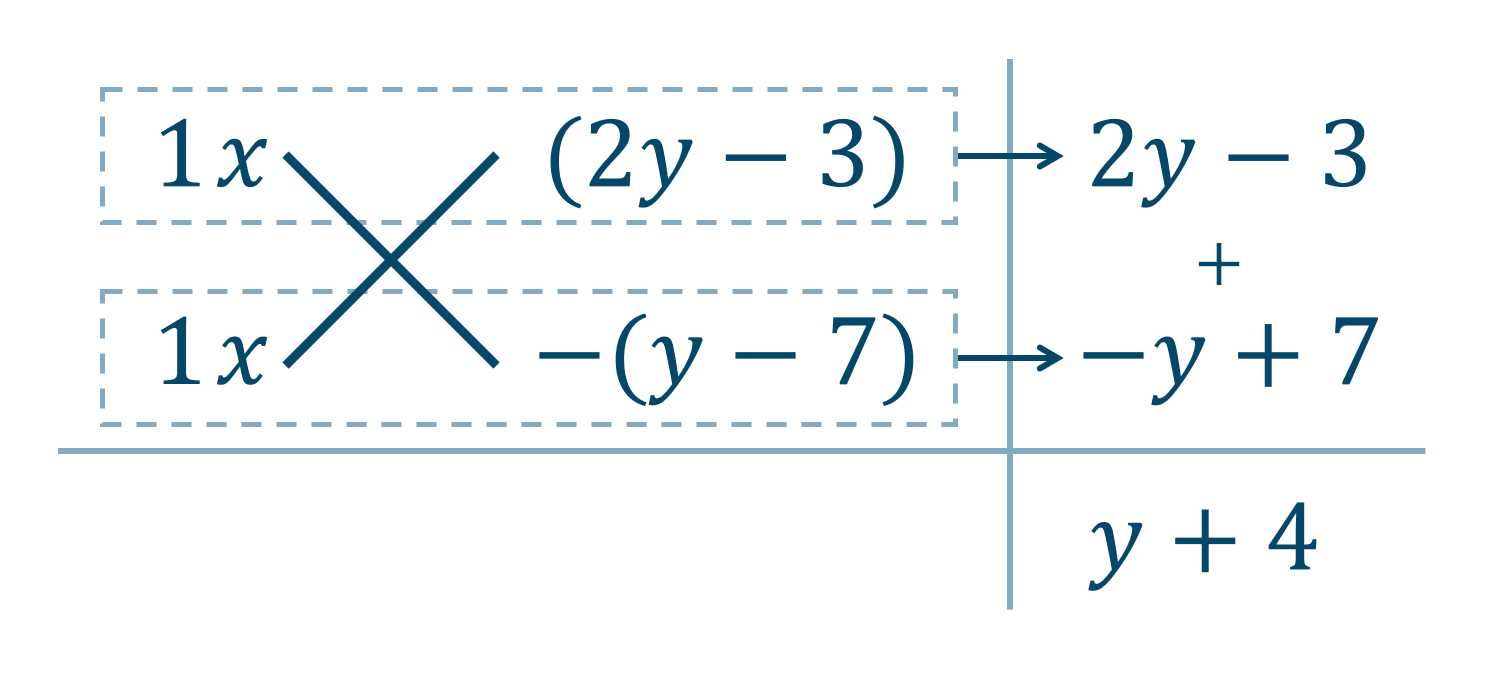2種類以上の文字を含む式の因数分解
\(~~~x^2+3xy+2y^2+3x+5y+2\)
① 1つの文字について着目して整理する。
\(x\) について整理すると、
\(~=x^2+(3y+3)x+2y^2+5y+2\)
② 部分的に因数分解をする。
後半部分を \(y\) の2次式と考えて因数分解
\(~=x^2+(3y+3)x+(2y+1)(y+2)\)
③ 全体的に因数分解をする。
掛けて \(1\)、掛けて \((2y+1)(y+2)\)
たすき掛けの和が \((3y+3)\) となる
数と式の組合せを考えて、

④ これに \(x\) を付けた式が因数となり、( )の中をさらに整理する。
\(\begin{split}~~=~&\left\{x+(2y+1) \right\}\left\{x+(y+2) \right\}\\[2pt]~~=~&(x+2y+1)(x+y+2)\end{split}\)
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
3種類の文字を含む2次式の因数分解の方法は、
\(\small~~~a^2b+ab^2+b^2c+bc^2+c^2a+ca^2+2abc\)
① 1つの文字について着目して整理する。
\(a\) について着目して整理すると、
\(\small~=(b+c)a^2+(b^2+2bc+c^2)a+b^2c+bc^2\)
② 部分的に因数分解をする。
\((b^2+2bc+c^2)\) と \((b^2c+bc^2)\) を
それぞれ部分的に因数分解すると、
\(~=(b+c)a^2+(b+c)^2a+bc(b+c)\)
③ 全体的に因数分解をする。
\((b+c)\) が共通因数となるので、
\(~=(b+c)\left\{ a^2+(b+c)a+bc \right\}\)
④ さらに( )の中を因数分解する。
\(\left\{a^2+(b+c)a+bc\right\}\) を因数分解すると、
\(~=(b+c)(a+b)(a+c)\)
⑤ 答えるときは、\(a\to b\to c\to a\to \cdots\) の順になるように並べかえる。
\(\begin{split}~~=~&(a+b)(b+c)(a+c)\\[2pt]~~=~&(a+b)(b+c)(c+a)\end{split}\)
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
問題解説:2種類以上の文字を含む式の因数分解②(2次式)
問題解説(1)
\(x\) と \(y\) のどちらに着目しても2次式となります。
\(x\) について着目し解いてみましょう。$$~~~~~~x^2+xy-2y^2+4x+17y-21$$$$~=x^2+xy+4x-2y^2+17y-21$$$$~=x^2+(y+4)x-2y^2+17y-21$$ここで、後半部分の \(-2y^2+17y-21\) を \(-1\) でくくると、$$~=x^2+(y+4)x-(2y^2-17y+21)$$よって、\(2y^2-17y+21\) を部分的な因数分解すると、たすき掛けの表より
$$~=x^2+(y+4)x-(2y-3)(y-7)$$次に全体的な因数分解すると、文字式のたすき掛けの表より
$$~= \{ x+(2y-3) \} \{ x-(y-7)\} $$$$~=(x+2y-3)(x-y+7)$$よって、答えは \((x+2y-3)(x-y+7) \) となります。
問題解説(2)
\(a\) と \(b\) と \(c\) のどれに着目しても2次式となります。
\(a\) について着目し解いてみましょう。$$~~~~~~a^2b+ab^2+b^2c+bc^2+c^2a+ca^2+2abc$$$$~=a^2b+ca^2+ab^2+c^2a+2abc+b^2c+bc^2$$$$~=(b+c)a^2+(b^2+c^2+2bc)a+b^2c+bc^2$$ここで、部分的な因数分解すると、$$~b^2+c^2+2bc=b^2+2bc+c^2=(b+c)^2$$また、\( b^2c+bc^2=bc(b+c)\) よって、$$~=(b+c)a^2+(b+c)^2a+bc(b+c)$$ここで、全体的な因数分解すると、\( (b+c)\) でくくりだせるので$$~=(b+c) \{ a^2+(b+c)a+bc \}$$次に\(\{~~\}\)の中を因数分解すると、$$~=(b+c)(a+b)(a+c)$$\(a\) → \(b\) → \(c\) → \(a\) → …の順に並べ替えて、 $$~=(a+b)(b+c)(c+a)$$よって、答えは \((a+b)(b+c)(c+a) \) となります。
今回のまとめ
前回と今回で2種類以上の文字を含む式の因数分解を解説しました。解法の手順が複雑ですが、④1つの文字に着目→⑤部分的な因数分解→⑥全体的な因数分解の流れは必ず覚えてできるようになりましょう!