連立不等式の解法
① それぞれの1次不等式の解を求める。
② その解の範囲を数直線上に表す。
③ 2つの範囲の共通範囲が解となる。
例えば、\(x≧-1\) かつ \(x<3\) では、

共通範囲より、解は \(-1≦x<3\) となる
また、\(x≧-1\) かつ \(x>3\) では、

共通範囲より、解は \(x>3\)となる
■ \(A<B<C\) の連立不等式
\(\begin{split}\biggl\{ \begin{eqnarray} A<B \\ B<C \end{eqnarray} \end{split}\)
このように、2つの1次不等式に分けて、連立不等式として計算できる。
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
問題解説:連立不等式の解
問題解説(1)
$$~~~\biggl\{ ~~\begin{eqnarray} 2x-3<x+5 ~~~\cdots ① \\ 3x-9≦0~~~ \cdots ②\end{eqnarray} $$①の不等式について、$$~~~2x-3<x+5$$\(-3\) を右辺に、\(x\) を左辺に移項すると、$$~~~2x-x<5+3$$$$\hspace{32pt}x<8$$よって、\(x<8\) となります。
②の不等式について、$$~~~~~3x-9≦0$$\(-9\) を右辺に移項すると、$$\hspace{28pt}3x≦9$$両辺を \(3\) でわり算すると、不等号の向きはそのままなので、$$\hspace{35pt}x≦3$$よって、\(x≦3\) となります。
したがって、それぞれの解の範囲より、
答えは、\(x≦3\) となります。
問題解説(2)
この連立不等式は
$$~~~\biggl\{~~ \begin{eqnarray} -x+3≦3x+1~~\cdots ① \\ 3x+1<x+7~~\cdots ②\end{eqnarray} $$として求めることができます。
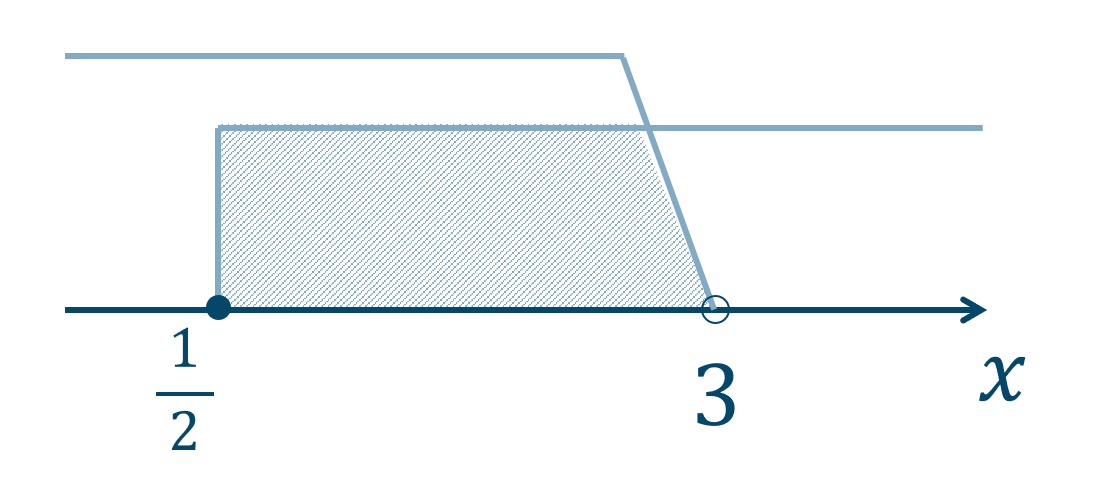
①の不等式について、$$~~~-x+3≦3x+1$$\(3\) を右辺に、\(3x\) を左辺に移項すると、$$\hspace{7pt}-x-3x≦1-3$$$$\hspace{25pt}-4x≦-2$$\(-4\) で両辺をわり算すると、不等号の向きが逆になるので、$$\hspace{37pt}x≧\frac{1}{2}$$よって、\(x≧\Large{\frac{1}{2}}\) となります。
②の不等式について、$$~~~3x+1<x+7$$\(1\) を右辺に、\(x\) を左辺に移項すると、$$\hspace{5pt}3x-x<7-1$$$$\hspace{23pt}2x<6$$\(2\) で両辺をわり算すると、不等号の向きはそのままなので、$$\hspace{31pt}x<3$$よって、\(x<3\) となります。
したがって、それぞれの解の範囲より、
答えは、\({\Large\frac{1}{2}}≦x<3\) となります。
今回のまとめ
連立不等式は範囲を数直線上に表し、その共通範囲より解を求めることになります。共通範囲の読み取りに注意しましょう!