不等式を満たす整数の解
① 与えられた不等式の解を求める。
② 解の範囲を数直線上に表す。
③ 範囲を満たす整数解を目で見て読み取る。
例えば、\(1< x≦{\Large \frac{\,7\,}{\,2\,}}\)を満たす整数解すべては、
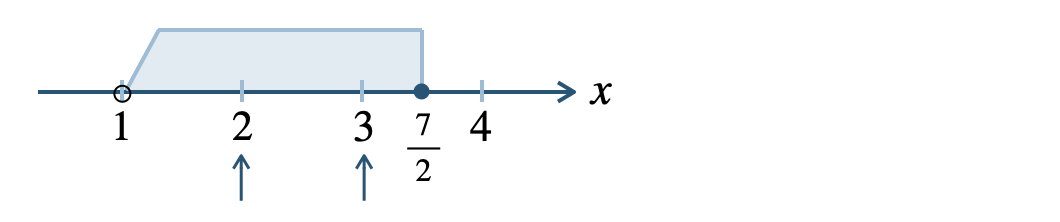
数直線より、答えは \(x=2~,~3\) となる
※ \(x=1\) は含まない
また、\(x<{\Large \frac{\,8\,}{\,3\,}}\) を満たす最大の整数は、
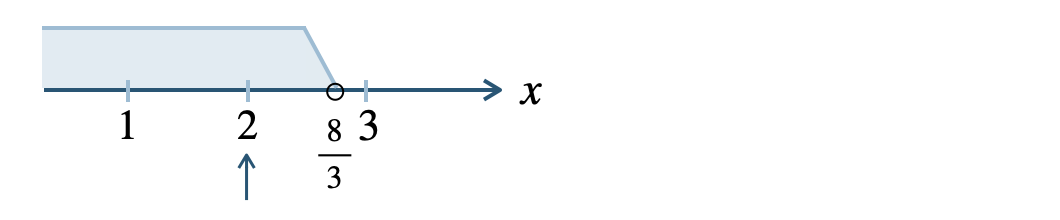
数直線より、答えは \(x=2\) となる
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
問題解説:不等式を満たす整数の解
問題解説(1)
\({\small (1)}~\)次の不等式を満たす最小の整数 \(x\) を求めよ。$$~~~12(x-3)>2x+9$$
1次不等式を解くと、$$~~~12(x-3)>2x+9$$$$\hspace{12pt}12x-36>2x+9$$\(-36\) を右辺に、\(2x\) を左辺に移項すると、$$\hspace{12pt}12x-2x>9+36$$$$\hspace{33pt}10x>45$$\(10\) で両辺をわり算すると、不等号の向きはそのままなので、$$\hspace{41pt}x>\frac{45}{10}=4.5$$よって、数直線上に表すと、
数直線上の範囲より、この不等式を満たす最小の整数は \(5\) となります。
よって、答えは \(x=5\) となります。
問題解説(2)
\({\small (2)}~\)次の不等式を満たす最大の整数 \(x\) を求めよ。$$~~~\frac{x+1}{5}>\frac{x+3}{2}$$
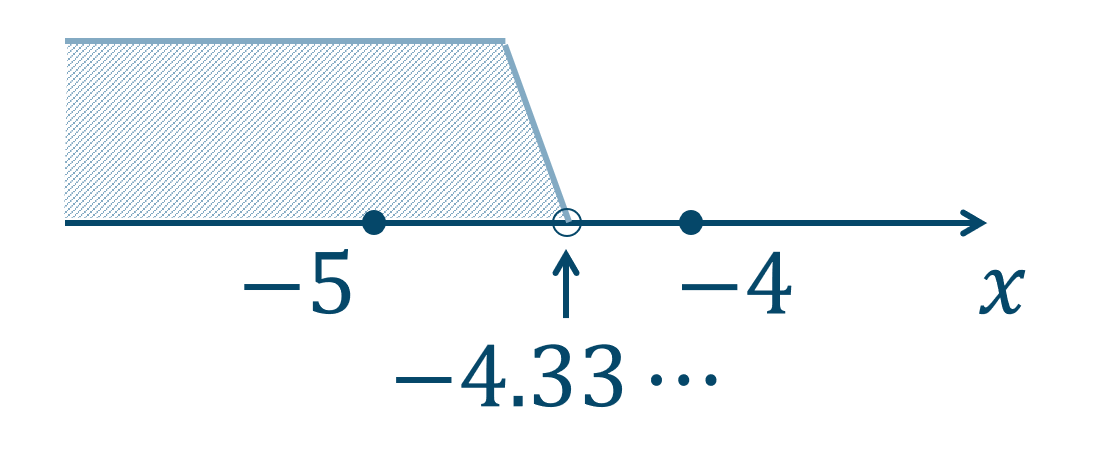
1次不等式を解くと、$$\hspace{25pt}\frac{x+1}{5}>\frac{x+3}{2}$$両辺に \(10\) をかけ算すると、不等号の向きはそのままなので、$$~~\frac{x+1}{5}\times 10>\frac{x+3}{2}\times 10$$$$\hspace{5pt}(x+1)\times 2>(x+3)\times 5$$$$\hspace{24pt}2x+2>5x+15$$\(2\) を右辺に、\(5x\) を左辺に移項すると、$$\hspace{15pt}2x-5x>15-2$$$$\hspace{30pt}-3x>13$$\(-3\) で両辺をわり算すると、不等号の向きが逆になるので、$$\hspace{40pt}x<-\frac{13}{3}=-4.33\cdots $$よって、数直線上に表すと、
数直線上の範囲より、この不等式を満たす最大の整数は \(-5\) となります。
よって、答えは \(x=-5\) となります。
今回のまとめ
1次不等式の整数の解を求める問題は、数直線に解の範囲を書き視覚的に問題を解けるようになりましょう!
https://yorikuwa.com/m11[blogcard url=”00/