指数関数のグラフ

2018.10.202020.06.09

問題解説：指数関数のグラフ

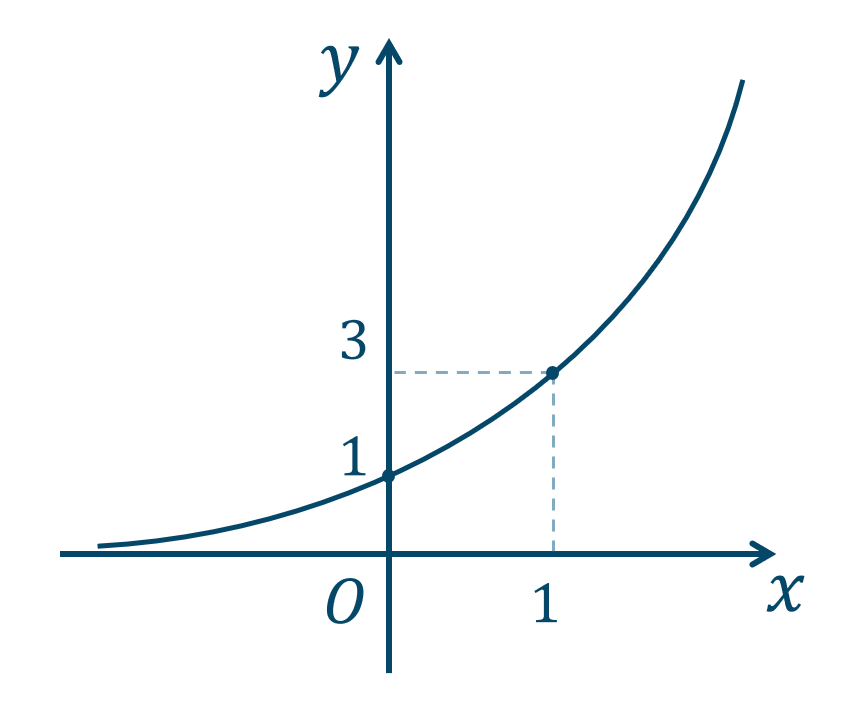
問題次の関数のグラフを描け。$${\small (1)}~y=3^x$$

底が $1<3$ であることより、$x$ が増加すると、$y$ も増加する単調増加のグラフとなります。
また、$y>0$ となり、$x$ 軸が漸近線となります。
また、点 $(0~,~1)$ を通ります。
したがって、グラフの概形は、

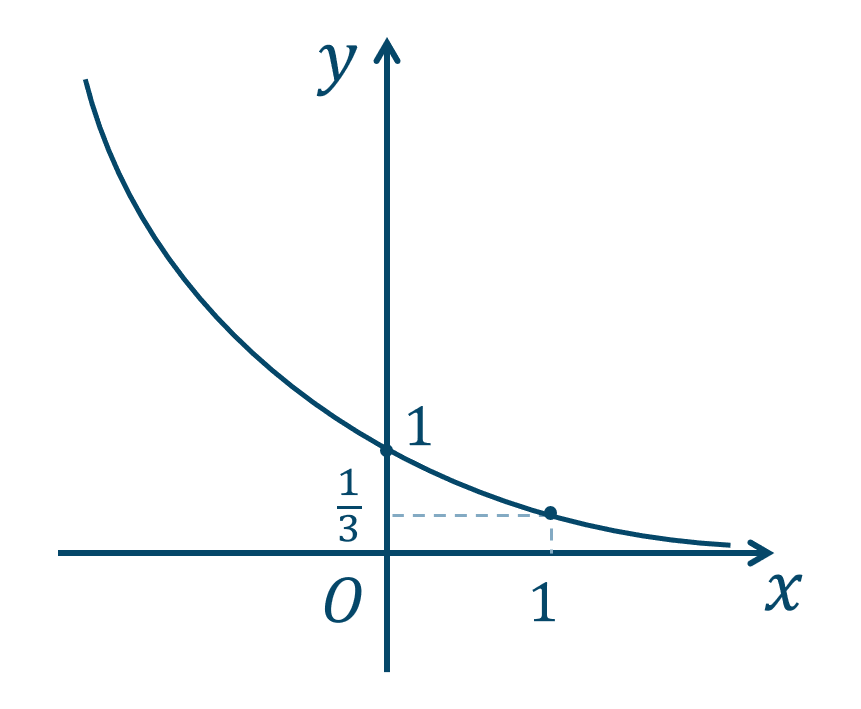
問題次の関数のグラフを描け。$${\small (2)}~y=\left( \frac{1}{3} \right)^x$$

底が $0<{\large \frac{1}{3}}<1$ であることより、$x$ が増加すると、$y$ は減少する単調減少のグラフとなります。
また、$y>0$ となり、$x$ 軸が漸近線となります。
また、点 $(0~,~1)$ を通ります。
したがって、グラフの概形は、

指数関数のグラフは底の値によってグラフの概形がかわるので、今回の問題の２つのパターンを覚えておきましょう。