問題解説:円形に並べる確率
問題解説(1)
\({\small (1)}~\)特定の2人が隣り合う
すべての場合の数は、6人を円形に並べることより、
よって、\((6-1)!=5!\) 通りとなります。
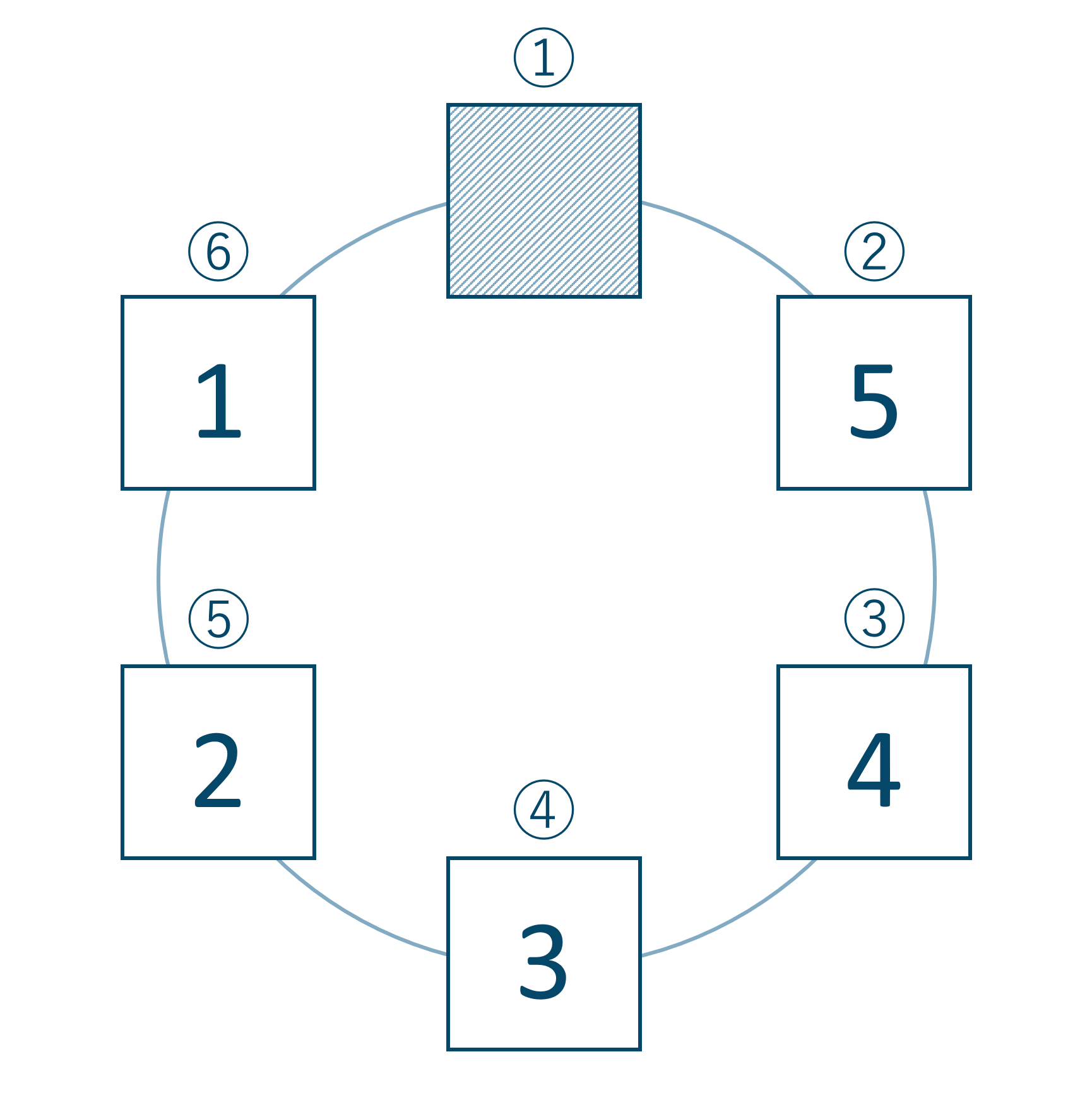
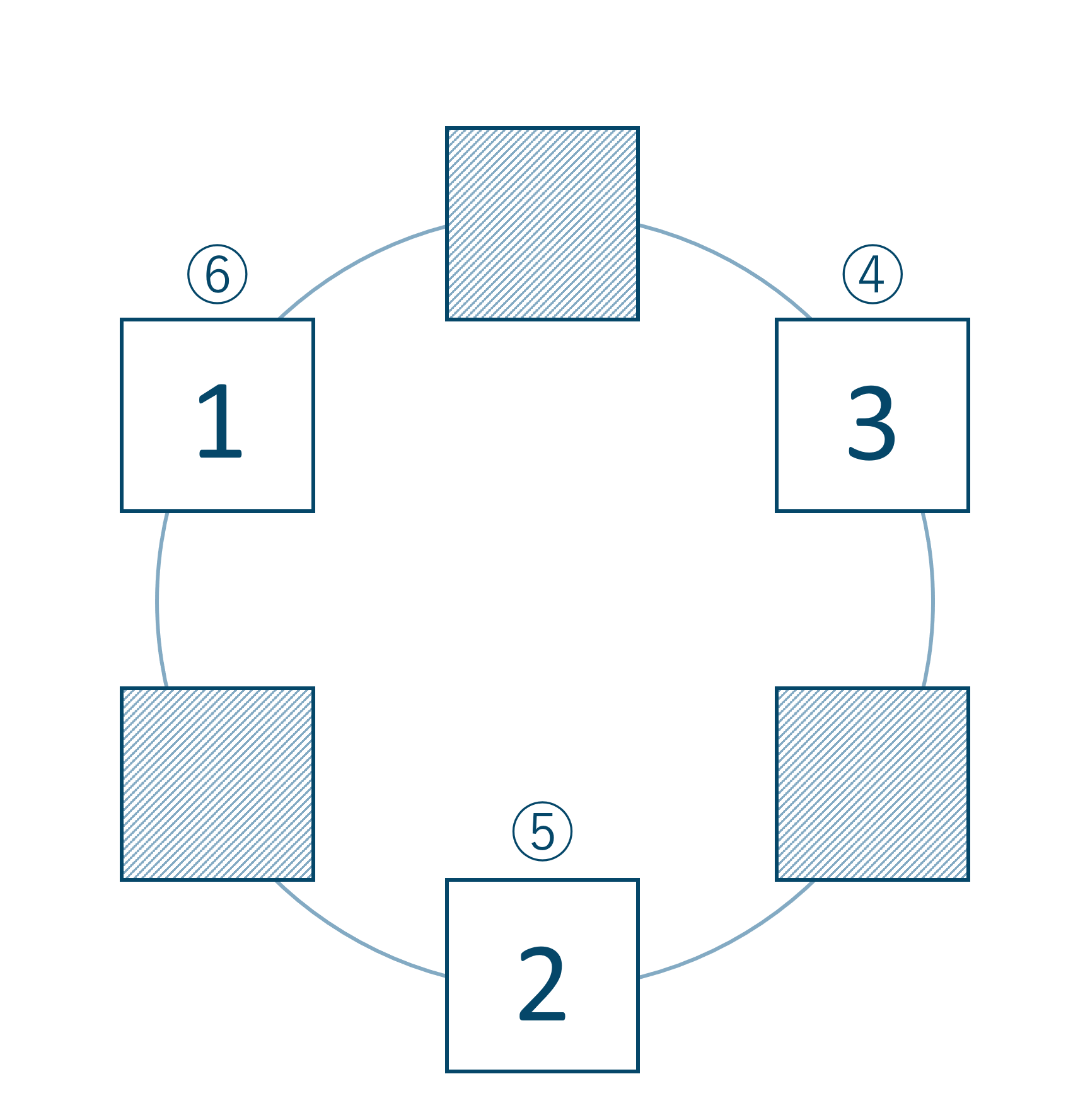
次に特定の2人が隣り合うときは次の図のようになる
よって、特定の2人を固定させて残りの4人を並べ場合の数は \(4!\) 通り。
また、隣り合う2人の並び方は \(2!\) 通り。
「連続して起こる」ので積の法則より、\(4! \times 2!\) 通りとなります。
したがって、求める確率は$$~~~~~~\frac{4! \times 2!}{5!}$$$$~=\frac{4 \times 3 \times 2 \times 1 \times 2 \times1}{5 \times 4 \times 3 \times 2 \times1}$$$$~=\frac{2}{5}$$答えは \( {\Large \frac{2}{5}} \) となります。
問題解説(2)
\({\small (2)}~\)特定の2人が向い合う
すべての場合の数は(1)と同様に \(5!\) 通りとなります。
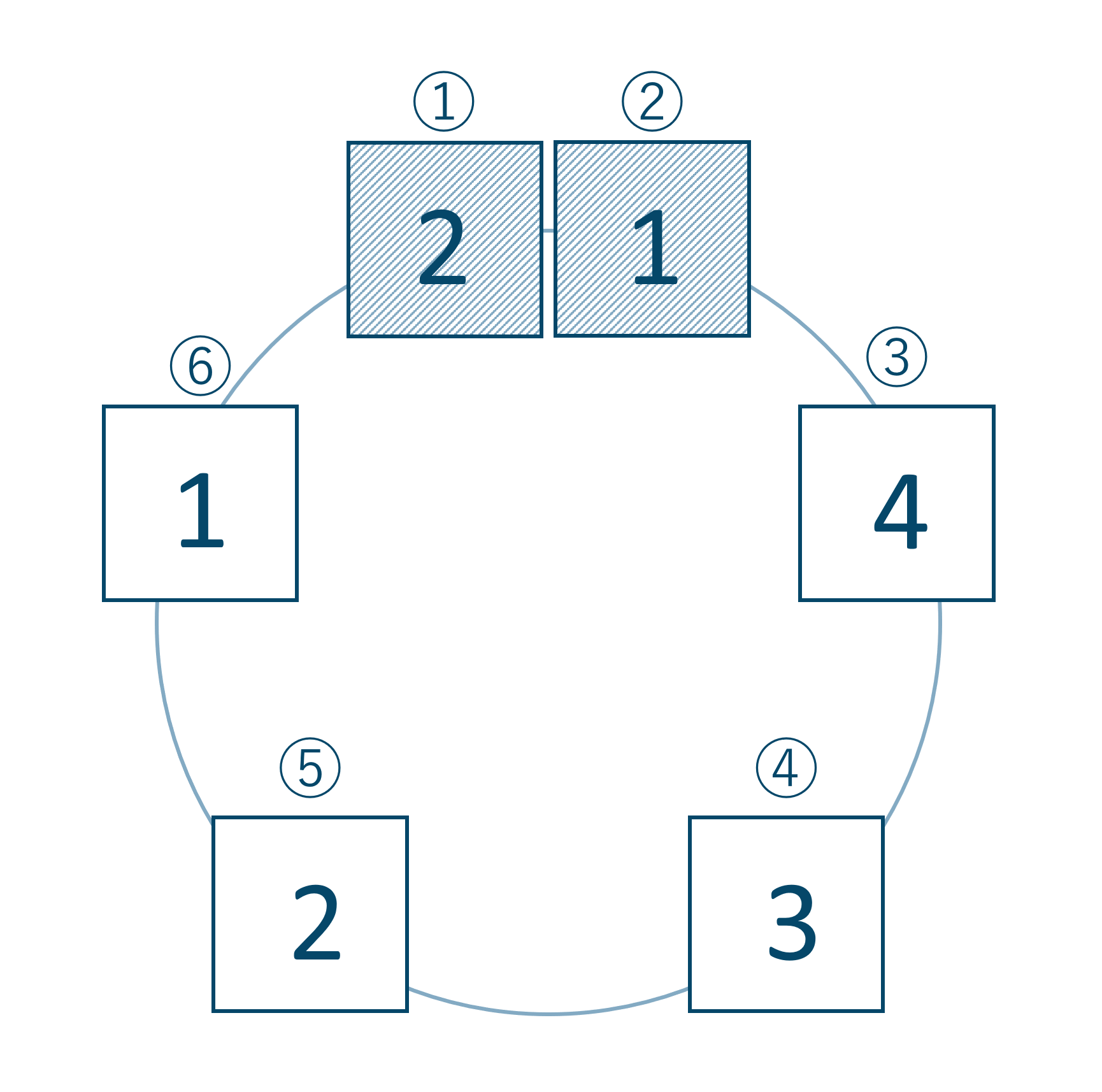
特定の2人が向い合うのは、この2人を向い合せで固定しましょう。
このとき、回転するとダブってしまうので2人の入れ替わりは考えなくてよくなります。
残りの4人を順に並べていくので、その並べ方は \(4!\) となります。
したがって求める確率は、$$~~~~~~\frac{4!}{5!}$$$$~=\frac{4 \times 3 \times 2 \times 1}{5 \times 4 \times 3 \times 2 \times1}$$$$~=\frac{1}{5}$$答えは \( {\Large \frac{1}{5}} \) となります。
問題解説(3)
\({\small (3)}~\)男女が交互に座る
すべての場合の数は(1)、(2)と同様に円順列として考えて \(5!\) となります。
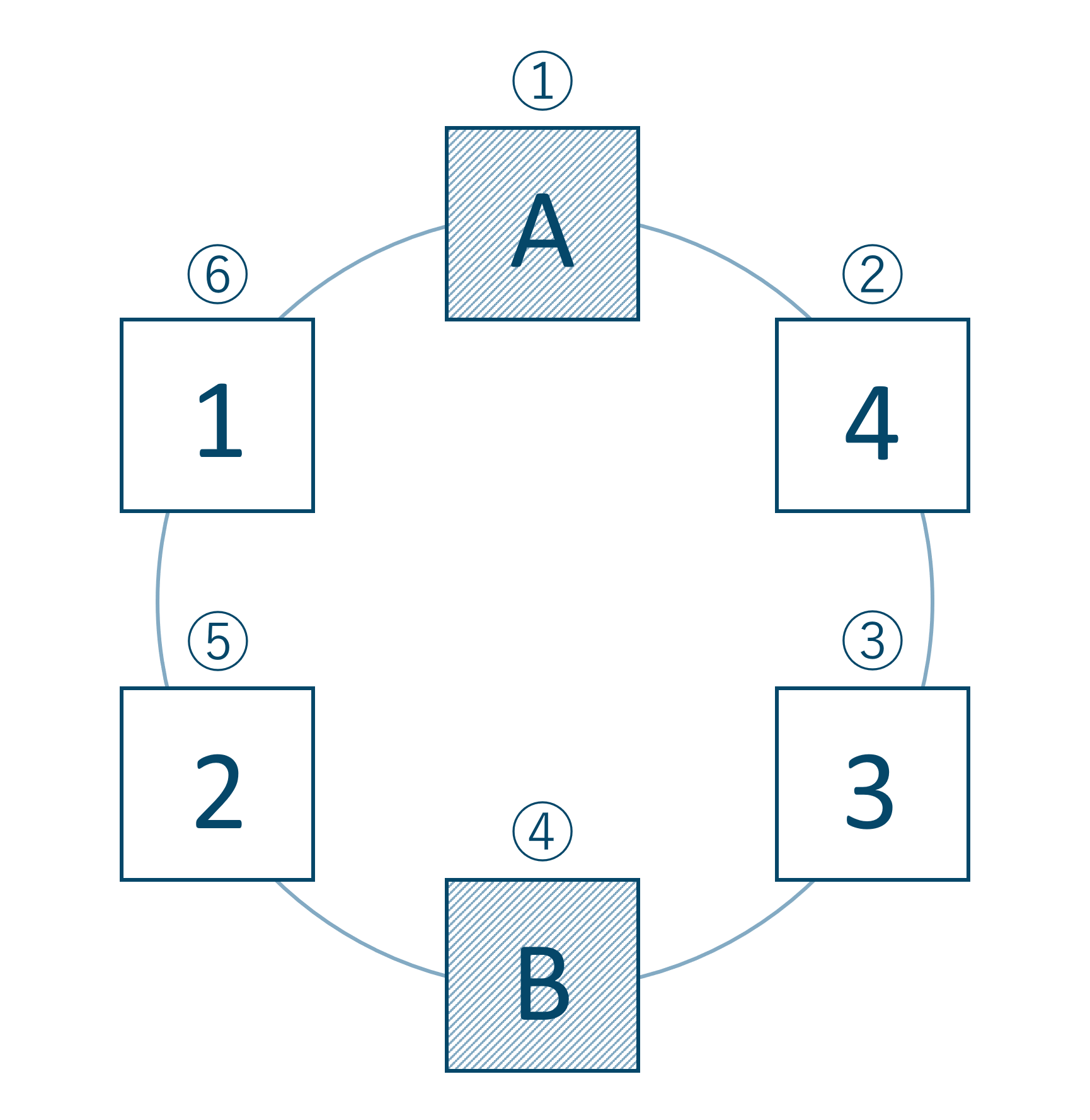
男女が交互に並ぶときは、まずは男子3人を円形に並べましょう。
図より円順列となるので、\((3-1)!=2!\) 通りとなります。
次にこの男子3人の位置が固定されたと考えて、残りの女子を次の図の3カ所に並べます。
よって、\(3!\) 通りとなります。
これらは「連続して起こる」ので積の法則より、\(2!\times 3!\) 通りとなります。
したがって求める確率は、$$~~~~~~\frac{2!\times 3!}{5!}$$$$~=\frac{2 \times1\times 3 \times 2 \times 1}{5 \times 4 \times 3 \times 2 \times1}$$$$~=\frac{2}{5\times4}$$$$~=\frac{1}{10}$$答えは \( {\Large \frac{1}{10}} \) となります。
今回のまとめ
円順列の求め方は「固定させる!」でしたが条件が付くことによって解法が変わります。それぞれのパターンをしっかりと理解しておきましょう。また、階乗の計算は確率の式を作ったあとに約分を利用して解きましょう!