楕円の標準形

2020.09.292020.10.04

楕円の標準形の解法
問題解説：楕円の標準形
1. 問題解説(1)
2. 問題解説(2)
今回のまとめ

楕円の標準形の解法

Point：楕円の標準形２つの焦点からの距離の和が一定（＝長軸の長さ）である点の軌跡を楕円という。
標準形は次のようになる。

$$\frac{\,x^2 \,}{\,a^2 \,}+\frac{\,y^2 \,}{\,b^2 \,}=1$$

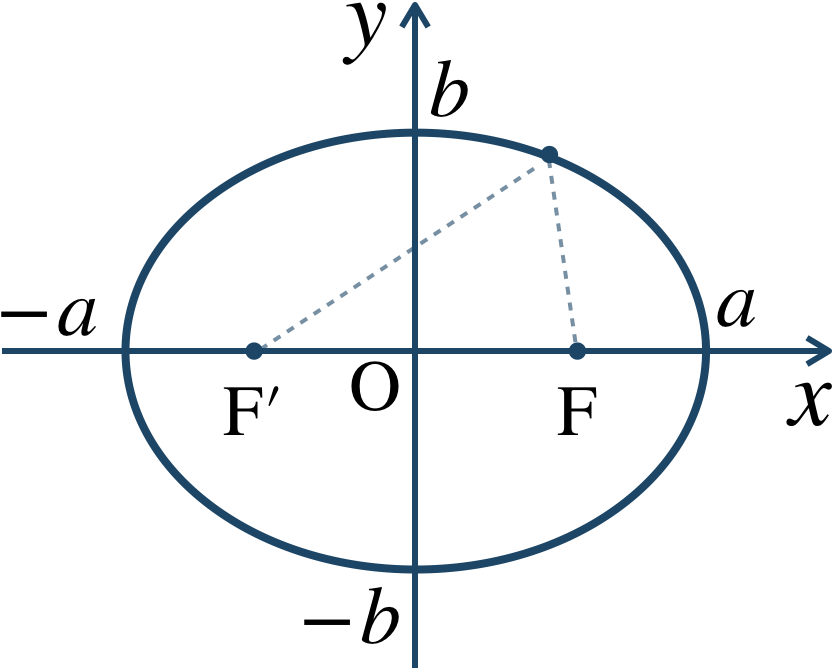
(1) $a\gt b\gt0$ のとき
$x$ 軸上に焦点があり、$$~~~c=\sqrt{a^2-b^2}$$とすると、焦点は、$$~~~{\rm F}(c~,~0)~,~{\rm F}'(-c~,~0)$$となる。
中心は原点 $(0~,~0)$ で、長軸の長さ $2a$ で短軸の長さ $2b$ となる。
また、楕円上の任意の点から２つの焦点までの距離の和が $2a$ で一定となる。
概形は、

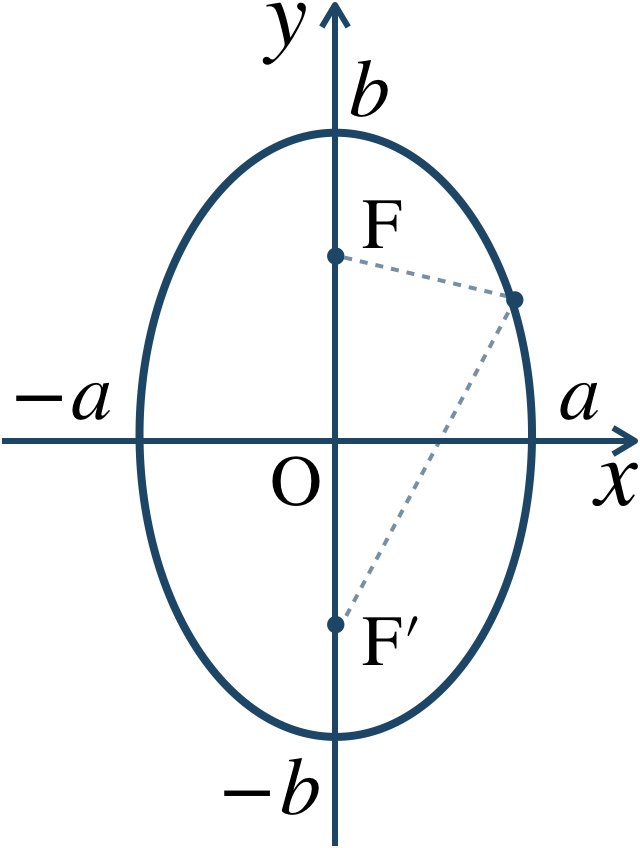
(2) $b\gt a\gt0$ のとき
$y$ 軸上に焦点があり、$$~~~c=\sqrt{b^2-a^2}$$とすると、焦点は、$$~~~{\rm F}(0~,~c)~,~{\rm F}'(0~,~-c)$$となる。
中心は原点 $(0~,~0)$ で、長軸の長さ $2b$ で短軸の長さ $2a$ となる。
また、楕円上の任意の点から２つの焦点までの距離の和が $2b$ で一定となる。
概形は、

問題解説：楕円の標準形

問題解説(1)

問題次の問いに答えよ。
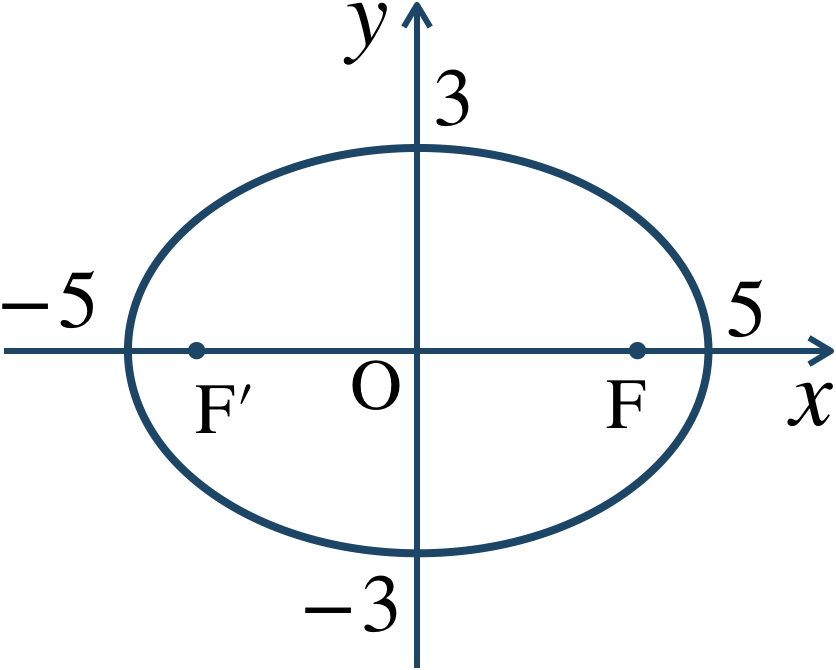
${\small (1)}~$次の楕円の長軸と短軸の長さ、焦点の座標を求めて、概形をかけ。$$~{\large ①}~\frac{\,x^2 \,}{\,25 \,}+\frac{\,y^2 \,}{\,9 \,}=1$$$$~{\large ②}~9x^2+4y^2=36$$

$${\large ①}~~~\frac{\,x^2 \,}{\,5^2 \,}+\frac{\,y^2 \,}{\,3^2 \,}=1$$これより、$a=5~,~b=3$ となる。
$a\gt b$ より、$x$ 軸上に焦点がある楕円となり、長軸の長さは、$$~~~2a=2\times5=10$$短軸の長さは、$$~~~2b=2\times3=6$$また、$c=\sqrt{a^2-b^2}$ より、$$~~~c=\sqrt{5^2-3^2}$$$$~~~~\,=\sqrt{25-9}$$$$~~~~\,=\sqrt{16}=4$$よって、焦点は、$$~~~{\rm F}(4~,~0)~,~{\rm F}'(-4~,~0)$$概形は、

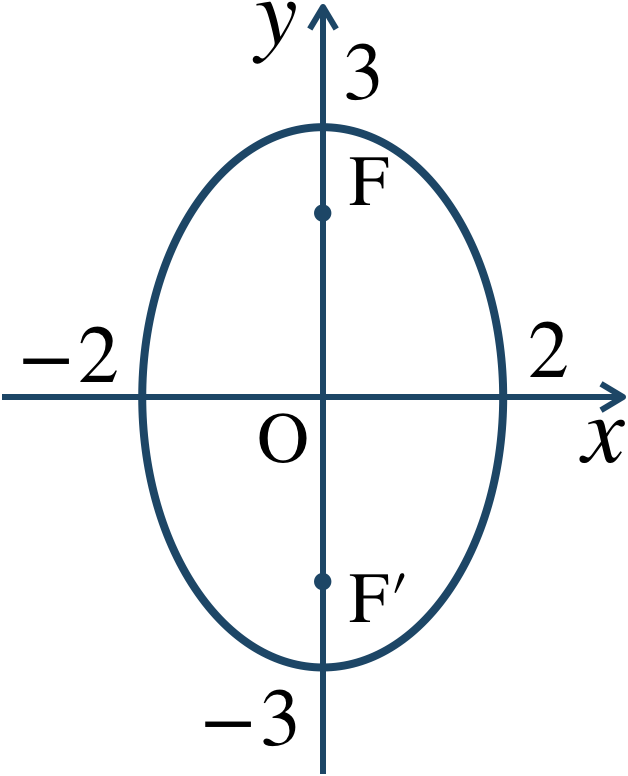
${\large ②}$ 両辺を $\div36$ すると、$$~~~\frac{\,9x^2 \,}{\,36 \,}+\frac{\,4y^2 \,}{\,36 \,}=\frac{\,36 \,}{\,36 \,}$$$$~~~~~~~\frac{\,x^2 \,}{\, 2^2\,}+\frac{\,y^2 \,}{\,3^2 \,}=1$$これより、$a=2~,~b=3$ となる。
$b\gt a$ より、$y$ 軸上に焦点がある楕円となり、長軸の長さは、$$~~~2b=2\times3=6$$短軸の長さは、$$~~~2a=2\times2=4$$また、$c=\sqrt{b^2-a^2}$ より、$$~~~c=\sqrt{3^2-2^2}$$$$~~~~\,=\sqrt{9-4}=\sqrt{5}$$よって、焦点は、$$~~~{\rm F}\left(0~,~\sqrt{5}\right)~,~{\rm F}’\left(0~,~-\sqrt{5}\right)$$概形は、

問題解説(2)

問題次の問いに答えよ。
${\small (2)}~$２点 $\left(\sqrt{7}~,~0\right)~,~\left(-\sqrt{7}~,~0\right)$ を焦点として、この２点からの距離の和が $8$ である楕円の方程式を求めよ。

焦点が $\left(\sqrt{7}~,~0\right)~,~\left(-\sqrt{7}~,~0\right)$ であるので、楕円の方程式は、$$~~~\frac{\,x^2 \,}{\,a^2 \,}+\frac{\,y^2 \,}{\,b^2 \,}=1~~~\cdots~{\large ①}$$（ただし、$a\gt b\gt 0$ ）とおける。

$c=\sqrt{a^2-b^2}$ より、$$~~~\sqrt{a^2-b^2}=\sqrt{7}$$$$~~~~~~~\,a^2-b^2=7~~~\cdots~{\large ②}~$$また、焦点からの距離の和が $8$ であるので、$$~~~2a=8$$$$~~~~\,a=4$$②に代入すると、$$~~~4^2-b^2=7$$$$~~~~~~\,-b^2=7-16$$$$~~~~~~\,-b^2=-9$$$$~~~~~~~~~~~\,b^2=9$$$b \gt 0 $ より、$$~~~b=3$$よって、$a=4~,~b=3$ を①に代入すると、$$~~~\frac{\,x^2 \,}{\,4^2 \,}+\frac{\,y^2 \,}{\,3^2 \,}=1$$したがって、$$~~~\frac{\,x^2 \,}{\,16 \,}+\frac{\,y^2 \,}{\,9 \,}=1$$となる。