複素数平面上の直線のなす角の解法
2点 \({\rm A}(\alpha)~,~{\rm B}(\beta)\) と実軸の正の向きとのなす角は、
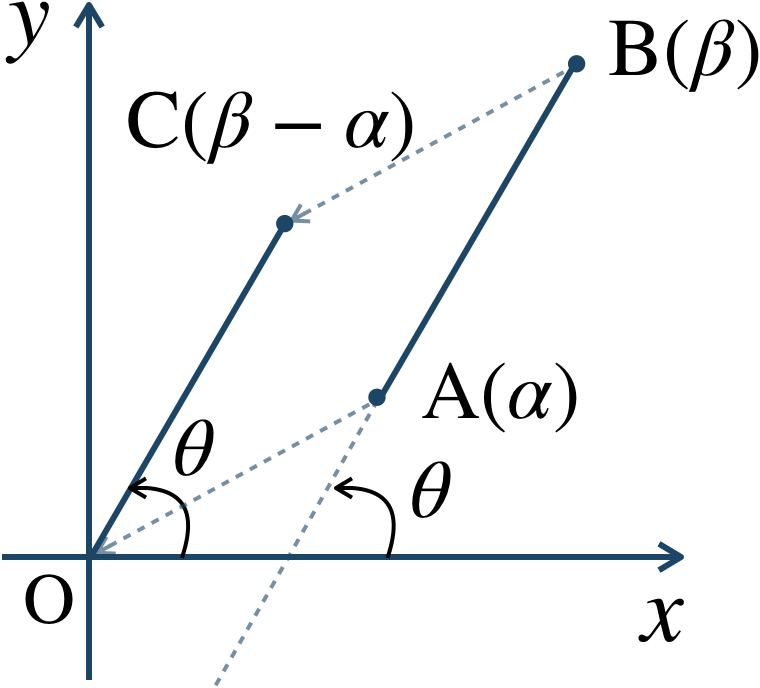
点 \({\rm A}\) を原点まで平行移動したとき、点 \({\rm B}\) が点 \({\rm C}\) に移動したと考える。
これより、直線 \({\rm OC}\) と実軸の正の向きとのなす角 \(\theta\) を求めればよいので、点 \({\rm C}\) を表す複素数 \(\beta-\alpha\) より、
したがって、複素数 \(\beta-\alpha\) の偏角 \(\theta\) となる。
■ 複素数平面上の2直線のなす角
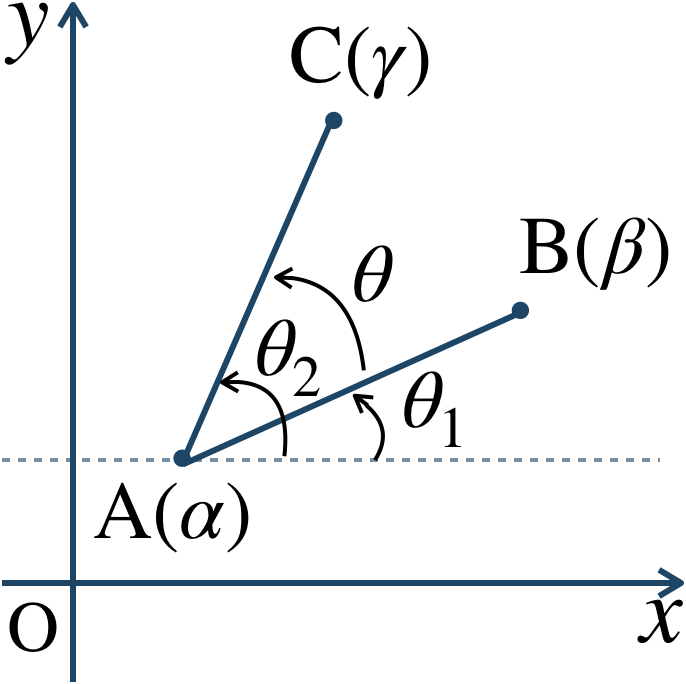
3点 \({\rm A}(\alpha)~,~{\rm B}(\beta)~,~{\rm C}(\gamma)\) について、\(\angle {\rm BAC}\) の値は、
\(\angle {\rm BAC}=\theta\) は、
直線 \({\rm AC}\) は実軸との正の向きとのなす角 \(\theta_2\)
から
直線 \({\rm AB}\) は実軸との正の向きとのなす角 \(\theta_1\)
を引けばよいの、$$~~~\theta=\theta_2-\theta_1$$また、$$~~~\theta_1=\arg (\beta-\alpha)~,~\theta_2=\arg (\gamma-\alpha)$$これより、$$~~~\theta=\arg (\gamma-\alpha)-\arg (\beta-\alpha)$$ド・モアブルの定理の逆より、計算すると、
したがって、点 \({\rm A}(\alpha)~,~{\rm B}(\beta)~,~{\rm C}(\gamma)\) について、\(\angle {\rm BAC}\) の値は、複素数 \({\large \frac{\,\gamma-\alpha\,}{\,\beta-\alpha\,}}\) の偏角 \(\theta\) となる。
問題解説:複素数平面上の直線のなす角
問題解説(1)
\({\small (1)}~\)2点 \({\rm A}\left(1-\sqrt{3}i\right)~,~{\rm B}\left(4+2\sqrt{3}i\right)\) において、直線 \({\rm AB}\) と実軸との正の向きとのなす角を求めよ。
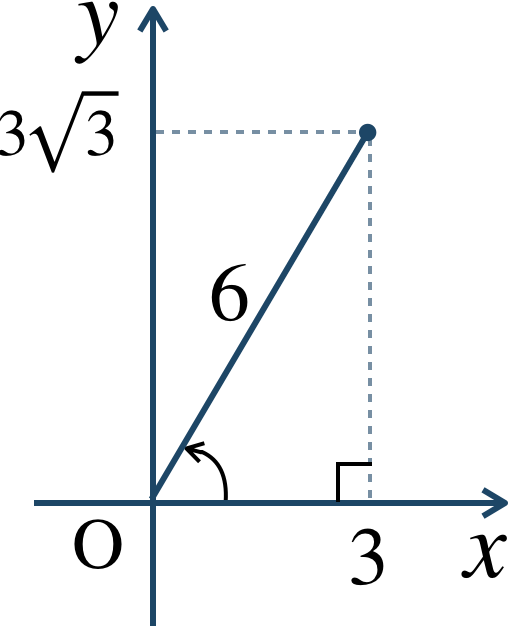
点 \({\rm A}\) を原点まで平行移動したとき、同様に点 \({\rm B}\) を平行移動した点は、$$~~~~~~\left(4+2\sqrt{3}i\right)-\left(1-\sqrt{3}i\right)$$$$~=4+2\sqrt{3}i-1+\sqrt{3}i$$$$~=3+3\sqrt{3}i$$これを極形式で表すと、絶対値は、$$~~~~~~\left|3+3\sqrt{3}i\right|$$$$~=\sqrt{3^2+(3\sqrt{3})^2}$$$$~=\sqrt{9+27}=\sqrt{36}=6$$また、複素数平面上に表すと、
これより、偏角は \({\large \frac{\,\pi\,}{\,3\,}}\) となる
よって、$$~~~6\left(\cos{\frac{\,\pi \,}{\,3 \,}}+i\sin{\frac{\,\pi \,}{\,3 \,}}\right)$$直線 \({\rm AB}\) と実軸の正の向きとのなす角を \(\theta\) をとすると、$$~~~\theta=\arg \left(3+3\sqrt{3}i\right)=\frac{\,\pi \,}{\,3 \,}$$したがって、答えは \({\large \frac{\,\pi\,}{\,3\,}}\) となる。
問題解説(2)
\({\small (2)}~\)3点 \({\rm A}(-3+2i)~,~{\rm B}(2i)~,~{\rm C}(-9+8i)\) において、\(\angle{\rm BAC}\) を求めよ。
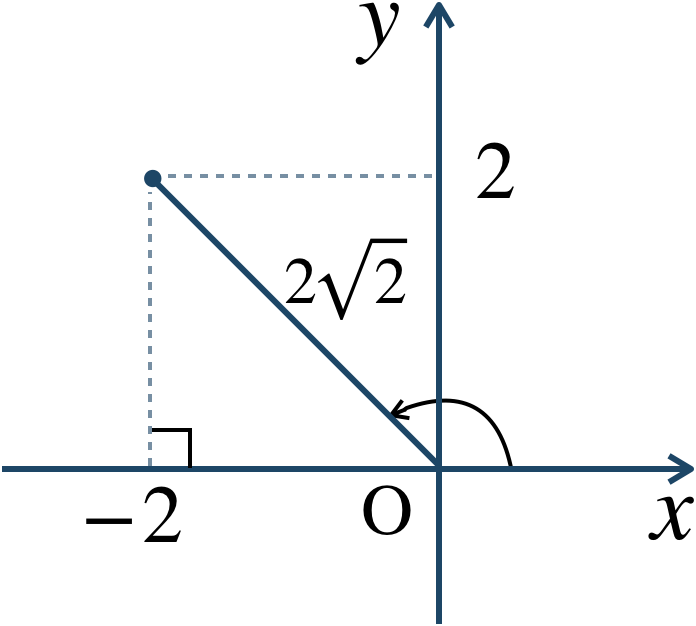
3点 \({\rm A}(-3+2i)~,~{\rm B}(2i)~,~{\rm C}(-9+8i)\) より、$$~~~\alpha=-3+2i~,~\beta=2i~,~\gamma=-9+8i$$とすると、次の複素数は、$$~~~~~~\frac{\,\gamma-\alpha \,}{\,\beta-\alpha \,}$$$$~=\frac{\,(-9+8i)-(-3+2i) \,}{\,2i-(-3+2i) \,}$$$$~=\frac{\,-9+8i+3-2i \,}{\,2i+3-2i \,}$$$$~=\frac{\,-6+6i \,}{\,3 \,}$$$$~=-2+2i$$これを極形式で表すと、絶対値は、$$~~~~~~|-2+2i|$$$$~=\sqrt{(-2)^2+2^2}$$$$~=\sqrt{4+4}=\sqrt{8}=2\sqrt{2}$$また、複素数平面上に表すと、
これより、偏角は \({\large \frac{\,3\,}{\,4\,}}\pi\) となる
よって、$$~~~2\sqrt{2}\left(\cos{\frac{\,3\,}{\,4 \,}\pi}+i\sin{\frac{\,3 \,}{\,4 \,}\pi}\right)$$\(\angle{\rm BAC}=\theta\) とすると、$$~~~\theta=\arg \left(\frac{\,\gamma-\alpha \,}{\,\beta-\alpha \,}\right)=\frac{\, 3\,}{\,4 \,}\pi$$したがって、答えは \({\large \frac{\,3\,}{\,4\,}}\pi\) となる。
今回のまとめ
複素数平面上の直線のなす角の求め方について解説しました。直線と実軸とのなす角なら \(\arg (\beta-\alpha)\) 、2直線のなす角なら \(\arg \left({\large \frac{\,\gamma-\alpha\,}{\,\beta-\alpha\,}}\right)\) で求めましょう。