角の二等分線と比

角の二等分線と比の関係公式
問題解説：角の二等分線と比
今回のまとめ

角の二等分線と比の関係公式

Point：内角の二等分線と比$\triangle {\rm ABC}$ と $\angle{\rm A}$ の内角の二等分線と直線 ${\rm BC}$ との交点を ${\rm D}$ とすると、

$${\rm AB}:{\rm AC}={\rm BD}:{\rm DC}$$

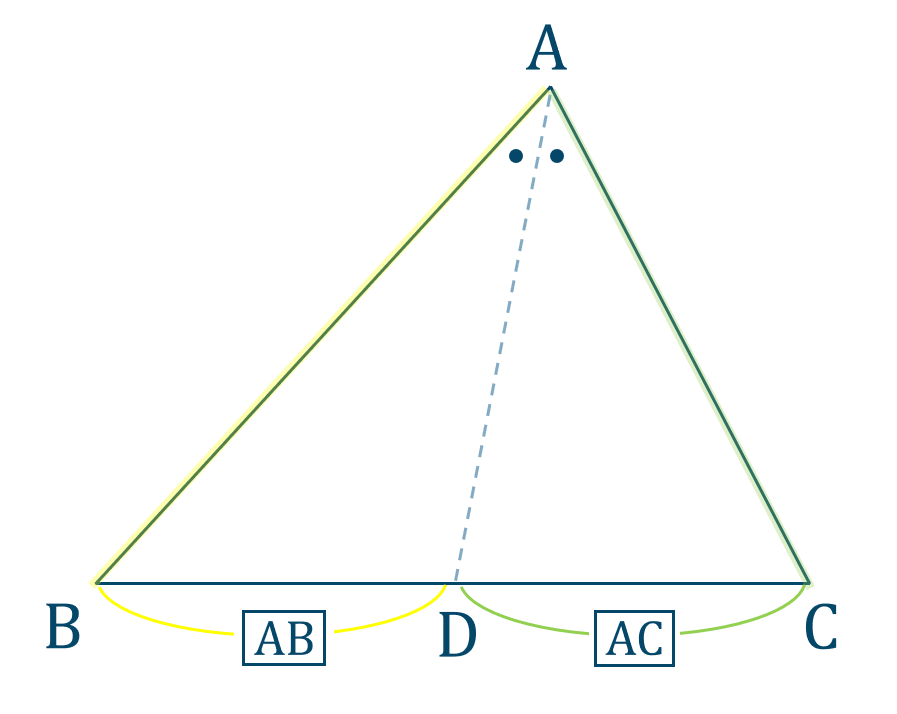
「${\rm A \to B}$ と ${\rm B \to D}$ の比」と
「${\rm A \to C}$ と ${\rm C \to D}$ の比」と覚えましょう。

Point：外角の二等分線と比

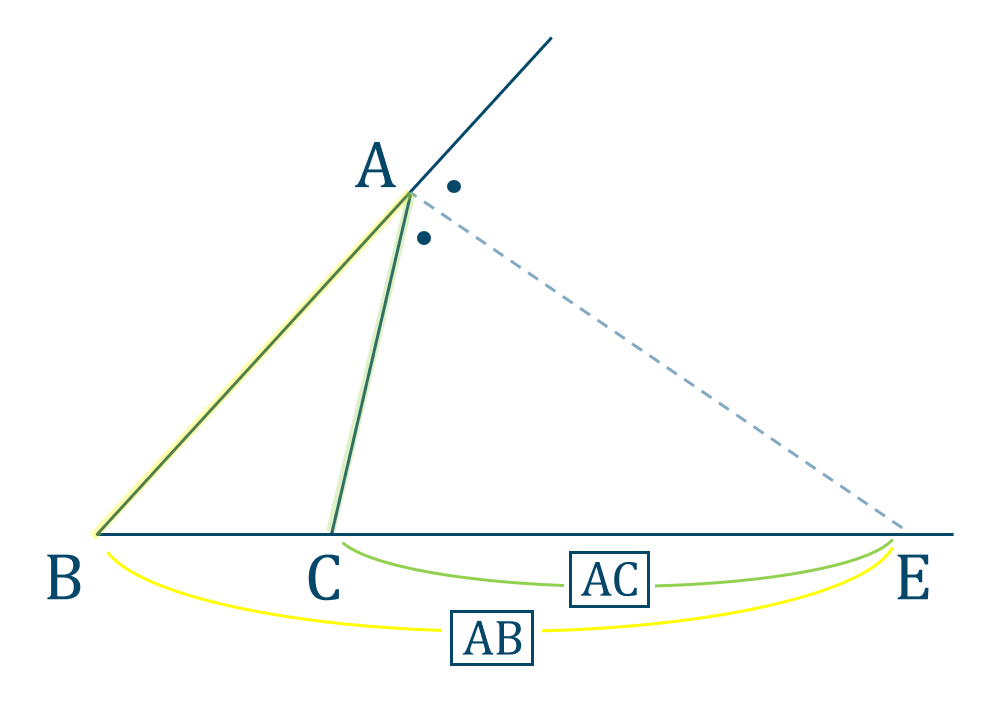
$\triangle {\rm ABC}$ と $\angle{\rm A}$ の外角の二等分線と直線 ${\rm BC}$ との交点を ${\rm E}$ とすると、

$${\rm AB}:{\rm AC}={\rm BE}:{\rm CE}$$

「${\rm A \to B}$ と ${\rm B \to E}$ の比」と
「${\rm A \to C}$ と ${\rm C \to E}$ の比」と覚えましょう。

問題解説：角の二等分線と比

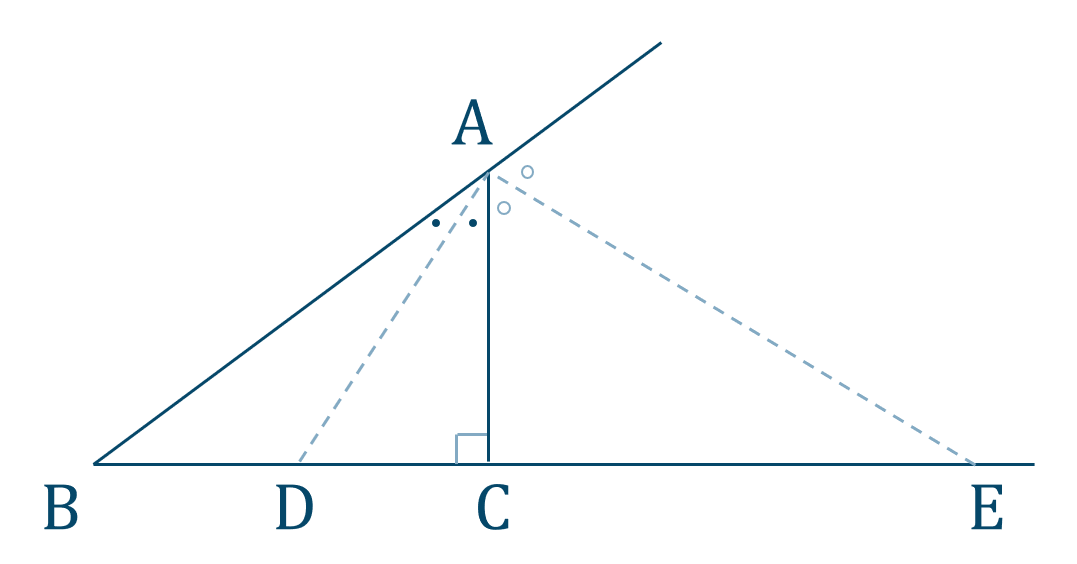
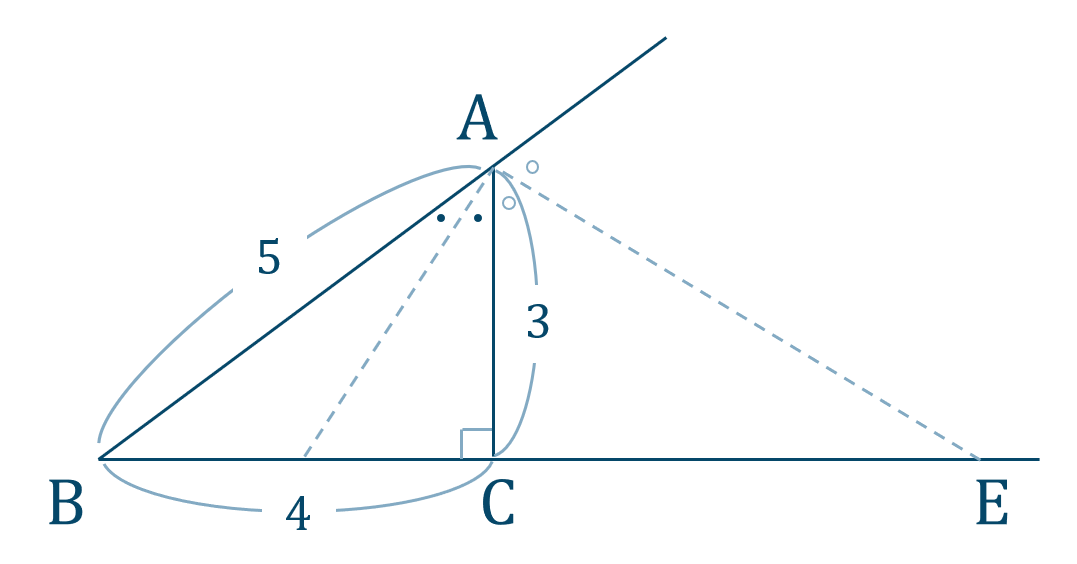
問題次の図で、$\angle{\rm C}=90^\circ$ $,$ ${\rm AB}=5$ $,$ ${\rm AC}=3$ で $\angle{\rm A}$ の内角の二等分線と直線 ${\rm BC}$ との交点を ${\rm D}$、$\angle{\rm A}$ の外角の二等分線と直線 ${\rm BC}$ との交点を ${\rm E}$ とするとき、${\rm DE}$ の長さを求めよ。

与えられた図は次のようになります。

$\triangle {\rm ABC}$ において、${\rm AB}=5$ $,$ ${\rm AC}=3$ より、三平方の定理を用いると、$$\hspace{ 10 pt}5^2={\rm BC}^2+3^2$$$$\hspace{ 10 pt}25={\rm BC}^2+9$$移項すると、$$\hspace{ 10 pt}-{\rm BC}^2=9-25$$$$\hspace{ 10 pt}-{\rm BC}^2=-16$$$$\hspace{ 17 pt} {\rm BC}^2=16$$${\rm BD}>0$ より、$$\hspace{ 10 pt} {\rm BC}=4$$
次に $\angle{\rm A}$ の内角の二等分線と比の関係より、
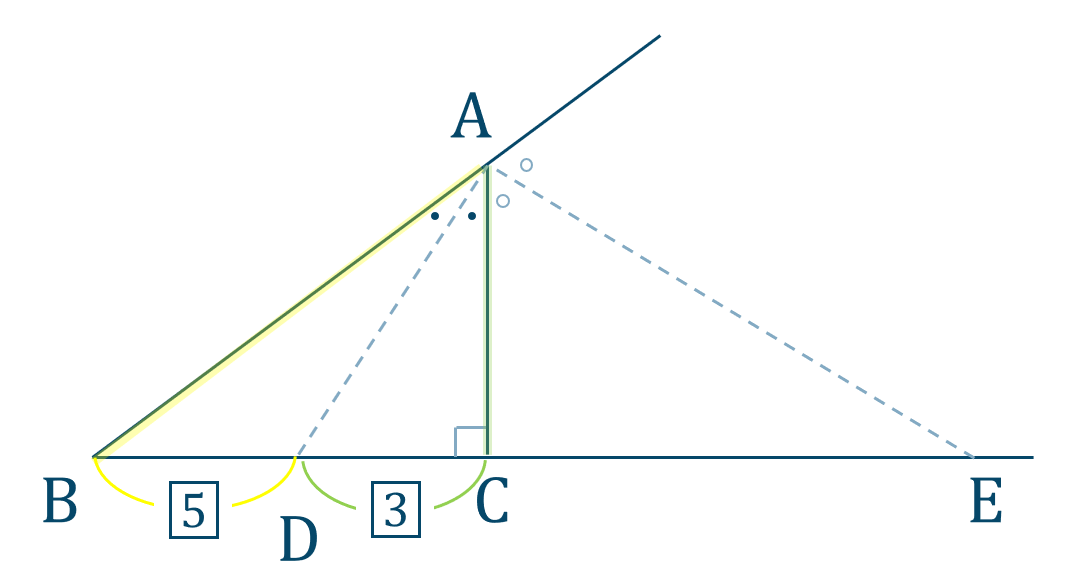
$$\hspace{ 10 pt}{\rm BD}:{\rm DC}=5:3$$よって、$$\hspace{ 10 pt}{\rm DC}=\frac{3}{8}{\rm BC}$$${\rm BC}=4$ より、$$\hspace{ 10 pt}{\rm DC}=\frac{3}{8}\times4$$$$\hspace{ 27 pt}=\frac{3}{2}$$
また、$\angle{\rm A}$ の外角の二等分線と比の関係より、
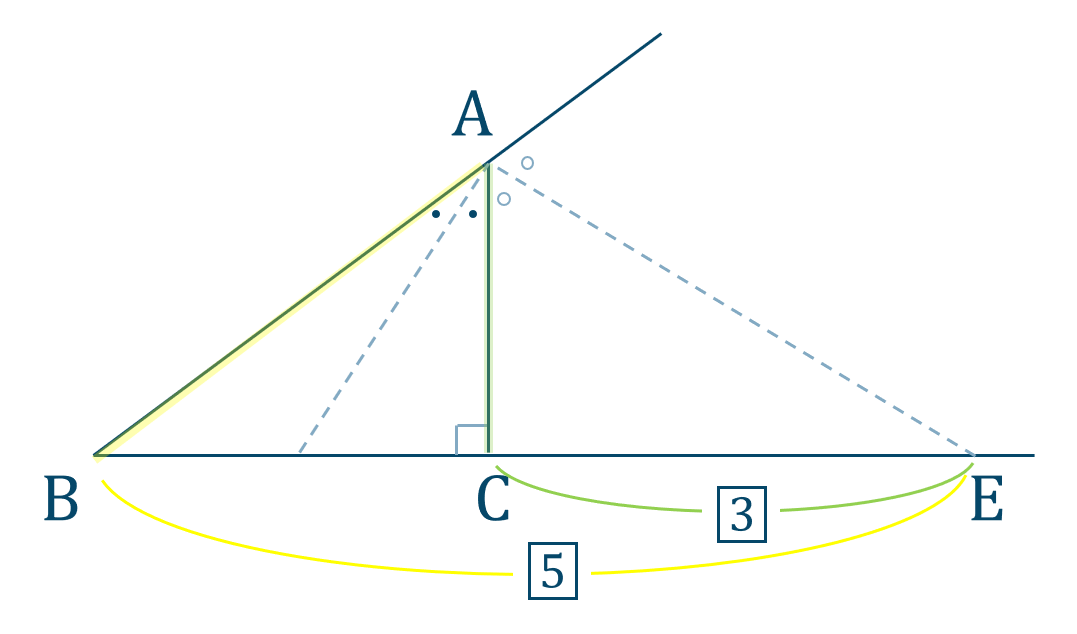
$$\hspace{ 10 pt}{\rm BE}:{\rm CE}=5:3$$これより、$$\hspace{ 10 pt}{\rm BC}:{\rm CE}=2:3$$よって、$$\hspace{ 10 pt}{\rm CE}=\frac{3}{2}{\rm BC}$$${\rm BC}=4$ を代入すると、$$\hspace{ 10 pt}{\rm CE}=\frac{3}{2}\times4$$$$\hspace{ 27 pt}=6$$
したがって、$$\hspace{ 10 pt}{\rm DE}={\rm DC}+{\rm CE}$$$$\hspace{ 27 pt}=\frac{3}{2}+6$$$$\hspace{ 27 pt}=\frac{3+12}{2}$$$$\hspace{ 27 pt}=\frac{15}{2}$$よって、答えは$$~~~{\rm DE}=\frac{15}{2}$$となります。