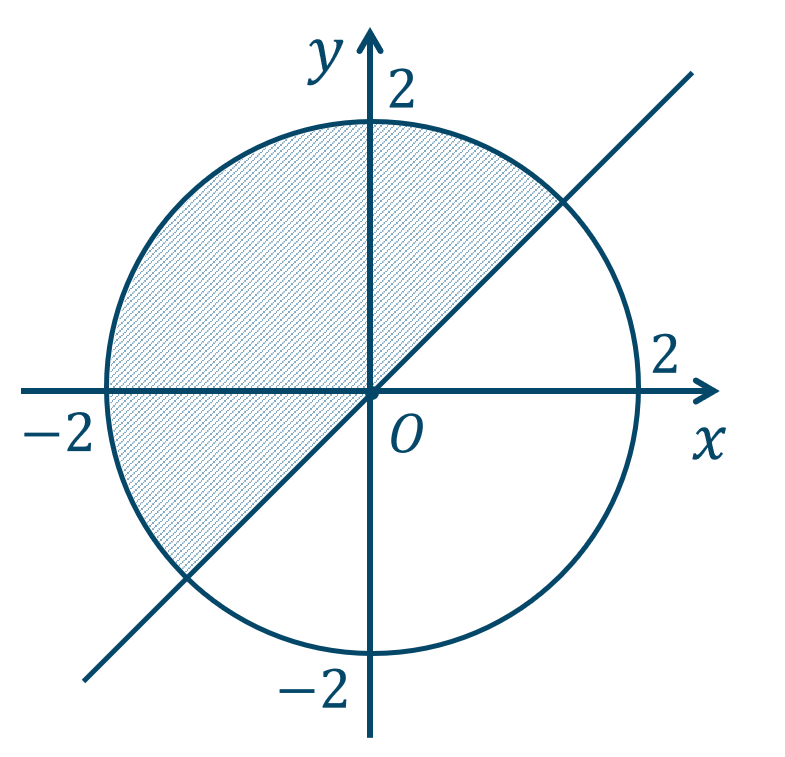文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
1章 方程式・式と証明
3章 三角関数
4章 指数関数・対数関数
5章 微分と積分
2章 図形と方程式
Readiness check
p.62
問1
\({\small (1)}~6\) \({\small (2)}~9\) \({\small (3)}~1\)
問1
\({\small (1)}~6\) \({\small (2)}~9\) \({\small (3)}~1\)
p.62
問2
\(10\)
問2
\(10\)
p.62
問3
\({\small (1)}~\)外心、外接円
\({\small (2)}~\)重心、\(2:1\)
\({\small (3)}~\)内心、内接円
問3
\({\small (1)}~\)外心、外接円
\({\small (2)}~\)重心、\(2:1\)
\({\small (3)}~\)内心、内接円
p.63
問4

\((3,1)\)
問4
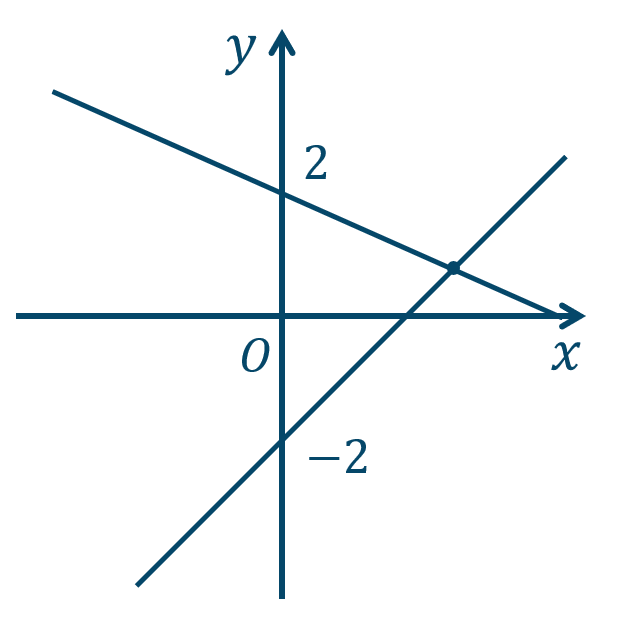
\((3,1)\)
p.63
問5
\(k=\pm6\sqrt{2}\)
問5
\(k=\pm6\sqrt{2}\)
p.63
問6
\(x>3\)
問6
\(x>3\)
1節 点と直線
p.64
問1
\({\small (1)}~8\) \({\small (2)}~7\)
問1
\({\small (1)}~8\) \({\small (2)}~7\)
p.65
問2

問2
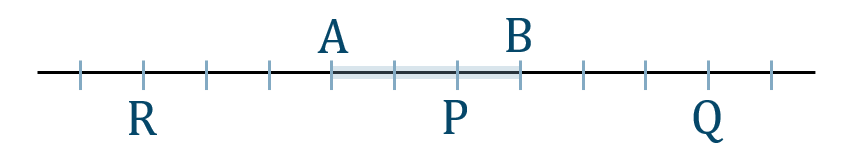
p.66
問3
\({\small (1)}~5\) \({\small (2)}~-3\) \({\small (3)}~{\large \frac{9}{2}}\)
→ 直線上の線分の長さ・内分点・外分点
問3
\({\small (1)}~5\) \({\small (2)}~-3\) \({\small (3)}~{\large \frac{9}{2}}\)
→ 直線上の線分の長さ・内分点・外分点
p.67
問4
A:第4象限 B:第2象限
C:第3象限 D:第1象限
問4
A:第4象限 B:第2象限
C:第3象限 D:第1象限
p.67
問5
\({\small (1)}~(5,4)\) \({\small (2)}~(-5,-4)\)
\({\small (3)}~(-5,4)\)
問5
\({\small (1)}~(5,4)\) \({\small (2)}~(-5,-4)\)
\({\small (3)}~(-5,4)\)
p.68
問6
\({\small (1)}~\sqrt{10}\) \({\small (2)}~5\)
\({\small (3)}~2\sqrt{5}\) \({\small (4)}~7\)
→ 平面上の線分の長さ
問6
\({\small (1)}~\sqrt{10}\) \({\small (2)}~5\)
\({\small (3)}~2\sqrt{5}\) \({\small (4)}~7\)
→ 平面上の線分の長さ
p.70
問7
\({\small (1)}~\)
\({\rm P}(6,5)~,~{\rm Q}(30,29)~,~{\rm M}\left({\large \frac{11}{2}},{\large \frac{9}{2}}\right)\)
\({\small (2)}~\)
\({\rm P}\left({\large \frac{18}{7}},{\large \frac{5}{7}}\right)~,~{\rm Q}(30,-13)~,~{\rm M}(2,1)\)
→ 平面上の内分点・外分点・重心
問7
\({\small (1)}~\)
\({\rm P}(6,5)~,~{\rm Q}(30,29)~,~{\rm M}\left({\large \frac{11}{2}},{\large \frac{9}{2}}\right)\)
\({\small (2)}~\)
\({\rm P}\left({\large \frac{18}{7}},{\large \frac{5}{7}}\right)~,~{\rm Q}(30,-13)~,~{\rm M}(2,1)\)
→ 平面上の内分点・外分点・重心
p.71
問9
\({\small (1)}~(1,2)\) \({\small (2)}~\left({\large \frac{7}{3}},-{\large \frac{5}{3}}\right)\)
→ 平面上の内分点・外分点・重心
問9
\({\small (1)}~(1,2)\) \({\small (2)}~\left({\large \frac{7}{3}},-{\large \frac{5}{3}}\right)\)
→ 平面上の内分点・外分点・重心
p.73
問11
\({\small (1)}~y=2x+7\)
\({\small (2)}~y=-3x+6\)
\({\small (3)}~x=-4\)
\({\small (4)}~y=5\)
→ 2点を通る直線の方程式
問11
\({\small (1)}~y=2x+7\)
\({\small (2)}~y=-3x+6\)
\({\small (3)}~x=-4\)
\({\small (4)}~y=5\)
→ 2点を通る直線の方程式
p.74
問12
\(2x+y-4=0\)
問12
\(2x+y-4=0\)
p.77
問13
互いに平行:②と③
互いに垂直:①と④
問13
互いに平行:②と③
互いに垂直:①と④
Training
p.81
1
\({\small (1)}~9\sqrt{2}\) \({\small (2)}~4\sqrt{5}\)
1
\({\small (1)}~9\sqrt{2}\) \({\small (2)}~4\sqrt{5}\)
p.81
2
\({\rm P}\left(-1,{\large \frac{10}{7}}\right)~,~{\rm Q}\left(-{\large \frac{23}{3}},-10\right)\)
2
\({\rm P}\left(-1,{\large \frac{10}{7}}\right)~,~{\rm Q}\left(-{\large \frac{23}{3}},-10\right)\)
p.81
3
\((-4,-1)\)
3
\((-4,-1)\)
p.81
4
\((1,3)\)
4
\((1,3)\)
p.81
5
\({\small (1)}~y=-{\large \frac{2}{3}}x+3\)
\({\small (2)}~x=-2\)
5
\({\small (1)}~y=-{\large \frac{2}{3}}x+3\)
\({\small (2)}~x=-2\)
p.81
6
\(x+2y=0\)
6
\(x+2y=0\)
p.81
7
平行 \(3x-2y-1=0\)
垂直 \(2x+3y-18=0\)
7
平行 \(3x-2y-1=0\)
垂直 \(2x+3y-18=0\)
p.81
8
\((0,1)\)
8
\((0,1)\)
p.81
9
\({\small (1)}~{\large \frac{5\sqrt{10}}{4}}\) \({\small (2)}~2\sqrt{2}\)
9
\({\small (1)}~{\large \frac{5\sqrt{10}}{4}}\) \({\small (2)}~2\sqrt{2}\)
2節 円
p.82
問1
\({\small (1)}~(x-2)^2+(y+1)^2=9\)
\({\small (2)}~x^2+y^2=4\)
問1
\({\small (1)}~(x-2)^2+(y+1)^2=9\)
\({\small (2)}~x^2+y^2=4\)
p.83
問4
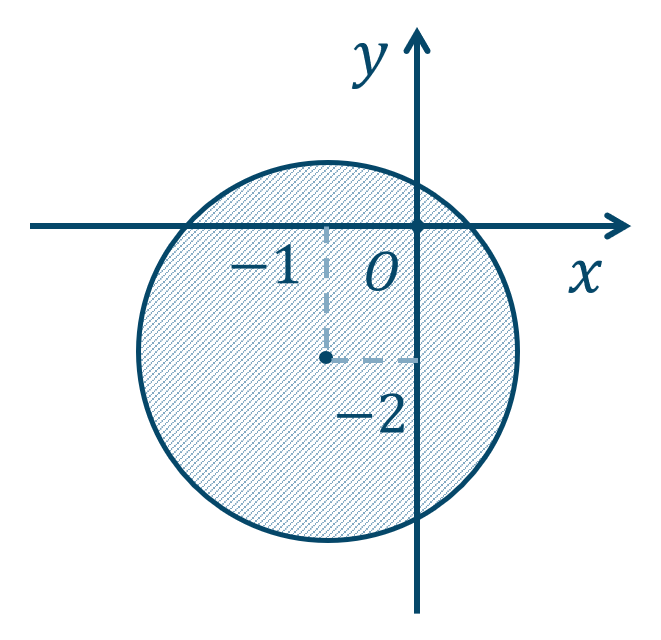
\({\small (1)}~\)中心 \((3,-2)\)、半径 \(3\) の円
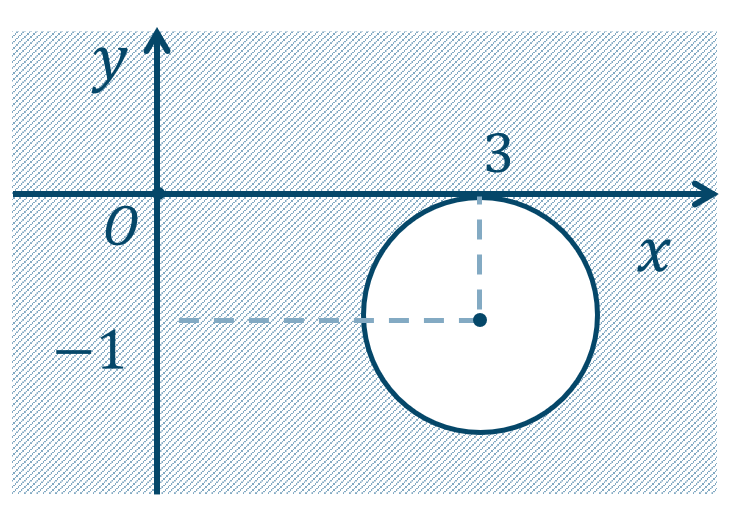
\({\small (2)}~\)中心 \((-1,0)\)、半径 \(1\) の円
→ 円の方程式
問4
\({\small (1)}~\)中心 \((3,-2)\)、半径 \(3\) の円
\({\small (2)}~\)中心 \((-1,0)\)、半径 \(1\) の円
→ 円の方程式
p.86
問7
\(k<-5\sqrt{2}~,~5\sqrt{2}<k\)
問7
\(k<-5\sqrt{2}~,~5\sqrt{2}<k\)
p.88
問9
\({\small (1)}~3x+y-10=0\)
\({\small (2)}~2x-3y+13=0\)
\({\small (3)}~x=3\)
問9
\({\small (1)}~3x+y-10=0\)
\({\small (2)}~2x-3y+13=0\)
\({\small (3)}~x=3\)
p.91
参考1
\({\small (1)}~x^2+y^2-x+{\large \frac{1}{3}}y-{\large \frac{10}{3}}=0\)
\({\small (2)}~3x-y-2=0\)
→ 2つの円の交点を通る円・直線
参考1
\({\small (1)}~x^2+y^2-x+{\large \frac{1}{3}}y-{\large \frac{10}{3}}=0\)
\({\small (2)}~3x-y-2=0\)
→ 2つの円の交点を通る円・直線
Training
p.92
10
\({\small (1)}~(x+4)^2+(y-3)^2=9\)
\({\small (2)}~x^2+(y-2)^2=5\)
10
\({\small (1)}~(x+4)^2+(y-3)^2=9\)
\({\small (2)}~x^2+(y-2)^2=5\)
p.92
11
\({\small (1)}~\)中心 \((-2,5)\)、半径 \(6\)
\({\small (2)}~\)中心 \(\left(0,-{\large \frac{5}{2}}\right)\)、半径 \({\large \frac{\sqrt{17}}{2}}\)
11
\({\small (1)}~\)中心 \((-2,5)\)、半径 \(6\)
\({\small (2)}~\)中心 \(\left(0,-{\large \frac{5}{2}}\right)\)、半径 \({\large \frac{\sqrt{17}}{2}}\)
p.92
12
\(x^2+y^2-8x-8y+12=0\)
中心 \((4,4)\)、半径 \(2\sqrt{5}\)
12
\(x^2+y^2-8x-8y+12=0\)
中心 \((4,4)\)、半径 \(2\sqrt{5}\)
p.92
13
\({\small (1)}~(-2,3)~,~(3,-2)\)
\({\small (2)}~(-2,1)\)
13
\({\small (1)}~(-2,3)~,~(3,-2)\)
\({\small (2)}~(-2,1)\)
p.92
14
\(-3\sqrt{10}<k<3\sqrt{10}\) のとき、
共有点2個
\(k=\pm3\sqrt{10}\) のとき、
共有点1個
\(k<-3\sqrt{10}~,~3\sqrt{10}<k\) のとき、
共有点0個
14
\(-3\sqrt{10}<k<3\sqrt{10}\) のとき、
共有点2個
\(k=\pm3\sqrt{10}\) のとき、
共有点1個
\(k<-3\sqrt{10}~,~3\sqrt{10}<k\) のとき、
共有点0個
p.92
15
\({\small (1)}~x-3y+10=0\)
\({\small (2)}~y=4\)
15
\({\small (1)}~x-3y+10=0\)
\({\small (2)}~y=4\)
p.92
16
\(x+7y-50=0~,~x-y-10=0\)
16
\(x+7y-50=0~,~x-y-10=0\)
p.92
17
\({\small (1)}~r=4\)
\({\small (2)}~4<r<6\)
17
\({\small (1)}~r=4\)
\({\small (2)}~4<r<6\)
3節 軌跡と領域
p.94
問1
直線 \(3x-5y+8=0\)
問1
直線 \(3x-5y+8=0\)
p.94
問2
中心が原点、半径 \(4\) の円
問2
中心が原点、半径 \(4\) の円
p.95
問4
直線 \(y=2x-3\)
問4
直線 \(y=2x-3\)
p.97
問6
\({\small (1)}~\)

境界線を含まない
\({\small (2)}~\)

境界線を含まない
\({\small (3)}~\)

境界線を含む
\({\small (4)}~\)

境界線を含む
問6
\({\small (1)}~\)
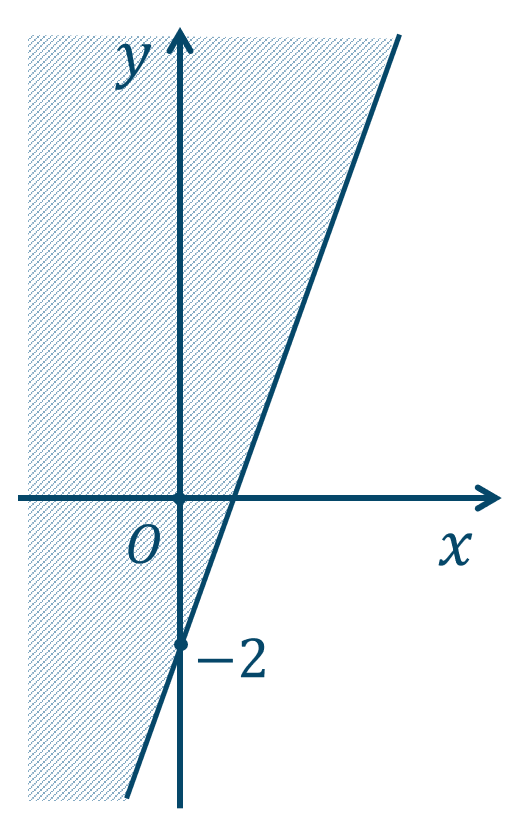
境界線を含まない
\({\small (2)}~\)
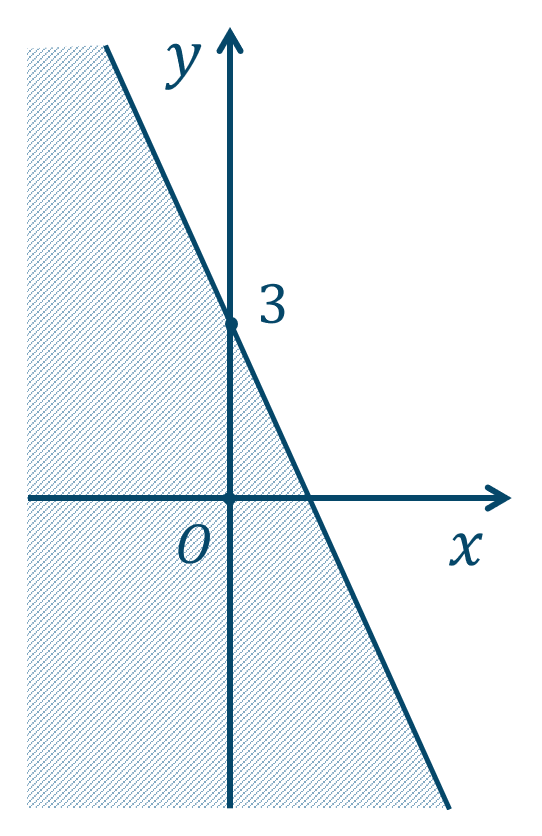
境界線を含まない
\({\small (3)}~\)
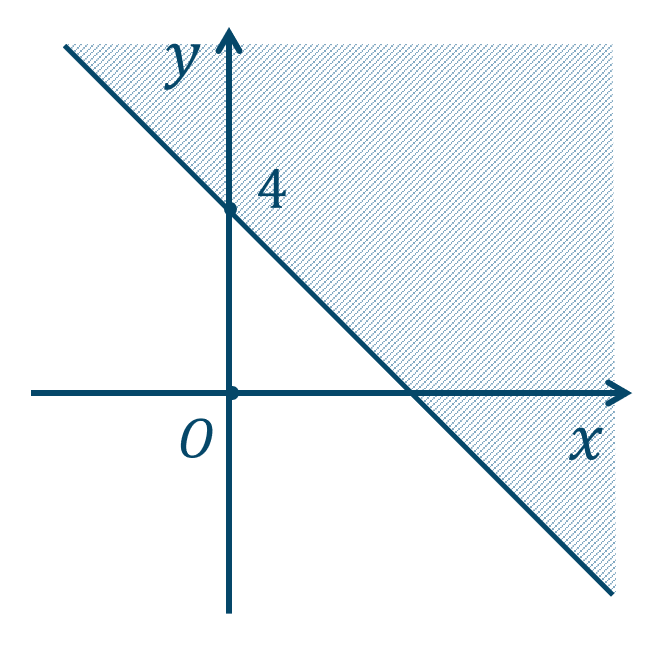
境界線を含む
\({\small (4)}~\)
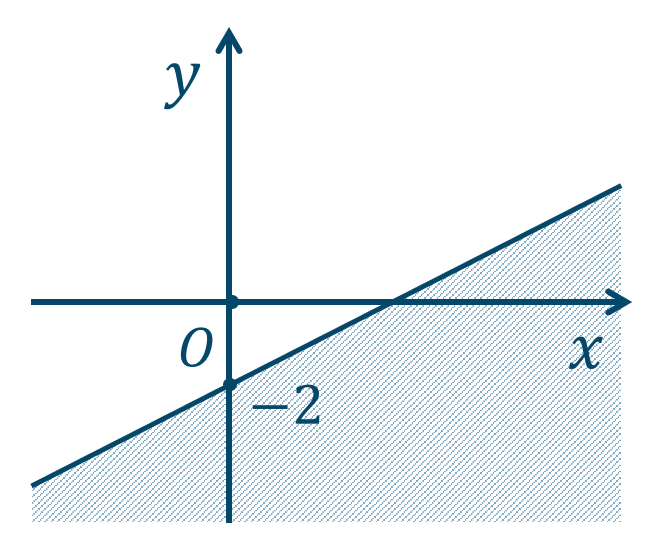
境界線を含む
p.97
問7
\({\small (1)}~\)

境界線を含まない
\({\small (2)}~\)

境界線を含む
問7
\({\small (1)}~\)
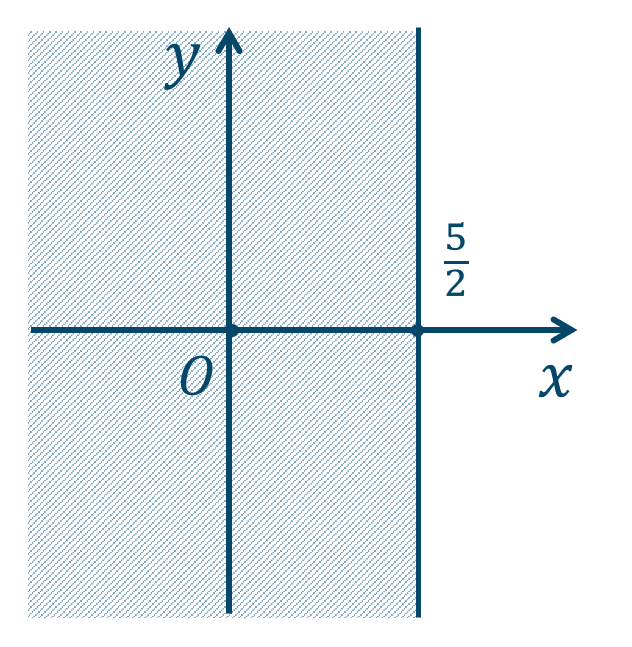
境界線を含まない
\({\small (2)}~\)
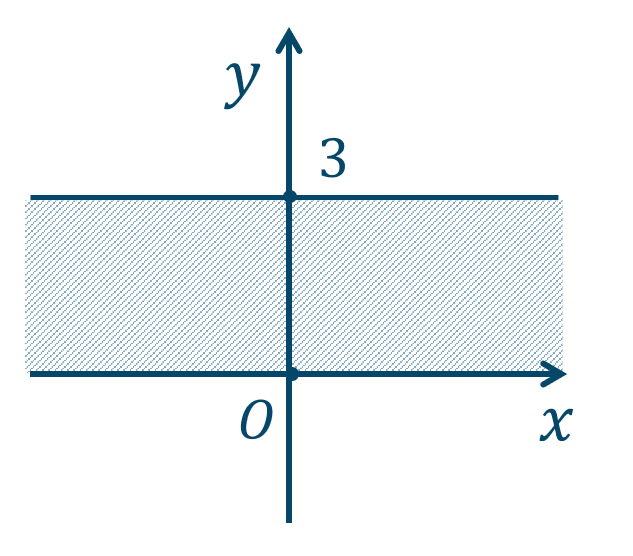
境界線を含む
p.98
問8
\({\small (1)}~\)

境界線を含まない
\({\small (2)}~\)

境界線を含む
問8
\({\small (1)}~\)
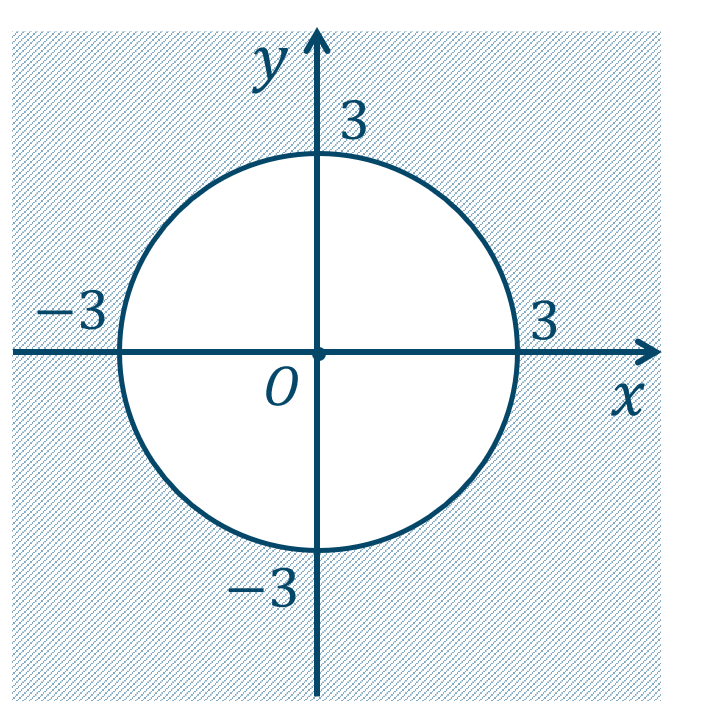
境界線を含まない
\({\small (2)}~\)

境界線を含む
p.99
問10
\({\small (1)}~\)

境界線を含まない
\({\small (2)}~\)

境界線を含む
問10
\({\small (1)}~\)
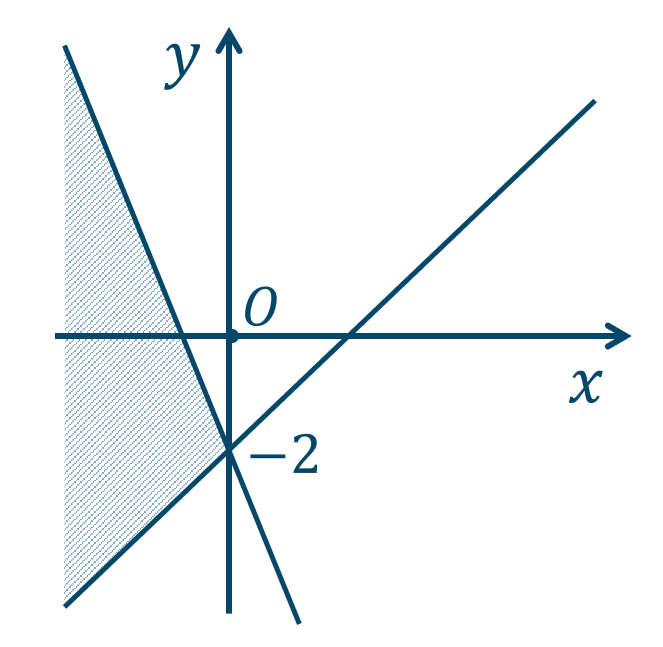
境界線を含まない
\({\small (2)}~\)
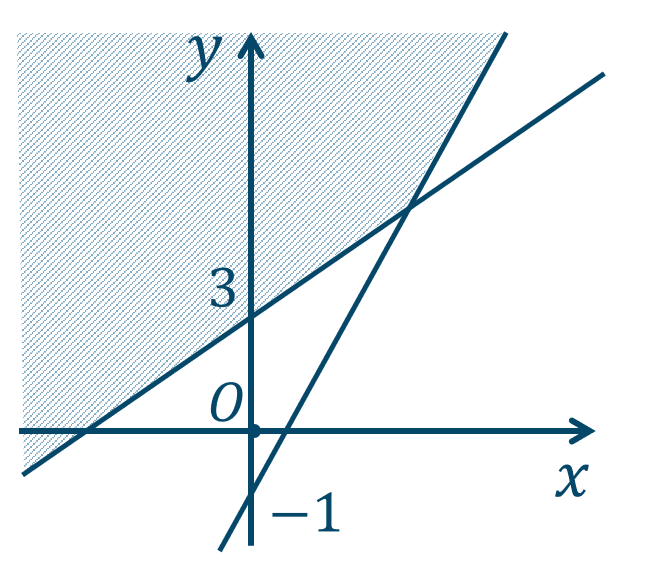
境界線を含む
p.99
問11
第1象限 \(x>0~,~y>0\)
第2象限 \(x<0~,~y>0\)
第3象限 \(x<0~,~y<0\)
第4象限 \(x>0~,~y<0\)
問11
第1象限 \(x>0~,~y>0\)
第2象限 \(x<0~,~y>0\)
第3象限 \(x<0~,~y<0\)
第4象限 \(x>0~,~y<0\)
p.102
問1
challenge
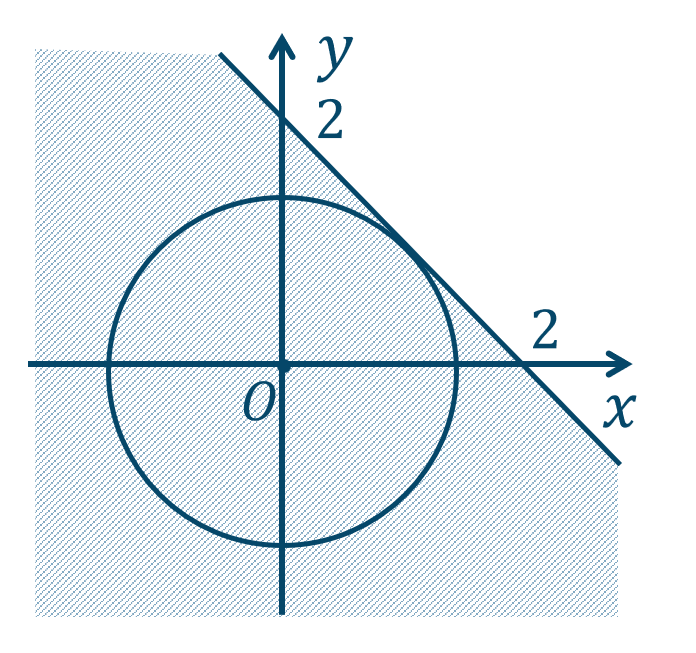
[証明] \(x^2+y^2<2\) の領域を \(P\)、\(x+y<2\) の領域を \(Q\) とする
これらの領域を図示すると次の図のようになる

これより、\(P\subset Q\) が成り立つ
したがって、
\(x^2+y^2<2\) ならば \(x+y<2\)
[終]
→ 領域を用いた証明
問1
challenge
[証明] \(x^2+y^2<2\) の領域を \(P\)、\(x+y<2\) の領域を \(Q\) とする
これらの領域を図示すると次の図のようになる
これより、\(P\subset Q\) が成り立つ
したがって、
\(x^2+y^2<2\) ならば \(x+y<2\)
[終]
→ 領域を用いた証明
Training
p.103
18
直線 \(x=2\)
18
直線 \(x=2\)
p.103
19
中心が\((-3,0)\)、半径 \(3\) の円
19
中心が\((-3,0)\)、半径 \(3\) の円
p.103
20
\({\small (1)}~\)
中心が\(\left({\large \frac{5}{2}},1\right)\)、半径 \(\sqrt{3}\) の円
\({\small (2)}~\)
直線 \(x-2y+2=0\)
20
\({\small (1)}~\)
中心が\(\left({\large \frac{5}{2}},1\right)\)、半径 \(\sqrt{3}\) の円
\({\small (2)}~\)
直線 \(x-2y+2=0\)
p.103
21
\({\small (1)}~\)

境界線を含まない
\({\small (2)}~\)

境界線を含む
\({\small (3)}~\)

境界線を含まない
21
\({\small (1)}~\)
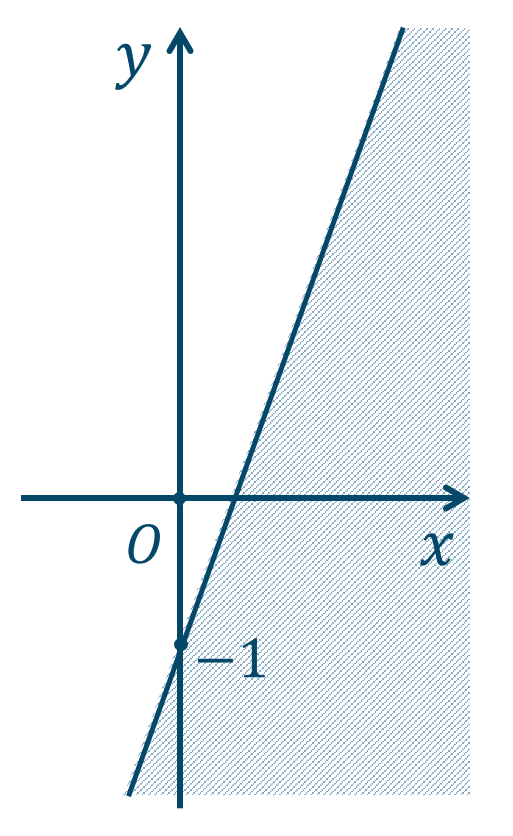
境界線を含まない
\({\small (2)}~\)
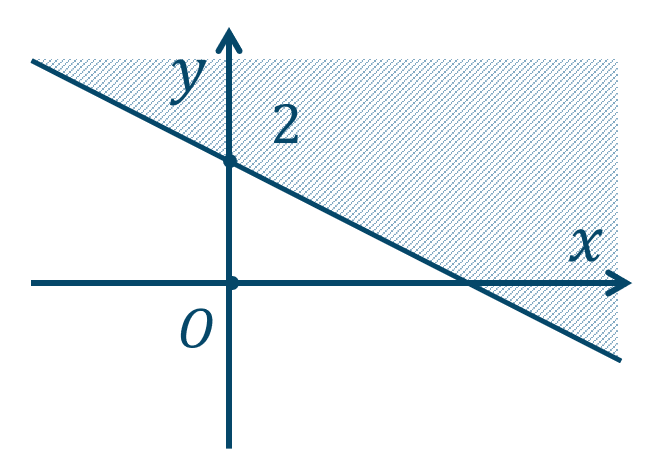
境界線を含む
\({\small (3)}~\)
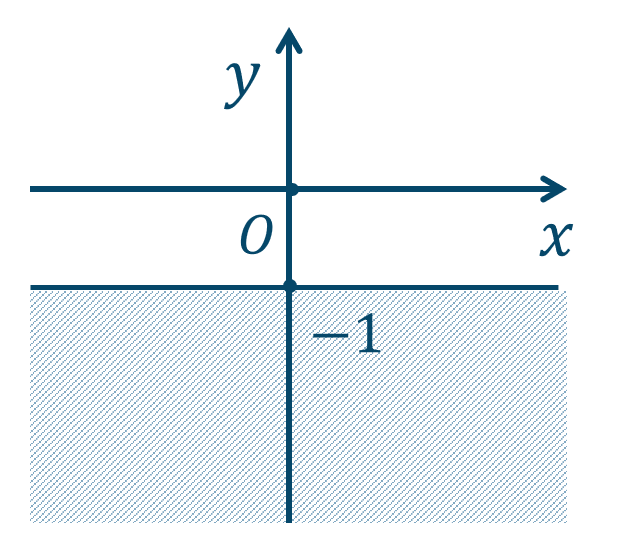
境界線を含まない
p.103
22
\({\small (1)}~\)

境界線を含まない
\({\small (2)}~\)

境界線を含む
22
\({\small (1)}~\)
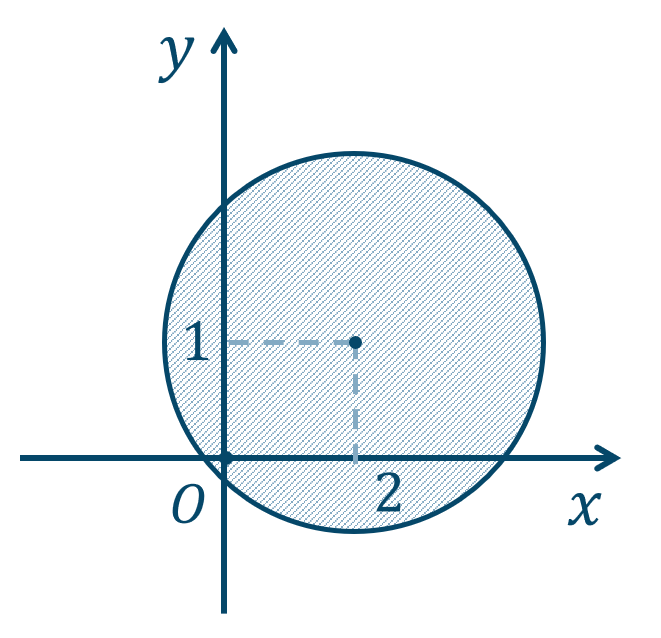
境界線を含まない
\({\small (2)}~\)
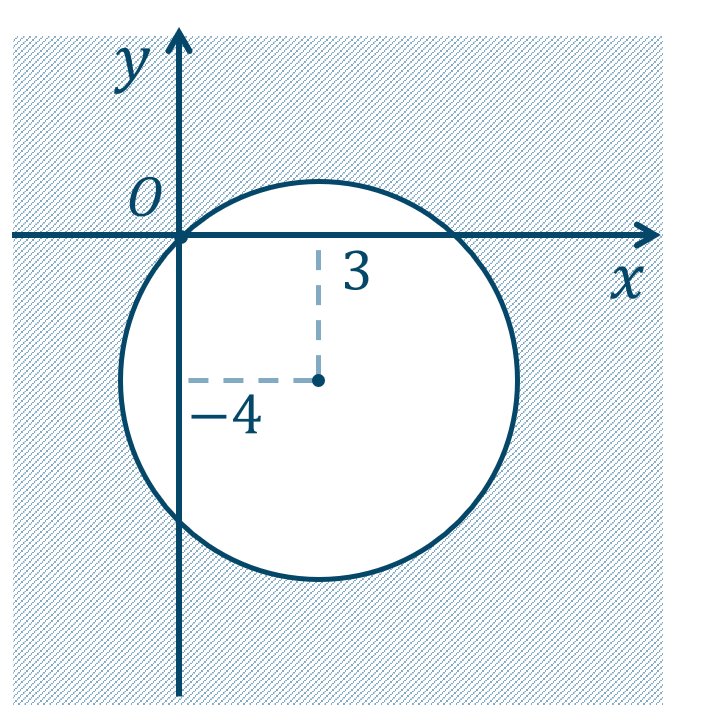
境界線を含む
p.103
23
\({\small (1)}~\)

境界線を含む
\({\small (2)}~\)

境界線を含まない
\({\small (3)}~\)

境界線を含む
23
\({\small (1)}~\)

境界線を含む
\({\small (2)}~\)
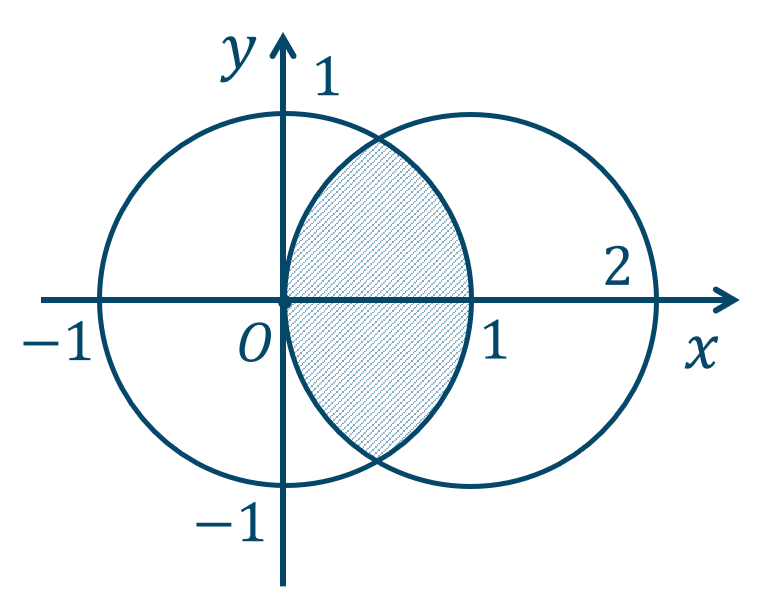
境界線を含まない
\({\small (3)}~\)
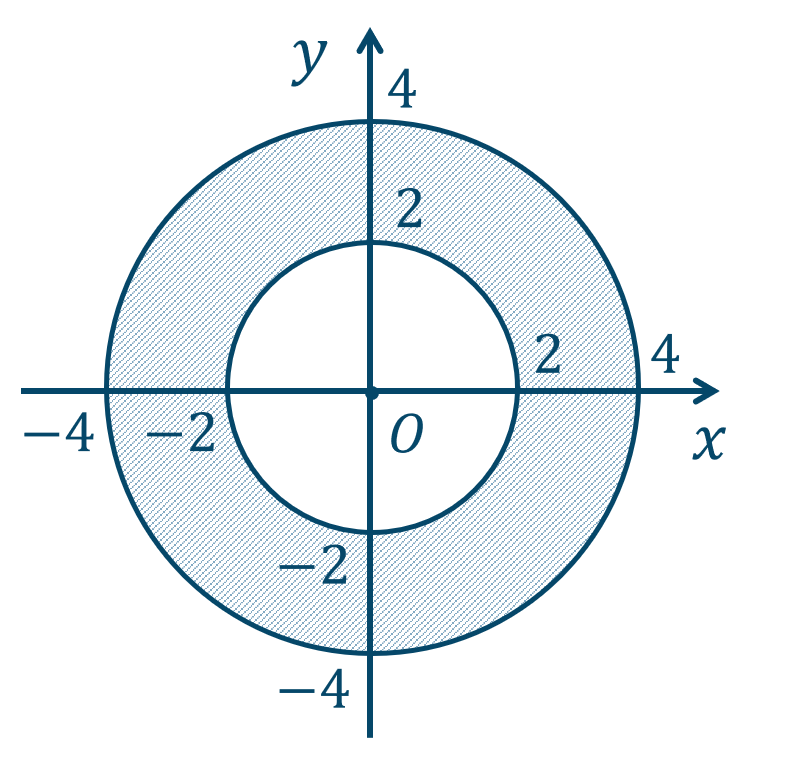
境界線を含む
p.103
24

境界線を含まない
24
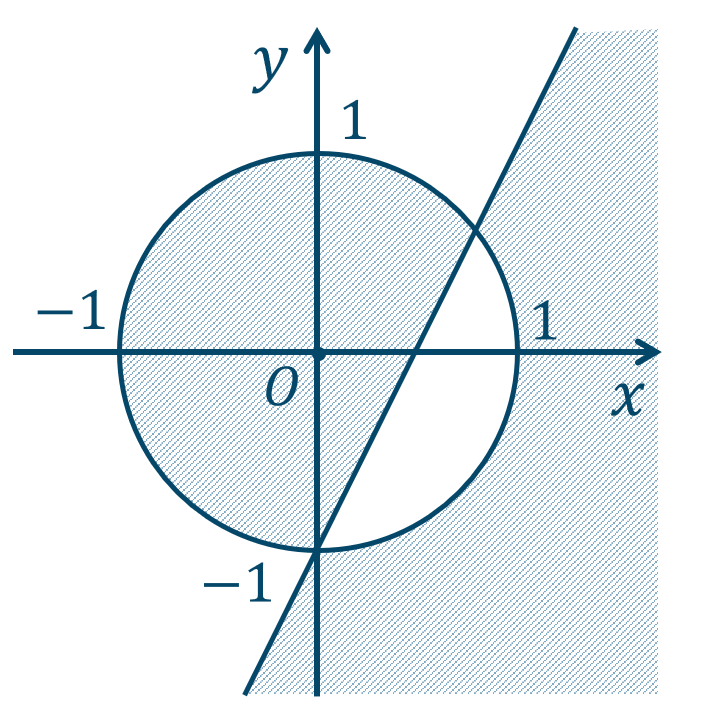
境界線を含まない
p.103
25
最大値 \(2~(x=2~,~y=4)\)
最小値 \(-4~(x=5~,~y=1)\)
25
最大値 \(2~(x=2~,~y=4)\)
最小値 \(-4~(x=5~,~y=1)\)
Level Up 図形と方程式
p.104
1
\((3,0)\)
1
\((3,0)\)
p.104
3
\(a=1\)
3
\(a=1\)
p.104
4
\({\small (1)}~\)
それぞれの直線の傾きは、
\(-{\large \frac{a}{b}}~,~-{\large \frac{a’}{b’}}\)
これより、2直線が平行となるので、
\(-{\large \frac{a}{b}}=-{\large \frac{a’}{b’}}\)
式変形すると、
\(ab’-a’b=0\)
したがって、
2直線が平行\(~~\Leftrightarrow~~ab’-a’b=0\)
\({\small (2)}~\)
それぞれの直線の傾きは、
\(-{\large \frac{a}{b}}~,~-{\large \frac{a’}{b’}}\)
これより、2直線が垂直となるので、
\(\left(-{\large \frac{a}{b}}\right)\left(-{\large \frac{a’}{b’}}\right)=-1\)
式変形すると、
\(aa’+bb’=0\)
したがって、
2直線が垂直\(~~\Leftrightarrow~~aa’+bb’=0\)
4
\({\small (1)}~\)
それぞれの直線の傾きは、
\(-{\large \frac{a}{b}}~,~-{\large \frac{a’}{b’}}\)
これより、2直線が平行となるので、
\(-{\large \frac{a}{b}}=-{\large \frac{a’}{b’}}\)
式変形すると、
\(ab’-a’b=0\)
したがって、
2直線が平行\(~~\Leftrightarrow~~ab’-a’b=0\)
\({\small (2)}~\)
それぞれの直線の傾きは、
\(-{\large \frac{a}{b}}~,~-{\large \frac{a’}{b’}}\)
これより、2直線が垂直となるので、
\(\left(-{\large \frac{a}{b}}\right)\left(-{\large \frac{a’}{b’}}\right)=-1\)
式変形すると、
\(aa’+bb’=0\)
したがって、
2直線が垂直\(~~\Leftrightarrow~~aa’+bb’=0\)
p.104
6
\({\small (1)}~5\) \({\small (2)}~{\large \frac{22}{5}}\) \({\small (3)}~11\)
6
\({\small (1)}~5\) \({\small (2)}~{\large \frac{22}{5}}\) \({\small (3)}~11\)
p.105
7
\({\small (1)}~(x-3)^2+(y-2)^2=5\)
\({\small (2)}~(x-1)^2+(y-1)^2=1\)
または
\((x-5)^2+(y-5)^2=25\)
7
\({\small (1)}~(x-3)^2+(y-2)^2=5\)
\({\small (2)}~(x-1)^2+(y-1)^2=1\)
または
\((x-5)^2+(y-5)^2=25\)
p.105
8
\(m<-\sqrt{15}~,~\sqrt{15}<m\)
8
\(m<-\sqrt{15}~,~\sqrt{15}<m\)
p.105
10
\(y=x~,~y=-x\)
10
\(y=x~,~y=-x\)
p.105
11
中心が\((1,2)\)、半径 \(3\) の円
11
中心が\((1,2)\)、半径 \(3\) の円
p.105
12
中心が\((4,0)\)、半径 \(1\) の円
12
中心が\((4,0)\)、半径 \(1\) の円
p.105
13
\({\small (1)}~y<x+1~,~y>4x-8\)
\(~~~~~~y>-{\large \frac{1}{2}}x+1\)
\({\small (2)}~x^2+y^2>1~,~(x-1)^2+y^2<4\)
13
\({\small (1)}~y<x+1~,~y>4x-8\)
\(~~~~~~y>-{\large \frac{1}{2}}x+1\)
\({\small (2)}~x^2+y^2>1~,~(x-1)^2+y^2<4\)
p.105
14
最大値 \(11~(x=4~,~y=-3)\)
最小値 \(-5~(x=-2~,~y=1)\)
14
最大値 \(11~(x=4~,~y=-3)\)
最小値 \(-5~(x=-2~,~y=1)\)
次のページ「3章 三角関数」