文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
1章 方程式・式と証明
2章 図形と方程式
4章 指数関数・対数関数
5章 微分と積分
3章 三角関数
Readiness check
p.108 問1
| \(\theta\) | \(0^\circ\) | \(30^\circ\) | \(45^\circ\) | \(60^\circ\) | \(90^\circ\) |
| \(\sin{}\) | \(0\) | \({\large \frac{1}{2}}\) | \({\large \frac{1}{\sqrt{2}}}\) | \({\large \frac{\sqrt{3}}{2}}\) | \(1\) |
| \(\cos{}\) | \(1\) | \({\large \frac{\sqrt{3}}{2}}\) | \({\large \frac{1}{\sqrt{2}}}\) | \({\large \frac{1}{2}}\) | \(0\) |
| \(\tan{}\) | \(0\) | \({\large \frac{1}{\sqrt{3}}}\) | \(1\) | \(\sqrt{3}\) | ー |
| \(\theta\) | \(120^\circ\) | \(135^\circ\) | \(150^\circ\) | \(180^\circ\) |
| \(\sin{}\) | \({\large \frac{\sqrt{3}}{2}}\) | \({\large \frac{1}{\sqrt{2}}}\) | \({\large \frac{1}{2}}\) | \(0\) |
| \(\cos{}\) | \(-{\large \frac{1}{2}}\) | \(-{\large \frac{1}{\sqrt{2}}}\) | \(-{\large \frac{\sqrt{3}}{2}}\) | \(-1\) |
| \(\tan{}\) | \(-\sqrt{3}\) | \(-1\) | \(-{\large \frac{1}{\sqrt{3}}}\) | \(0\) |
p.108 問2
\({\small (1)}~\cos{22^\circ}\) \({\small (2)}~\sin{22^\circ}\)
\({\small (3)}~{\large \frac{1}{\tan{22^\circ}}}\) \({\small (4)}~\sin{31^\circ}\)
\({\small (5)}~-\cos{31^\circ}\) \({\small (6)}~-\tan{31^\circ}\)
\({\small (1)}~\cos{22^\circ}\) \({\small (2)}~\sin{22^\circ}\)
\({\small (3)}~{\large \frac{1}{\tan{22^\circ}}}\) \({\small (4)}~\sin{31^\circ}\)
\({\small (5)}~-\cos{31^\circ}\) \({\small (6)}~-\tan{31^\circ}\)
p.109 問3
\({\small (1)}~45^\circ~,~135^\circ\) \({\small (2)}~150^\circ\) \({\small (3)}~135^\circ\)
\({\small (1)}~45^\circ~,~135^\circ\) \({\small (2)}~150^\circ\) \({\small (3)}~135^\circ\)
p.109 問4
\({\small (1)}~\)
\(\sin{\theta}={\large \frac{3}{5}}~,~\tan{\theta}=-{\large \frac{3}{4}}\)
\({\small (2)}~\)
\(\theta\) が鋭角のとき
\(\cos{\theta}={\large \frac{\sqrt{6}}{3}}~,~\tan{\theta}={\large \frac{\sqrt{2}}{2}}\)
\(\theta\) が鈍角のとき
\(\cos{\theta}=-{\large \frac{\sqrt{6}}{3}}~,~\tan{\theta}=-{\large \frac{\sqrt{2}}{2}}\)
\({\small (3)}~\)
\(\cos{\theta}={\large \frac{\sqrt{5}}{3}}~,~\sin{\theta}={\large \frac{2}{3}}\)
\({\small (1)}~\)
\(\sin{\theta}={\large \frac{3}{5}}~,~\tan{\theta}=-{\large \frac{3}{4}}\)
\({\small (2)}~\)
\(\theta\) が鋭角のとき
\(\cos{\theta}={\large \frac{\sqrt{6}}{3}}~,~\tan{\theta}={\large \frac{\sqrt{2}}{2}}\)
\(\theta\) が鈍角のとき
\(\cos{\theta}=-{\large \frac{\sqrt{6}}{3}}~,~\tan{\theta}=-{\large \frac{\sqrt{2}}{2}}\)
\({\small (3)}~\)
\(\cos{\theta}={\large \frac{\sqrt{5}}{3}}~,~\sin{\theta}={\large \frac{2}{3}}\)
1節 三角関数
p.110 問1
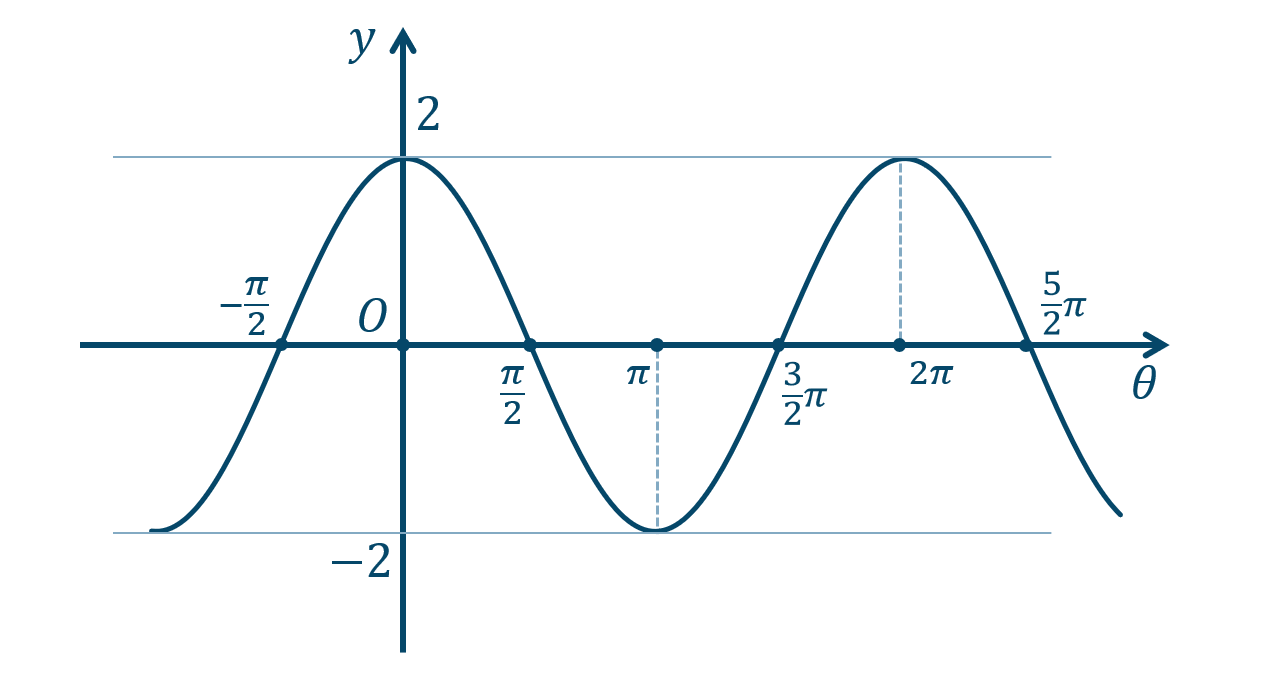
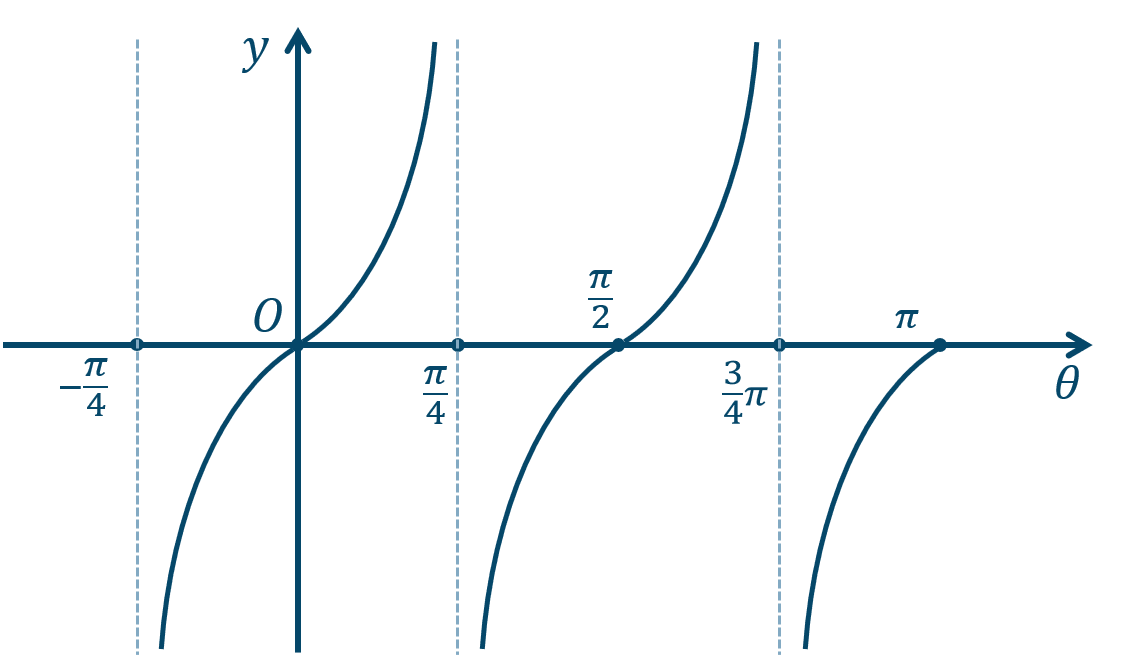
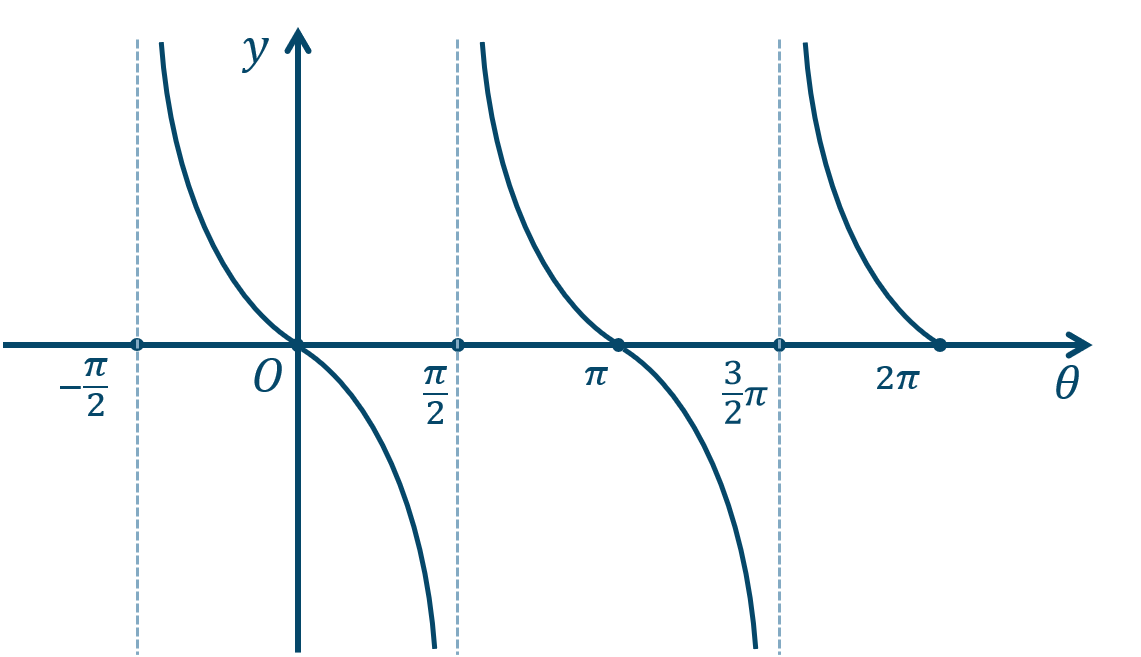
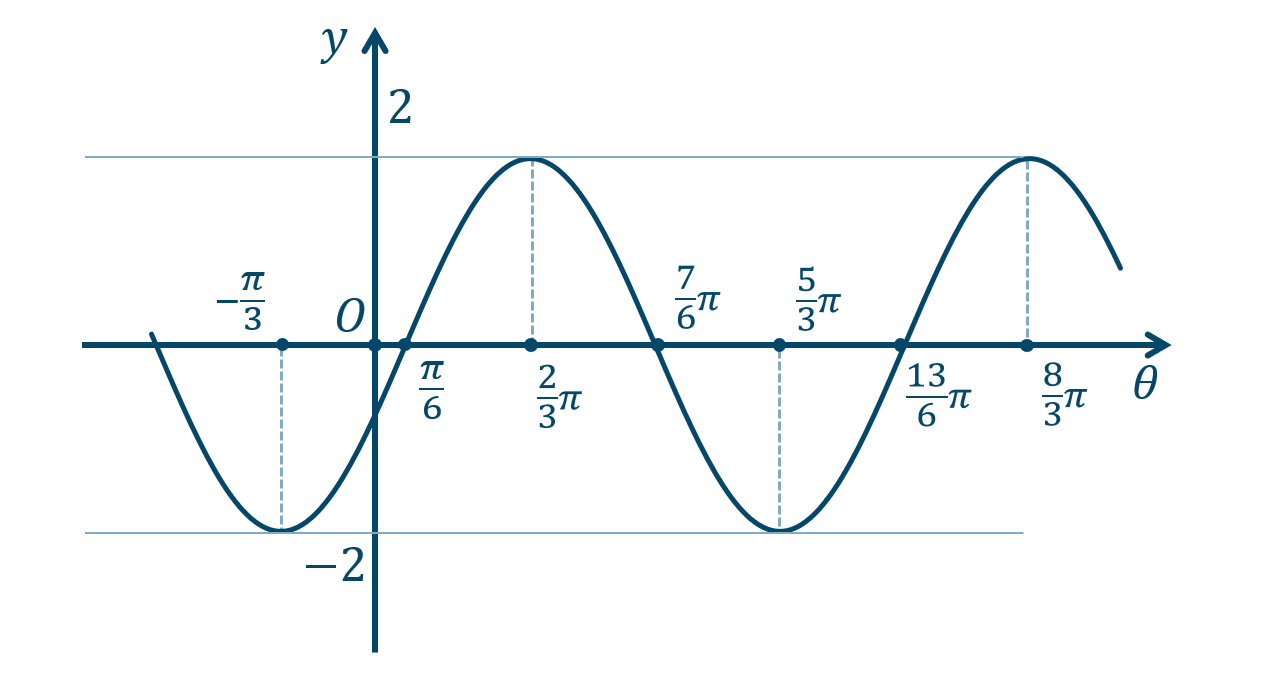
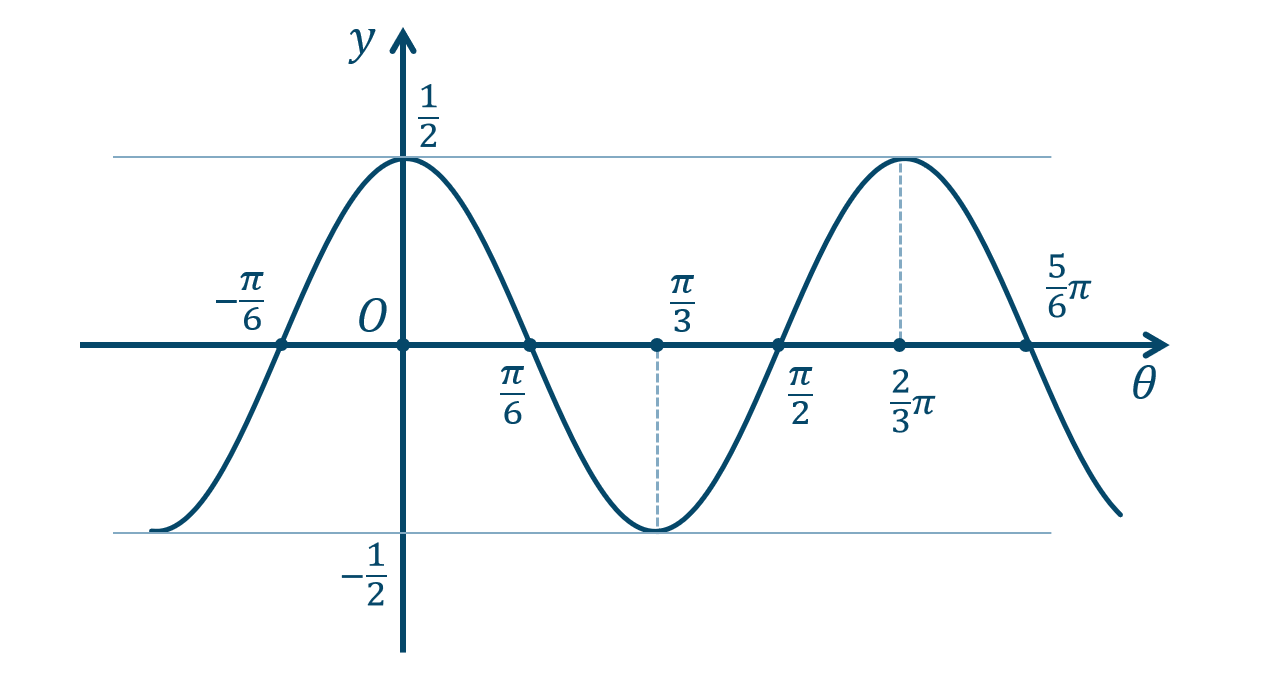
\({\small (1)}~\)

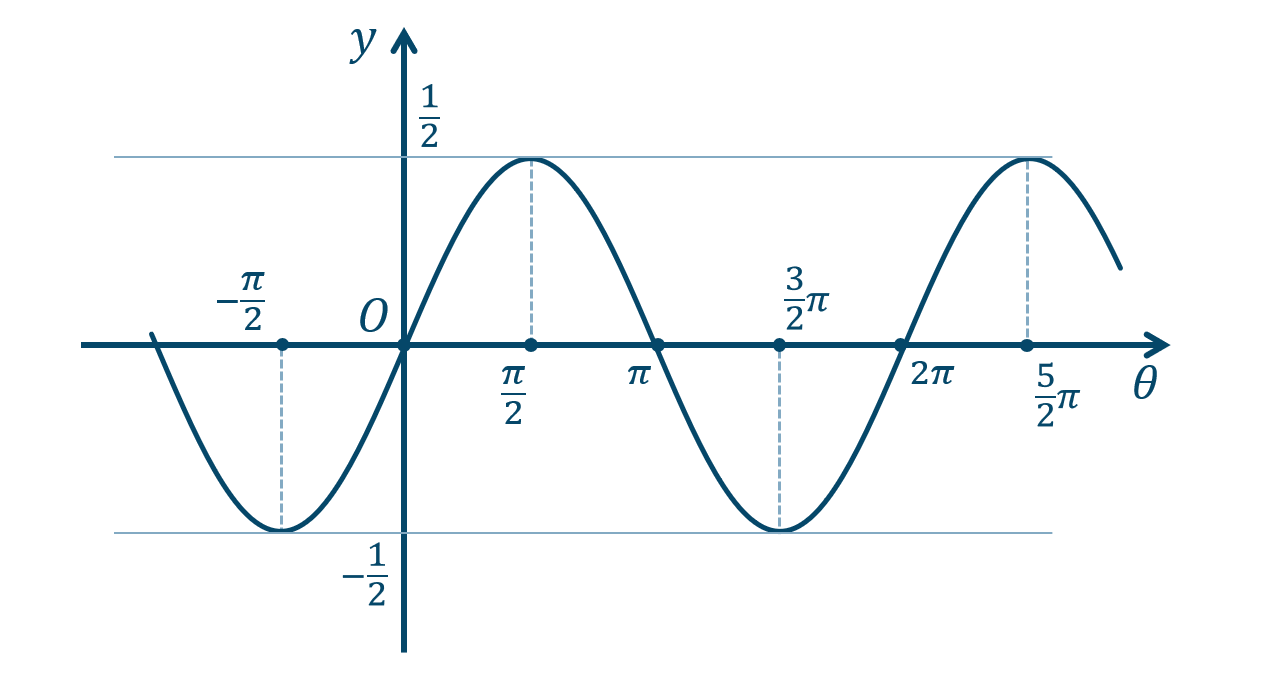
\({\small (2)}~\)

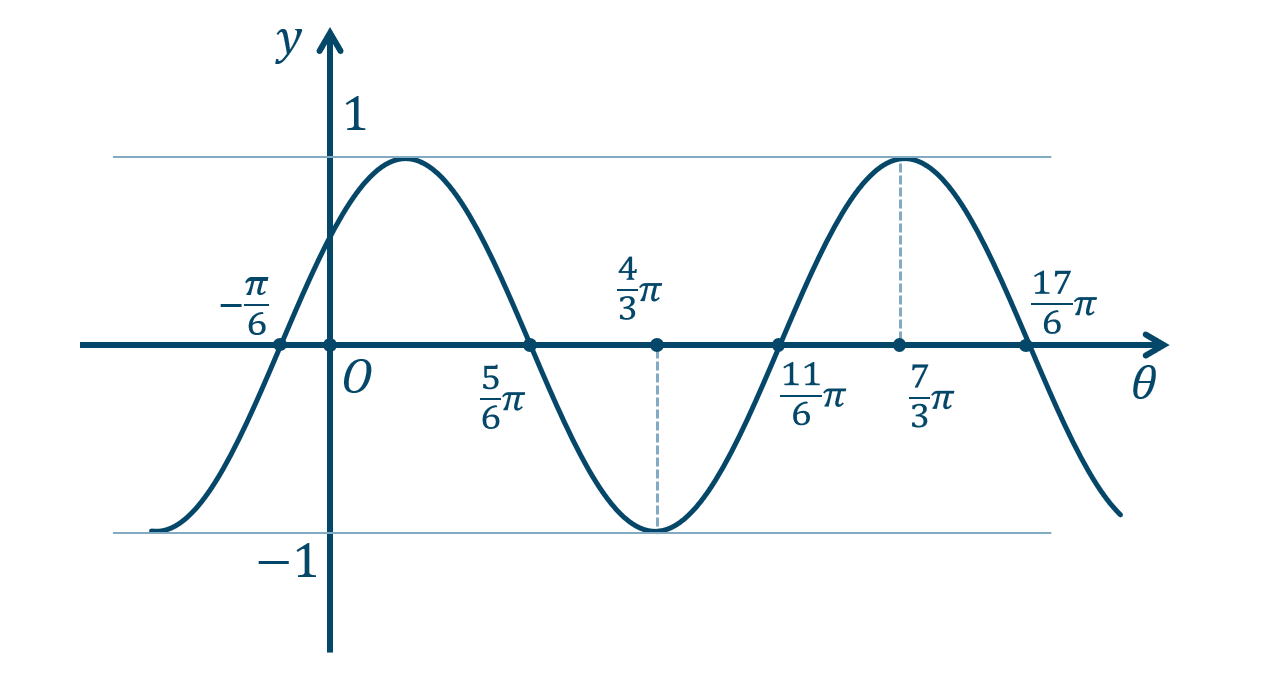
\({\small (3)}~\)

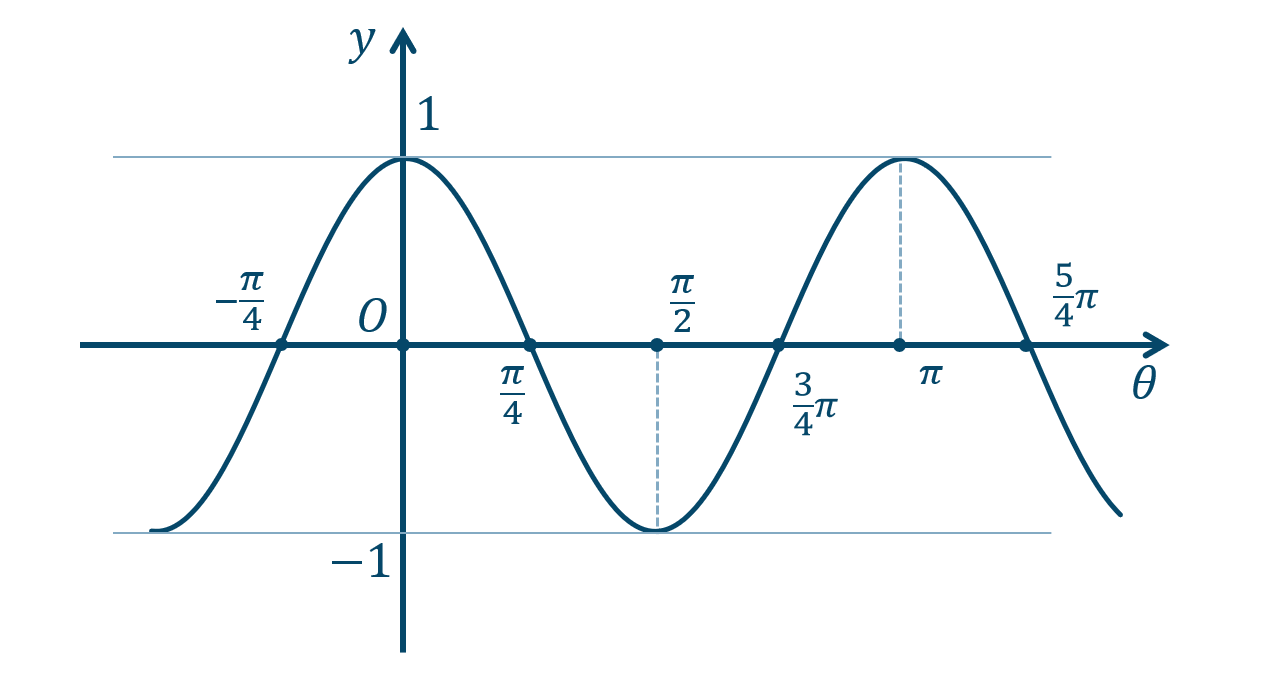
\({\small (4)}~\)

\({\small (1)}~\)

\({\small (2)}~\)

\({\small (3)}~\)
\({\small (4)}~\)

p.111 問2
\({\small (1)}~45^\circ+360^\circ\times n\) (\(n\) は整数)
\({\small (2)}~180^\circ+360^\circ\times n\) (\(n\) は整数)
\({\small (3)}~-30^\circ+360^\circ\times n\) (\(n\) は整数)
\({\small (1)}~45^\circ+360^\circ\times n\) (\(n\) は整数)
\({\small (2)}~180^\circ+360^\circ\times n\) (\(n\) は整数)
\({\small (3)}~-30^\circ+360^\circ\times n\) (\(n\) は整数)
p.111 問3
\({\small (1)}~60^\circ\) \({\small (2)}~10^\circ\)
\({\small (3)}~150^\circ\) \({\small (4)}~45^\circ\)
→ 動径と一般角
\({\small (1)}~60^\circ\) \({\small (2)}~10^\circ\)
\({\small (3)}~150^\circ\) \({\small (4)}~45^\circ\)
→ 動径と一般角
p.112 問4
\({\large \frac{3}{2}}\pi~,~{\large \frac{7}{4}}\pi~,~-{\large \frac{\pi}{3}}~,~-{\large \frac{5}{4}}\pi\)
\({\large \frac{3}{2}}\pi~,~{\large \frac{7}{4}}\pi~,~-{\large \frac{\pi}{3}}~,~-{\large \frac{5}{4}}\pi\)
p.113 問5
\(36^\circ~,~210^\circ~,~-330^\circ~,~-270^\circ\)
\(36^\circ~,~210^\circ~,~-330^\circ~,~-270^\circ\)
p.115 問7
\({\small (1)}~\)
\(\sin{{\large \frac{7}{6}}\pi}=-{\large \frac{1}{2}}~,~\cos{{\large \frac{7}{6}}\pi}=-{\large \frac{\sqrt{3}}{2}}\)
\(\tan{{\large \frac{7}{6}}\pi}={\large \frac{1}{\sqrt{3}}}\)
\({\small (2)}~\)
\(\sin{{\large \frac{9}{4}}\pi}={\large \frac{1}{\sqrt{2}}}~,~\cos{{\large \frac{9}{4}}\pi}={\large \frac{1}{\sqrt{2}}}\)
\(\tan{{\large \frac{9}{4}}\pi}=1\)
\({\small (3)}~\)
\(\sin{\left(-{\large \frac{\pi}{3}}\right)}=-{\large \frac{\sqrt{3}}{2}}~,~\cos{\left(-{\large \frac{\pi}{3}}\right)}={\large \frac{1}{2}}\)
\(\tan{\left(-{\large \frac{\pi}{3}}\right)}=-\sqrt{3}\)
\({\small (4)}~\)
\(\sin{(-3\pi)}=0~,~\cos{(-3\pi)}=-1\)
\(\tan{(-3\pi)}=0\)
→ 三角関数の値(単位円)
→ 【問題演習】三角関数の値(単位円)
\({\small (1)}~\)
\(\sin{{\large \frac{7}{6}}\pi}=-{\large \frac{1}{2}}~,~\cos{{\large \frac{7}{6}}\pi}=-{\large \frac{\sqrt{3}}{2}}\)
\(\tan{{\large \frac{7}{6}}\pi}={\large \frac{1}{\sqrt{3}}}\)
\({\small (2)}~\)
\(\sin{{\large \frac{9}{4}}\pi}={\large \frac{1}{\sqrt{2}}}~,~\cos{{\large \frac{9}{4}}\pi}={\large \frac{1}{\sqrt{2}}}\)
\(\tan{{\large \frac{9}{4}}\pi}=1\)
\({\small (3)}~\)
\(\sin{\left(-{\large \frac{\pi}{3}}\right)}=-{\large \frac{\sqrt{3}}{2}}~,~\cos{\left(-{\large \frac{\pi}{3}}\right)}={\large \frac{1}{2}}\)
\(\tan{\left(-{\large \frac{\pi}{3}}\right)}=-\sqrt{3}\)
\({\small (4)}~\)
\(\sin{(-3\pi)}=0~,~\cos{(-3\pi)}=-1\)
\(\tan{(-3\pi)}=0\)
→ 三角関数の値(単位円)
→ 【問題演習】三角関数の値(単位円)
p.115 問8
\({\small (1)}~\)第4象限
\({\small (2)}~\)第2象限
\({\small (1)}~\)第4象限
\({\small (2)}~\)第2象限
p.117 問9
\({\small (1)}~\)
\(\sin{\theta}=-{\large \frac{2\sqrt{2}}{3}}~,~\tan{\theta}=-2\sqrt{2}\)
\({\small (2)}~\)
\(\cos{\theta}=-{\large \frac{\sqrt{6}}{3}}~,~\tan{\theta}={\large \frac{\sqrt{2}}{2}}\)
\({\small (1)}~\)
\(\sin{\theta}=-{\large \frac{2\sqrt{2}}{3}}~,~\tan{\theta}=-2\sqrt{2}\)
\({\small (2)}~\)
\(\cos{\theta}=-{\large \frac{\sqrt{6}}{3}}~,~\tan{\theta}={\large \frac{\sqrt{2}}{2}}\)
p.117 問10
\(\cos{\theta}=-{\large \frac{2\sqrt{5}}{5}}~,~\sin{\theta}=-{\large \frac{\sqrt{5}}{5}}\)
→ 三角関数の相互関係の公式
\(\cos{\theta}=-{\large \frac{2\sqrt{5}}{5}}~,~\sin{\theta}=-{\large \frac{\sqrt{5}}{5}}\)
→ 三角関数の相互関係の公式
p.118 問12
[証明] (左辺)
\(={\large \frac{\cos{\theta}}{1+\sin{\theta}}}+\tan{\theta}\)
\(={\large \frac{\cos{\theta}}{1+\sin{\theta}}}\cdot{\large \frac{1-\sin{\theta}}{1-\sin{\theta}}}+\tan{\theta}\)
\(={\large \frac{\cos{\theta}(1-\sin{\theta})}{\cos^2{\theta}}}+{\large \frac{\sin{\theta}}{\cos{\theta}}}\)
\(={\large \frac{1-\sin{\theta}+\sin{\theta}}{\cos{\theta}}}\)
\(={\large \frac{1}{\cos{\theta}}}=\) (右辺)
したがって、
\({\large \frac{\cos{\theta}}{1+\sin{\theta}}}+\tan{\theta}={\large \frac{1}{\cos{\theta}}}\) [終]
→ 三角関数の等式の証明
[証明] (左辺)
\(={\large \frac{\cos{\theta}}{1+\sin{\theta}}}+\tan{\theta}\)
\(={\large \frac{\cos{\theta}}{1+\sin{\theta}}}\cdot{\large \frac{1-\sin{\theta}}{1-\sin{\theta}}}+\tan{\theta}\)
\(={\large \frac{\cos{\theta}(1-\sin{\theta})}{\cos^2{\theta}}}+{\large \frac{\sin{\theta}}{\cos{\theta}}}\)
\(={\large \frac{1-\sin{\theta}+\sin{\theta}}{\cos{\theta}}}\)
\(={\large \frac{1}{\cos{\theta}}}=\) (右辺)
したがって、
\({\large \frac{\cos{\theta}}{1+\sin{\theta}}}+\tan{\theta}={\large \frac{1}{\cos{\theta}}}\) [終]
→ 三角関数の等式の証明
p.119 問13
\(\sin{\left(-{\large \frac{\pi}{6}}\right)}=-{\large \frac{1}{2}}~,~\cos{\left(-{\large \frac{\pi}{6}}\right)}={\large \frac{\sqrt{3}}{2}}\)
\(\tan{\left(-{\large \frac{\pi}{6}}\right)}=-{\large \frac{1}{\sqrt{3}}}\)
\(\sin{\left(-{\large \frac{\pi}{6}}\right)}=-{\large \frac{1}{2}}~,~\cos{\left(-{\large \frac{\pi}{6}}\right)}={\large \frac{\sqrt{3}}{2}}\)
\(\tan{\left(-{\large \frac{\pi}{6}}\right)}=-{\large \frac{1}{\sqrt{3}}}\)
p.120 問14
\(\sin{{\large \frac{5}{4}}\pi}=-{\large \frac{1}{\sqrt{2}}}~,~\cos{{\large \frac{5}{4}}\pi}=-{\large \frac{1}{\sqrt{2}}}\)
\(\tan{{\large \frac{5}{4}}\pi}=1\)
→ 三角関数の性質①
\(\sin{{\large \frac{5}{4}}\pi}=-{\large \frac{1}{\sqrt{2}}}~,~\cos{{\large \frac{5}{4}}\pi}=-{\large \frac{1}{\sqrt{2}}}\)
\(\tan{{\large \frac{5}{4}}\pi}=1\)
→ 三角関数の性質①
p.121 問15
\({\small (1)}~{\large \frac{3}{8}}\pi\) \({\small (2)}~{\large \frac{\pi}{3}}\) \({\small (3)}~{\large \frac{\pi}{4}}\)
\({\small (4)}~{\large \frac{\pi}{6}}\) \({\small (5)}~{\large \frac{\pi}{8}}\) \({\small (6)}~{\large \frac{\pi}{4}}\)
→ 三角関数の性質②
\({\small (1)}~{\large \frac{3}{8}}\pi\) \({\small (2)}~{\large \frac{\pi}{3}}\) \({\small (3)}~{\large \frac{\pi}{4}}\)
\({\small (4)}~{\large \frac{\pi}{6}}\) \({\small (5)}~{\large \frac{\pi}{8}}\) \({\small (6)}~{\large \frac{\pi}{4}}\)
→ 三角関数の性質②
p.128 問21
\({\small (1)}~\theta={\large \frac{4}{3}}\pi~,~{\large \frac{5}{3}}\pi\)
\({\small (2)}~\theta={\large \frac{\pi}{4}}~,~{\large \frac{7}{4}}\pi\)
\({\small (3)}~\theta={\large \frac{3}{4}}\pi~,~{\large \frac{7}{4}}\pi\)
→ 三角関数を含む方程式①
→ 【問題演習】三角関数を含む方程式
\({\small (1)}~\theta={\large \frac{4}{3}}\pi~,~{\large \frac{5}{3}}\pi\)
\({\small (2)}~\theta={\large \frac{\pi}{4}}~,~{\large \frac{7}{4}}\pi\)
\({\small (3)}~\theta={\large \frac{3}{4}}\pi~,~{\large \frac{7}{4}}\pi\)
→ 三角関数を含む方程式①
→ 【問題演習】三角関数を含む方程式
p.129 問22
\({\small (1)}~\theta={\large \frac{\pi}{2}}~,~\pi\)
\({\small (2)}~\theta={\large \frac{\pi}{2}}~,~{\large \frac{5}{6}}\pi\)
→ 三角関数を含む方程式②(範囲変化)
\({\small (1)}~\theta={\large \frac{\pi}{2}}~,~\pi\)
\({\small (2)}~\theta={\large \frac{\pi}{2}}~,~{\large \frac{5}{6}}\pi\)
→ 三角関数を含む方程式②(範囲変化)
p.130 問23
\({\small (1)}~{\large \frac{2}{3}}\pi≦\theta≦{\large \frac{4}{3}}\pi\)
\({\small (2)}~0≦\theta<{\large \frac{\pi}{3}}~,~{\large \frac{5}{3}}\pi<\theta<2\pi\)
\({\small (3)}~0≦\theta≦{\large \frac{5}{4}}\pi~,~{\large \frac{7}{4}}\pi≦\theta<2\pi\)
\({\small (1)}~{\large \frac{2}{3}}\pi≦\theta≦{\large \frac{4}{3}}\pi\)
\({\small (2)}~0≦\theta<{\large \frac{\pi}{3}}~,~{\large \frac{5}{3}}\pi<\theta<2\pi\)
\({\small (3)}~0≦\theta≦{\large \frac{5}{4}}\pi~,~{\large \frac{7}{4}}\pi≦\theta<2\pi\)
p.131 問24
\({\small (1)}~-{\large \frac{\pi}{4}}<\theta<{\large \frac{\pi}{6}}\)
\({\small (2)}~-{\large \frac{\pi}{2}}<\theta≦{\large \frac{\pi}{3}}\)
→ 三角関数を含む不等式①
\({\small (1)}~-{\large \frac{\pi}{4}}<\theta<{\large \frac{\pi}{6}}\)
\({\small (2)}~-{\large \frac{\pi}{2}}<\theta≦{\large \frac{\pi}{3}}\)
→ 三角関数を含む不等式①
p.132 問1
Challenge
\({\small (1)}~\)
\(\theta={\large \frac{\pi}{3}}~,~{\large \frac{5}{3}}\pi\) で最大値 \({\large \frac{9}{4}}\)
\(\theta=\pi\) で最小値 \(0\)
\({\small (2)}~\)
\(\theta={\large \frac{\pi}{6}}~,~{\large \frac{5}{6}}\pi\) で最大値 \({\large \frac{5}{4}}\)
\(\theta={\large \frac{3}{2}}\pi\) で最小値 \(-1\)
→ 三角関数を含む2次関数
Challenge
\({\small (1)}~\)
\(\theta={\large \frac{\pi}{3}}~,~{\large \frac{5}{3}}\pi\) で最大値 \({\large \frac{9}{4}}\)
\(\theta=\pi\) で最小値 \(0\)
\({\small (2)}~\)
\(\theta={\large \frac{\pi}{6}}~,~{\large \frac{5}{6}}\pi\) で最大値 \({\large \frac{5}{4}}\)
\(\theta={\large \frac{3}{2}}\pi\) で最小値 \(-1\)
→ 三角関数を含む2次関数
Training