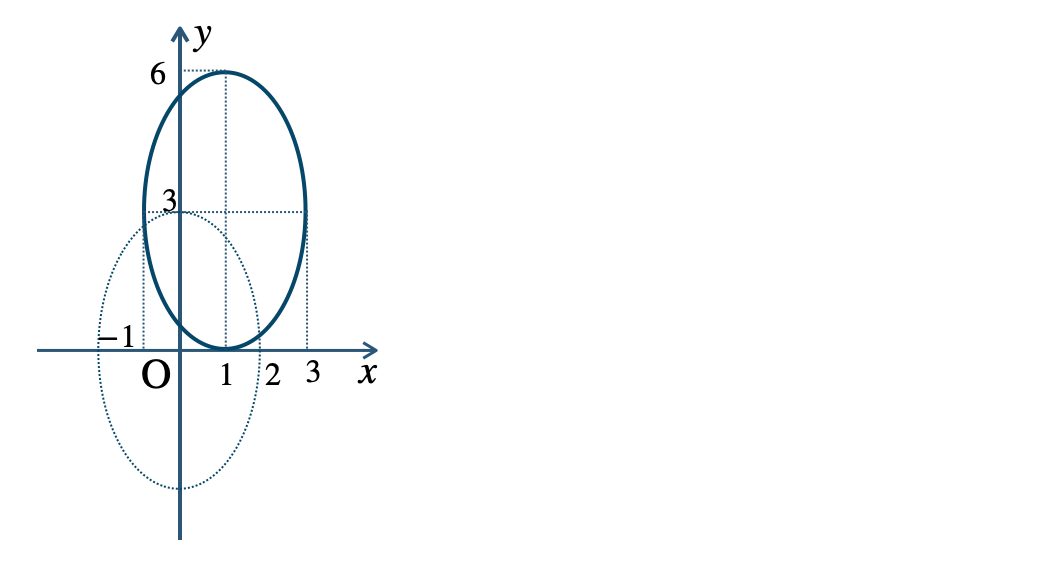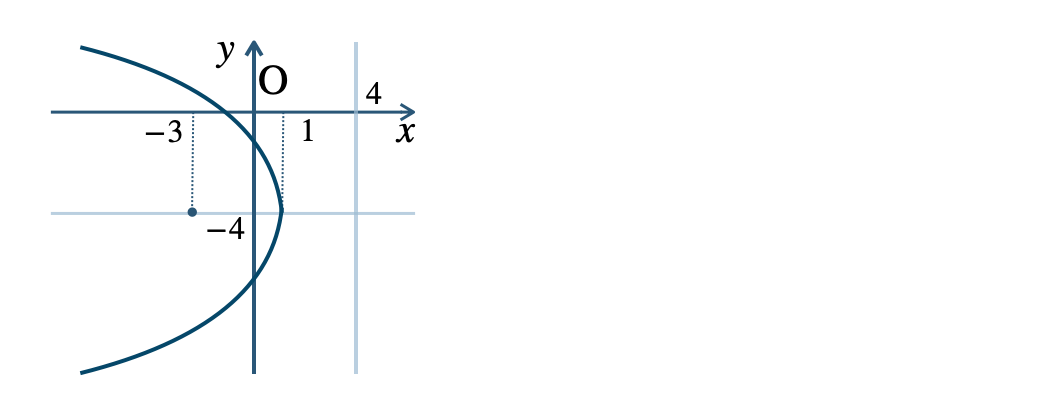文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
第１章 平面のベクトル
第２章 空間のベクトル
第３章 複素数平面
第４章 式と曲線
第４章 式と曲線
第１節 ２次曲線
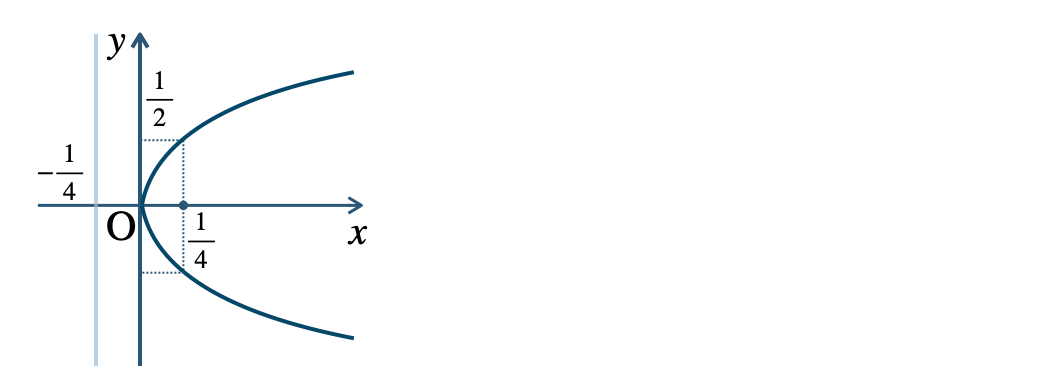
p.117 練習1\({\small (1)}~\)焦点 \(\left(\frac{\,1\,}{\,4\,}~,~0 \right)\)、準線 \(x=-{\large \frac{\,1\,}{\,4\,}}\)
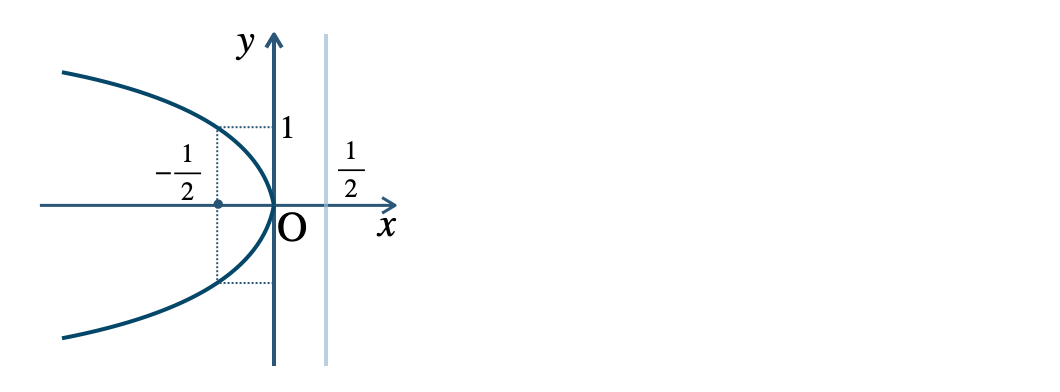
\({\small (2)}~\)焦点 \(\left(-\frac{\,1\,}{\,2\,}~,~0 \right)\)、準線 \(x={\large \frac{\,1\,}{\,2\,}}\)
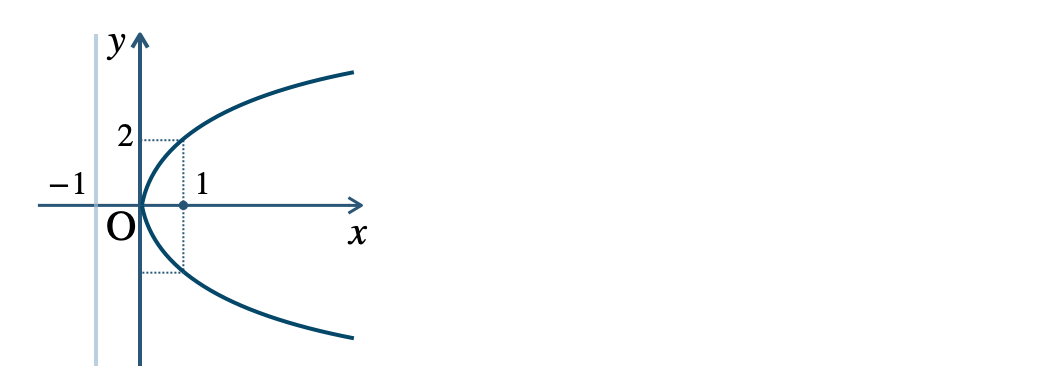
p.117 練習2$${\small (1)}~y^2=4x$$
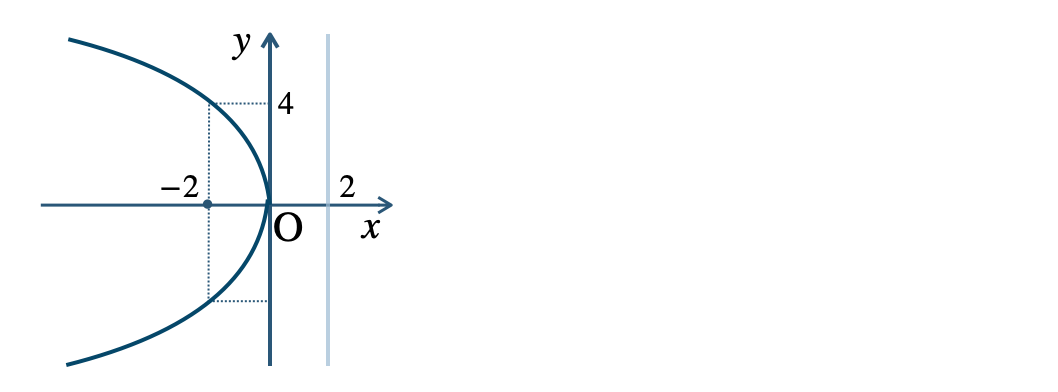
$${\small (2)}~y^2=-8x$$
p.117 練習3 焦点 \(\left(0~,~\frac{\,1\,}{\,4\,}\right)\)、準線 \(y=-{\large \frac{\,1\,}{\,4\,}}\)
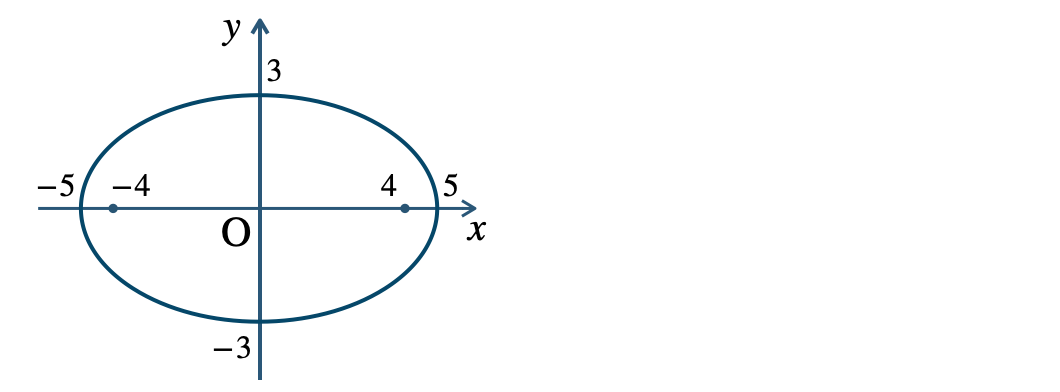
p.120 練習4\({\small (1)}~\)長軸 \(10\)、短軸 \(6\)
焦点 \((4~,~0)~,~(-4~,~0)\)
頂点 \((5~,~0)~,~(-5~,~0)~,~(0~,~3)~,~(0~,~-3)\)
焦点 \((4~,~0)~,~(-4~,~0)\)
頂点 \((5~,~0)~,~(-5~,~0)~,~(0~,~3)~,~(0~,~-3)\)
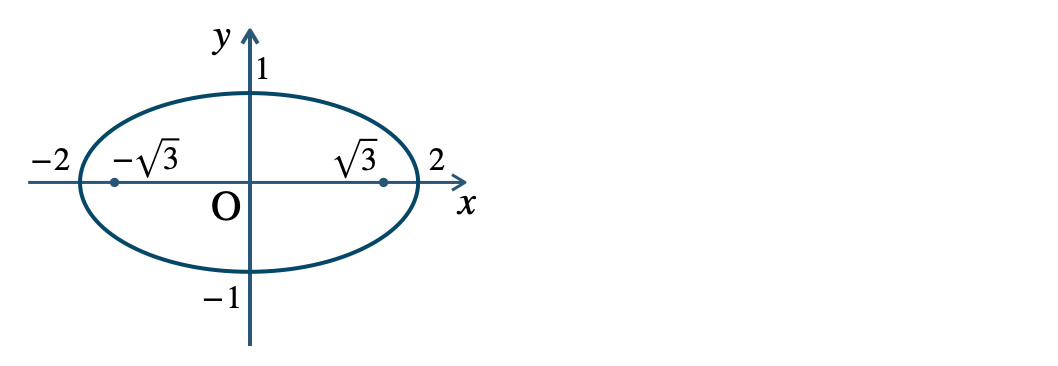
\({\small (2)}~\)長軸 \(4\)、短軸 \(2\)
焦点 \((\sqrt{3}~,~0)~,~(-\sqrt{3}~,~0)\)
頂点 \((2~,~0)~,~(-2~,~0)~,~(0~,~1)~,~(0~,~-1)\)
p.120 問1$$~~~\frac{\,x^2\,}{\,25\,}+\frac{\,y^2\,}{\,16\,}=1$$
p.120 練習5$$~~~\frac{\,x^2\,}{\,9\,}+\frac{\,y^2\,}{\,3\,}=1$$
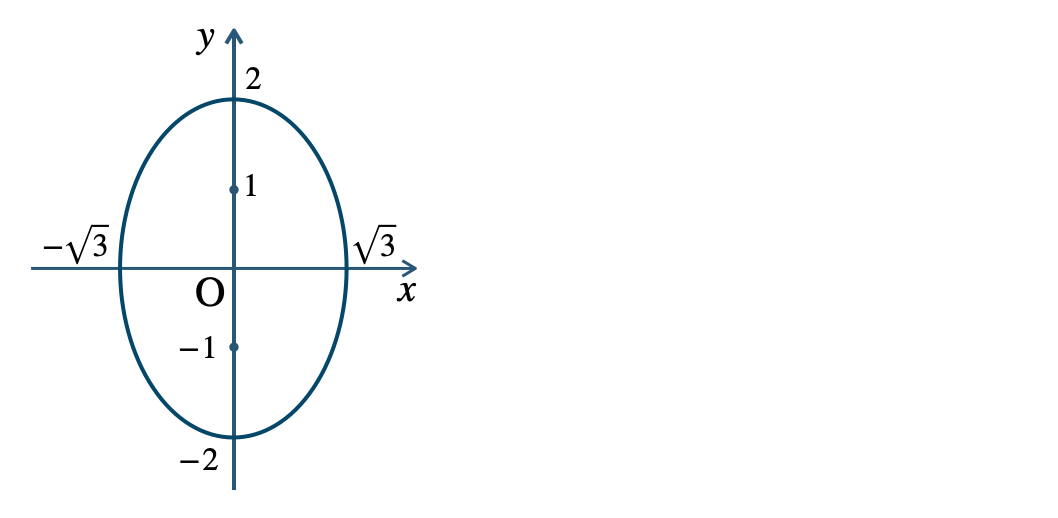
p.121 練習6\({\small (1)}~\)長軸 \(4\)、短軸 \(2\sqrt{3}\)
焦点 \((0~,~1)~,~(0~,~-1)\)
焦点 \((0~,~1)~,~(0~,~-1)\)
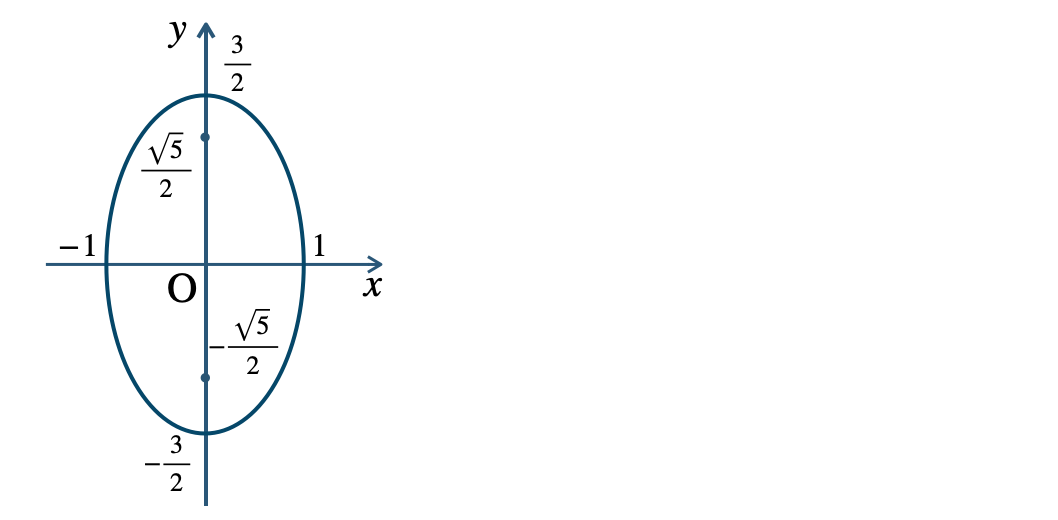
\({\small (2)}~\)長軸 \(3\)、短軸 \(2\)
焦点 \(\left(0~,~{\large \frac{\,\sqrt{5}\,}{\,2\,}}\right)~,~\left(0~,~-{\large \frac{\,\sqrt{5}\,}{\,2\,}}\right)\)
p.122 問2$$~~~\frac{\,x^2\,}{\,36\,}+\frac{\,y^2\,}{\,9\,}=1$$
p.122 練習7$${\small (1)}~\frac{\,x^2\,}{\,16\,}+\frac{\,y^2\,}{\,9\,}=1$$$${\small (2)}~\frac{\,x^2\,}{\,36\,}+\frac{\,y^2\,}{\,16\,}=1$$
p.123 練習8$$~~~\frac{\,x^2\,}{\,9\,}+\frac{\,y^2\,}{\,16\,}=1$$
p.123 練習9$$~~~\frac{\,x^2\,}{\,25\,}+\frac{\,y^2\,}{\,100\,}=1$$
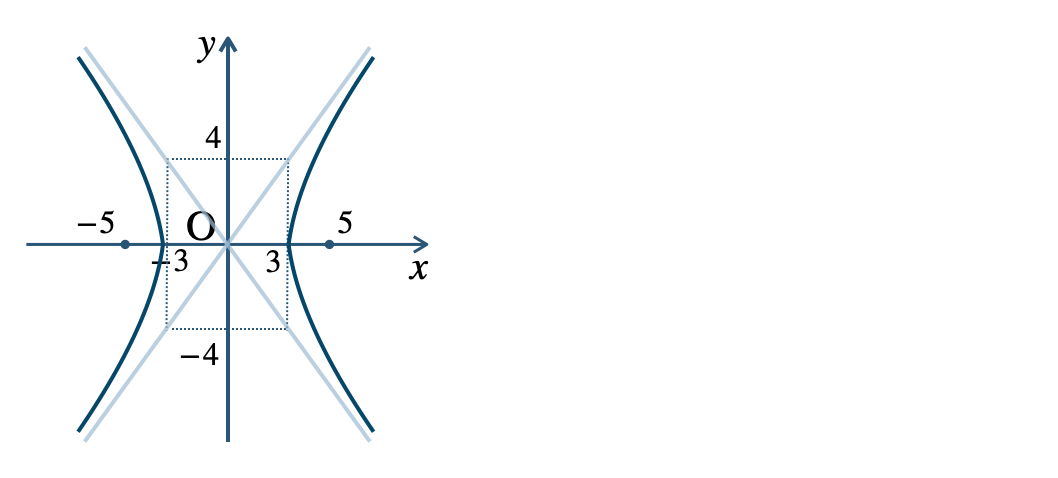
p.126 練習10\({\small (1)}~\)頂点 \((3~,~0)~,~(-3~,~0)\)
焦点 \((5~,~0)~,~(-5~,~0)\)
漸近線$$~~~\frac{\,x\,}{\,3\,}-\frac{\,y\,}{\,4\,}=0~,~\frac{\,x\,}{\,3\,}+\frac{\,y\,}{\,4\,}=0$$
焦点 \((5~,~0)~,~(-5~,~0)\)
漸近線$$~~~\frac{\,x\,}{\,3\,}-\frac{\,y\,}{\,4\,}=0~,~\frac{\,x\,}{\,3\,}+\frac{\,y\,}{\,4\,}=0$$
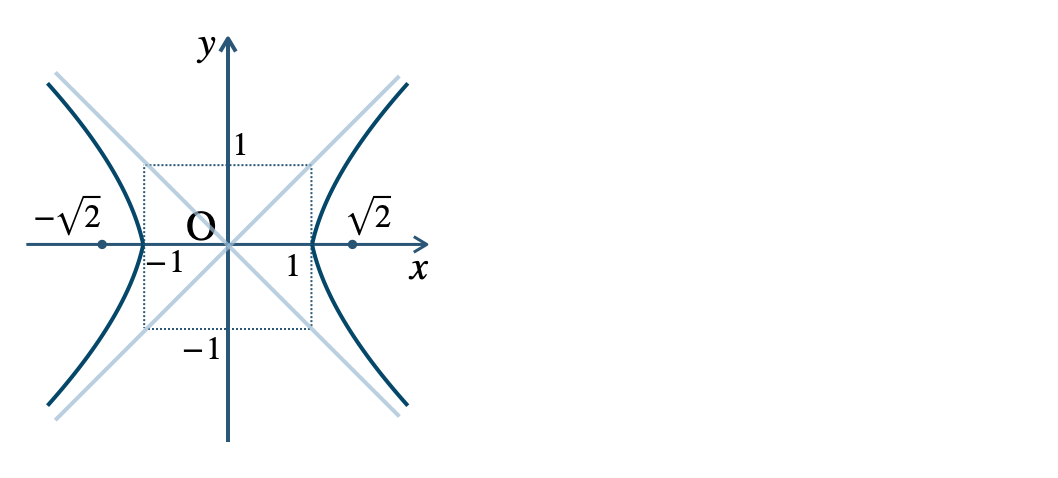
\({\small (2)}~\)頂点 \((1~,~0)~,~(-1~,~0)\)
焦点 \((\sqrt{2}~,~0)~,~(-\sqrt{2}~,~0)\)
漸近線$$~~~x-y=0~,~x+y=0$$
p.126 問3$$~~~\frac{\,x^2\,}{\,16\,}-\frac{\,y^2\,}{\,9\,}=1$$
p.126 練習11$$~~~\frac{\,x^2\,}{\,4\,}-\frac{\,y^2\,}{\,5\,}=1$$
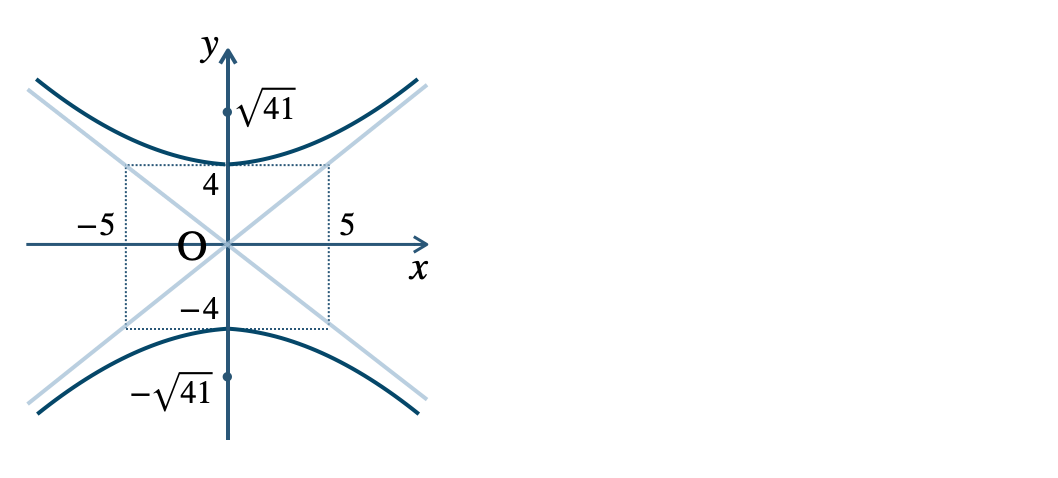
p.127 練習12\({\small (1)}~\)頂点 \((0~,~4)~,~(0~,~-4)\)
焦点 \((0~,~\sqrt{41})~,~(0~,~-\sqrt{41})\)
漸近線$$~~~\frac{\,x\,}{\,5\,}-\frac{\,y\,}{\,4\,}=0~,~\frac{\,x\,}{\,5\,}+\frac{\,y\,}{\,4\,}=0$$
焦点 \((0~,~\sqrt{41})~,~(0~,~-\sqrt{41})\)
漸近線$$~~~\frac{\,x\,}{\,5\,}-\frac{\,y\,}{\,4\,}=0~,~\frac{\,x\,}{\,5\,}+\frac{\,y\,}{\,4\,}=0$$
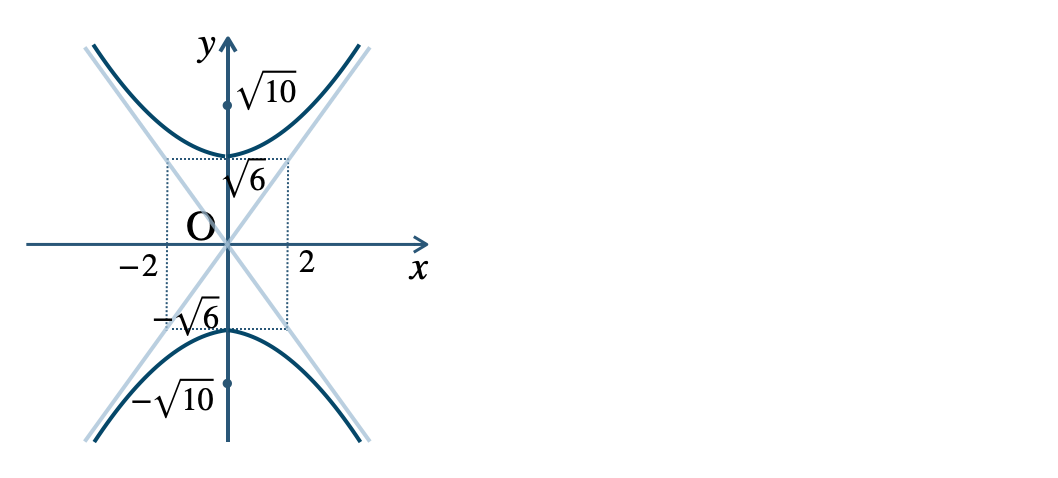
\({\small (2)}~\)頂点 \((0~,~\sqrt{6})~,~(0~,~-\sqrt{6})\)
焦点 \((0~,~\sqrt{10})~,~(0~,~-\sqrt{10})\)
漸近線$$~~~\frac{\,x\,}{\,2\,}-\frac{\,y\,}{\,\sqrt{6}\,}=0~,~\frac{\,x\,}{\,2\,}+\frac{\,y\,}{\,\sqrt{6}\,}=0$$
p.128 練習13$${\small (1)}~\frac{\,x^2\,}{\,2\,}-\frac{\,y^2\,}{\,2\,}=1$$$${\small (2)}~\frac{\,x^2\,}{\,4\,}-\frac{\,y^2\,}{\,4\,}=-1$$
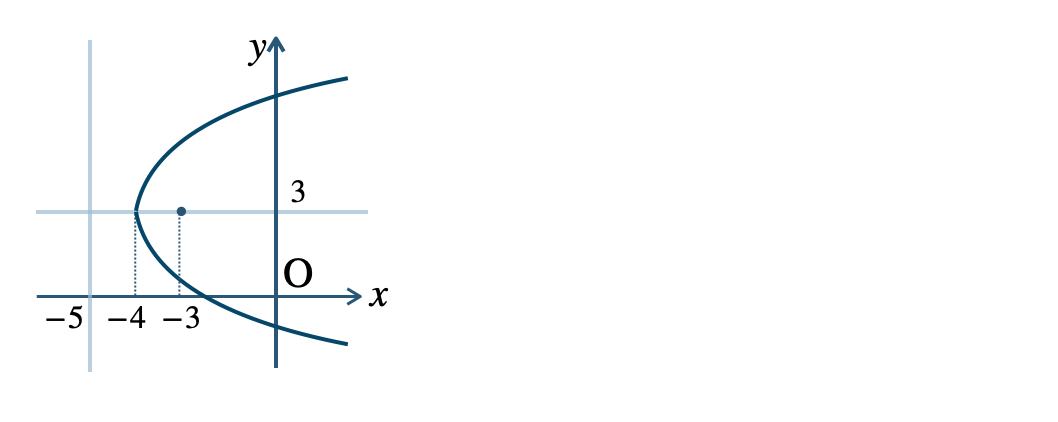
p.130 問4$$~~~(y-2)^2=8(x+1)$$ 焦点 \((1~,~2)\)、準線 \(x=-3\)
p.130 練習14$${\small (1)}~\frac{\,(x+2)^2\,}{\,4\,}+(y-3)^2=1$$ 焦点 \((\sqrt{3}-2~,~3)~,~(-\sqrt{3}-2~,~3)\)$${\small (2)}~\frac{\,(x+2)^2\,}{\,4\,}-\frac{\,(y-3)^2\,}{\,9\,}=1$$ 焦点 \((\sqrt{13}-2~,~3)~,~(-\sqrt{13}-2~,~3)\)$${\small (3)}~(y-3)^2=4(x+2)$$ 焦点 \((-1~,~3)\)
p.131 練習15\({\small (1)}~\)楕円 \({\large \frac{\,x^2\,}{\,4\,}}+{\large \frac{\,y^2\,}{\,9\,}}=1\) を \(x\) 軸方向に \(1\)、\(y\) 軸方向に \(3\) だけ平行移動させた楕円
\({\small (2)}~\)双曲線 \({\large \frac{\,x^2\,}{\,4\,}}-y^2=1\) を \(x\) 軸方向に \(-1\)、\(y\) 軸方向に \(-2\) だけ平行移動させた双曲線
p.131 問5[証明]$$\begin{eqnarray}~~~y^2-6y-4x-7&=&0\\[2pt]~~~y^2-6y+9&=&4x+16\\[2pt]~~~(y-3)^2&=&4(x+4)\end{eqnarray}$$これより、放物線 \(y^2=4x\) を \(x\) 軸方向に \(-4\)、\(y\) 軸方向に \(3\) だけ平行移動させた放物線 [終]
頂点 \((-4~,~3)\)、焦点 \((-3~,~3)\)、準線\(x=-5\)
p.131 練習16放物線 \(y^2=-16x\) を \(x\) 軸方向に \(1\)、\(y\) 軸方向に \(-4\) だけ平行移動させた放物線
p.133 練習17$${\small (1)}~(0~,~-3)~,~\left(\frac{\,24\,}{\,13\,}~,~-\frac{\,15\,}{\,13\,} \right)$$$${\small (2)}~\left(\frac{\,2\,}{\,\sqrt{3}\,}~,~\frac{\,1\,}{\,\sqrt{3}\,} \right)~,~\left(-\frac{\,2\,}{\,\sqrt{3}\,}~,~-\frac{\,1\,}{\,\sqrt{3}\,} \right)$$$${\small (3)}~(2~,~4)$$
p.134 練習18\({\small (1)}~\)
\(k< -2~,~2< k\) のとき、２個
\(k=\pm 2\) のとき、１個
\(-2< k< 2\) のとき、０個
\({\small (2)}~\)
\(-1 < k < 1\) のとき、２個
\(k≦-1~,~1≦k\) のとき、０個
\(k< -2~,~2< k\) のとき、２個
\(k=\pm 2\) のとき、１個
\(-2< k< 2\) のとき、０個
\({\small (2)}~\)
\(-1 < k < 1\) のとき、２個
\(k≦-1~,~1≦k\) のとき、０個
p.135 練習19$$~~~\left( \frac{\,1\,}{\,4\,}~,~\frac{\,1\,}{\,2\,} \right)$$
p.136 練習20$$~~~y=\frac{\,1\,}{\,2\,}x+2~,~(4~,~4)$$$$~~~y=-\frac{\,1\,}{\,2\,}x-2~,~(4~,~-4)$$
p.137 練習21[証明] 点 \({\rm P~,~Q}\) は放物線 \(y^2=4x\) 上の点より、$$\begin{eqnarray} \left\{\begin{array}{l}
y_1^2=4x_1 \\ y_2^2=4x_2
\end{array}\right.\end{eqnarray}$$ここで、\(y_1=y_2\) のとき \(x_1=x_2\) となり２点が一致するので、\(y_1 \neq y_2\)
また、それぞれの接線の方程式は、$$\begin{eqnarray} \left\{\begin{array}{l}
y_1y=2(x+x_1) \\ y_2y=2(x+x_2)
\end{array}\right.\end{eqnarray}$$これらを連立して、上の式を代入すると、$$\begin{eqnarray}~~~(y_1-y_2)y&=&2(x_1-x_2)
\\[3pt]~~~y&=&2\frac{\,x_1-x_2\,}{\,y_1-y_2\,}
\\[3pt]~~~y&=&2\cdot \frac{\,1\,}{\,4\,} \cdot \frac{\,y_1^2-y_2^2\,}{\,y_1-y_2\,}
\\[3pt]~~~&=&\frac{\,y_1+y_2\,}{\,2\,}
\end{eqnarray}$$これより、点 \({\rm R}\) の \(y\) 座標が \({\large \frac{\,y_1+y_2\,}{\,2\,}}\)
また、線分 \({\rm PQ}\) の中点 \({\rm M}\) の \(y\) 座標も \({\large \frac{\,y_1+y_2\,}{\,2\,}}\)
したがって、点 \({\rm R~,~M}\) の \(y\) 座標が一致するので、直線 \({\rm RM}\) は \(x\) 軸に平行である [終]
y_1^2=4x_1 \\ y_2^2=4x_2
\end{array}\right.\end{eqnarray}$$ここで、\(y_1=y_2\) のとき \(x_1=x_2\) となり２点が一致するので、\(y_1 \neq y_2\)
また、それぞれの接線の方程式は、$$\begin{eqnarray} \left\{\begin{array}{l}
y_1y=2(x+x_1) \\ y_2y=2(x+x_2)
\end{array}\right.\end{eqnarray}$$これらを連立して、上の式を代入すると、$$\begin{eqnarray}~~~(y_1-y_2)y&=&2(x_1-x_2)
\\[3pt]~~~y&=&2\frac{\,x_1-x_2\,}{\,y_1-y_2\,}
\\[3pt]~~~y&=&2\cdot \frac{\,1\,}{\,4\,} \cdot \frac{\,y_1^2-y_2^2\,}{\,y_1-y_2\,}
\\[3pt]~~~&=&\frac{\,y_1+y_2\,}{\,2\,}
\end{eqnarray}$$これより、点 \({\rm R}\) の \(y\) 座標が \({\large \frac{\,y_1+y_2\,}{\,2\,}}\)
また、線分 \({\rm PQ}\) の中点 \({\rm M}\) の \(y\) 座標も \({\large \frac{\,y_1+y_2\,}{\,2\,}}\)
したがって、点 \({\rm R~,~M}\) の \(y\) 座標が一致するので、直線 \({\rm RM}\) は \(x\) 軸に平行である [終]
p.138 研究 練習1$${\small (1)}~2\sqrt{3}x+3\sqrt{2}y=12$$$${\small (2)}~3x+2y=5$$
p.141 問6[証明] 点 \({\rm P}\) の座標を \((x~,~y)\) とすると、$$~~~{\rm PF}=\sqrt{(x-4)^2+y^2}$$また、点 \({\rm P}\) から直線 \(x=1\) に下ろした点を \({\rm H}\) とすると、$$~~~{\rm PH}=|x-1|$$\({\rm PF:PH}=2:1\) であるので、$$\begin{eqnarray}~~~\sqrt{(x-4)^2+y^2}&=&2|x-1|
\\[2pt]~~~(x-4)^2+y^2&=&4(x-1)^2
\\[2pt]~~~3x^2-y^2&=&12
\\[3pt]~~~\frac{\,x^2\,}{\,4\,}-\frac{\,y^2\,}{\,12\,}&=&1
\end{eqnarray}$$よって、条件を満たす点 \({\rm P}\) は双曲線上にある
逆に、双曲線上の任意の点は条件を満たす
したがって、点 \({\rm P}\) の軌跡は \({\large \frac{\,x^2\,}{\,4\,}}-{\large \frac{\,y^2\,}{\,12\,}}=1\) [終]
[証明] 双曲線において、\(a=2~,~b=2\sqrt{3}\) となるので、$$~~~\sqrt{a^2+a^2}=\sqrt{4+12}=4$$したがって、焦点の１つが \((4~,~0)\) [終]
\\[2pt]~~~(x-4)^2+y^2&=&4(x-1)^2
\\[2pt]~~~3x^2-y^2&=&12
\\[3pt]~~~\frac{\,x^2\,}{\,4\,}-\frac{\,y^2\,}{\,12\,}&=&1
\end{eqnarray}$$よって、条件を満たす点 \({\rm P}\) は双曲線上にある
逆に、双曲線上の任意の点は条件を満たす
したがって、点 \({\rm P}\) の軌跡は \({\large \frac{\,x^2\,}{\,4\,}}-{\large \frac{\,y^2\,}{\,12\,}}=1\) [終]
[証明] 双曲線において、\(a=2~,~b=2\sqrt{3}\) となるので、$$~~~\sqrt{a^2+a^2}=\sqrt{4+12}=4$$したがって、焦点の１つが \((4~,~0)\) [終]
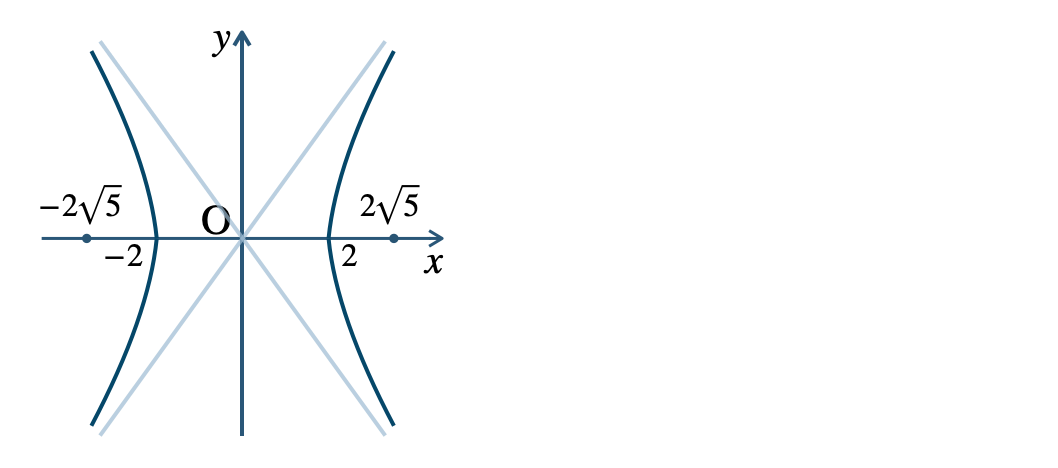
p.141 練習22$$~~~x^2-\frac{\,y^2\,}{\,8\,}=1$$
第２節 媒介変数表示と極座標
p.143 練習23\({\small (1)}~\)放物線 \(y=x^2+5x+6\)
\({\small (2)}~\)放物線 \(y=x^2+1\) の \(x≧0\)
\({\small (2)}~\)放物線 \(y=x^2+1\) の \(x≧0\)
p.144 練習24 放物線 \(y=x^2+x\)
p.144 練習25$${\small (1)}~x=t^2~,~y=2t$$$${\small (2)}~x=-2t^2~,~y=-4t$$
p.145 練習26$$~~~x=\frac{\,4p\,}{\,t^2\,}~,~y=\frac{\,4p\,}{\,t\,}$$
p.146 練習27$${\small (1)}~x=\cos{\theta}~,~y=\sin{\theta}$$$${\small (2)}~x=\sqrt{3}\cos{\theta}~,~y=\sqrt{3}\sin{\theta}$$
p.146 問7$$~~~x=3\cos{\theta}~,~y=2\sin{\theta}$$
p.146 練習28$${\small (1)}~x=4\cos{\theta}~,~y=3\sin{\theta}$$$${\small (2)}~x=2\cos{\theta}~,~y=5\sin{\theta}$$
p.147 練習29$${\small (1)}~x=\frac{\,3\,}{\,\cos{\theta}\,}~,~y=2\tan{\theta}$$$${\small (2)}~x=\frac{\,2\,}{\,\cos{\theta}\,}~,~y=\sqrt{3}\tan{\theta}$$
p.148 練習30\({\small (1)}~\)楕円$$~~~\frac{\,(x+3)^2\,}{\,4\,}+\frac{\,(y-2)^2\,}{\,9\,}=1$$\({\small (2)}~\)双曲線$$~~~\frac{\,(x-3)^2\,}{\,9\,}-\frac{\,(y-1)^2\,}{\,4\,}=1$$
p.149 練習31$${\small (1)}~\left( \frac{\,2\,}{\,3\,}\pi-\sqrt{3}~,~1 \right)$$$${\small (2)}~(2\pi~,~4)$$$${\small (3)}~(3\pi+2~,~2)$$$${\small (4)}~(4\pi~,~0)$$
p.151 練習32
p.153 練習33$${\small (1)}~(2\sqrt{3}~,~2)$$$${\small (2)}~(-1~,~-\sqrt{3})$$$${\small (3)}~\left( \frac{\,3\,}{\,\sqrt{2}\,}~,~-\frac{\,3\,}{\,\sqrt{2}\,} \right)$$
p.153 練習34$${\small (1)}~\left(\sqrt{2}~,~\frac{\,\pi\,}{\,4\,} \right)$$$${\small (2)}~\left(3~,~\pi \right)$$$${\small (3)}~\left(2~,~\frac{\,7\,}{\,6\,}\pi \right)$$
p.155 練習35\({\small (1)}~\)
\({\small (2)}~\)
\({\small (3)}~\)
p.155 練習36\({\small (1)}~\)
\({\small (2)}~\)
p.156 練習37$${\small (1)}~xy=1$$$${\small (2)}~x^2+y^2-2y=0$$$${\small (3)}~y=x+1$$
p.157 練習38$${\small (1)}~r^2=\frac{\,4\,}{\,2-\cos^2{\theta}\,}$$$${\small (2)}~r=2\cos{\theta}$$
p.157 練習39$$~~~r=\frac{\,2\,}{\,1-\sin{\theta}\,}$$
p.158 問8$$~~~3x^2-8x-y^2=-4$$
p.158 練習40$${\small (1)}~y^2+8x-16=0$$$${\small (2)}~3x^2+2x+4y^2=1$$
問題
p.162 問題 9[証明] 円の中心を \({\rm C}(r_1~,~\theta_1)\)、円上の点を \({\rm P}(r~,~\theta)\) とすると、
３点 \({\rm O~,~C~,~P}\) で三角形ができるとき、\(\angle{\rm POC}=|\theta-\theta_1|\) で余弦定理より、$$~~~r^2+r_1^2-2rr_1\cos{(\theta-\theta_1)}=a^2$$これは点 \({\rm C}\) と \({\rm O}\) が一致するときや、点 \({\rm P}\) が直線 \({\rm OC}\) 上にあるときも成り立つ
逆に、点 \({\rm P}\) はこの円上の点である
したがって、円の極方程式は、$$~~~r^2+r_1^2-2rr_1\cos{(\theta-\theta_1)}=a^2$$[終]
３点 \({\rm O~,~C~,~P}\) で三角形ができるとき、\(\angle{\rm POC}=|\theta-\theta_1|\) で余弦定理より、$$~~~r^2+r_1^2-2rr_1\cos{(\theta-\theta_1)}=a^2$$これは点 \({\rm C}\) と \({\rm O}\) が一致するときや、点 \({\rm P}\) が直線 \({\rm OC}\) 上にあるときも成り立つ
逆に、点 \({\rm P}\) はこの円上の点である
したがって、円の極方程式は、$$~~~r^2+r_1^2-2rr_1\cos{(\theta-\theta_1)}=a^2$$[終]
p.162 問題 10$$~~~(x-2)^2-\frac{\,y^2\,}{\,3\,}=1$$
演習問題
p.163 演習問題Ａ 3$$~~~\frac{\,x^2\,}{\,4\,}-\frac{\,y^2\,}{\,16\,}=1$$
p.163 演習問題Ｂ 6\({\small (1)}~\)[証明] 点 \({\rm P}(x~,~y)\) とすると、
\({\rm PA\cdot PB}=a^2\) であるので、$$\scriptsize \begin{eqnarray}~~~\sqrt{(x+a)^2+y^2}\sqrt{(x-a)^2+y^2}&=&a^2
\\[2pt]~~~\{(x+a)^2+^2\}\{(x-a)^2+^2\}&=&a^4
\\[2pt]~~~\{x^2+y^2+a^2+2ax\}\{x^2+y^2+a^2-2ax\}&=&a^4
\\[2pt]~~~(x^2+y^2+a^2)^2-4a^2x^2&=&a^4
\\[2pt]~~~(x^2+y^2)^2+2a^2(x^2+y^2)+a^4-4a^2x^2&=&a^4
\end{eqnarray}$$これより、$$\small \begin{eqnarray}~~~(x^2+y^2)^2&=&4a^2x^2-2a^2(x^2+y^2)
\\[2pt]~~~(x^2+y^2)^2&=&2a^2(x^2-y^2)
\end{eqnarray}$$[終]
\({\rm PA\cdot PB}=a^2\) であるので、$$\scriptsize \begin{eqnarray}~~~\sqrt{(x+a)^2+y^2}\sqrt{(x-a)^2+y^2}&=&a^2
\\[2pt]~~~\{(x+a)^2+^2\}\{(x-a)^2+^2\}&=&a^4
\\[2pt]~~~\{x^2+y^2+a^2+2ax\}\{x^2+y^2+a^2-2ax\}&=&a^4
\\[2pt]~~~(x^2+y^2+a^2)^2-4a^2x^2&=&a^4
\\[2pt]~~~(x^2+y^2)^2+2a^2(x^2+y^2)+a^4-4a^2x^2&=&a^4
\end{eqnarray}$$これより、$$\small \begin{eqnarray}~~~(x^2+y^2)^2&=&4a^2x^2-2a^2(x^2+y^2)
\\[2pt]~~~(x^2+y^2)^2&=&2a^2(x^2-y^2)
\end{eqnarray}$$[終]
