【教科書レベルの問題一覧と解答】数学Ⅲ｜２次曲線

このページは「高校数学Ⅲ：２次曲線」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう！
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。

【問題一覧】数学Ⅲ：２次曲線

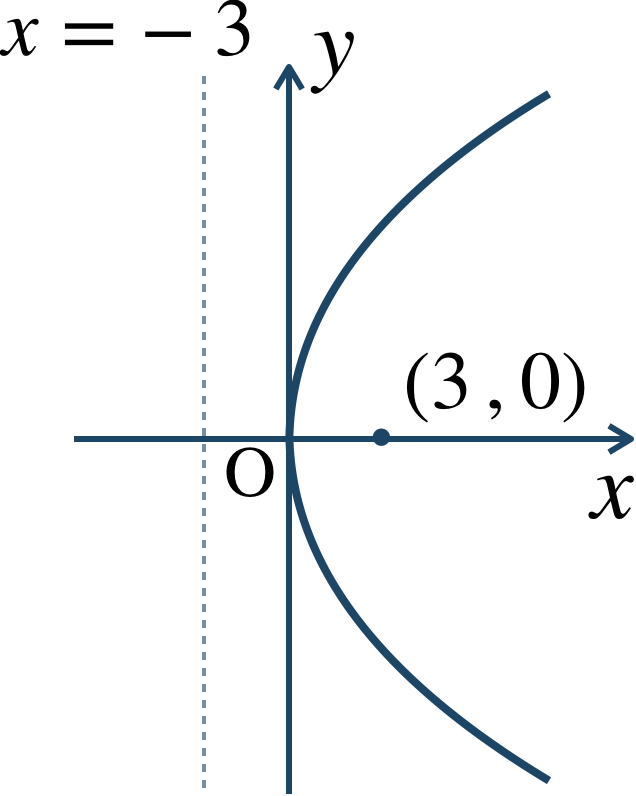
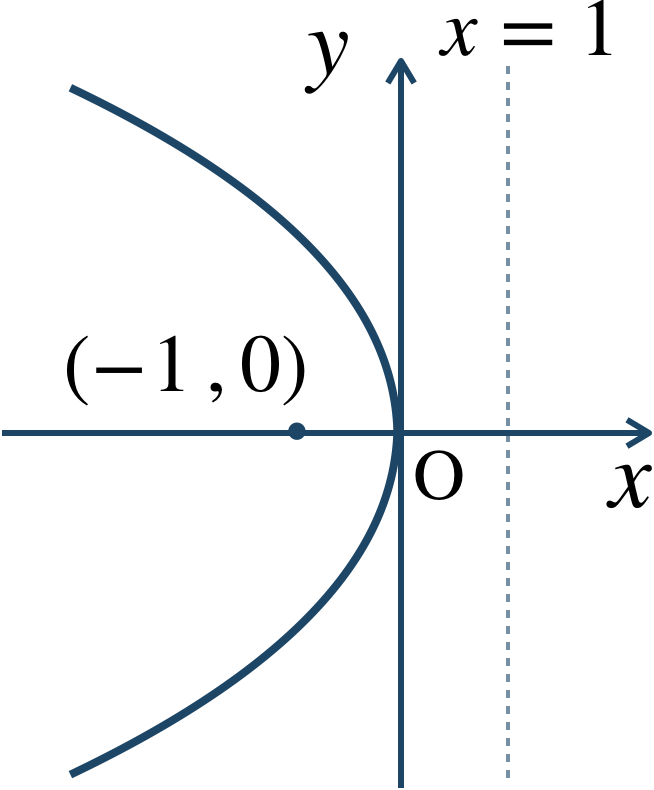
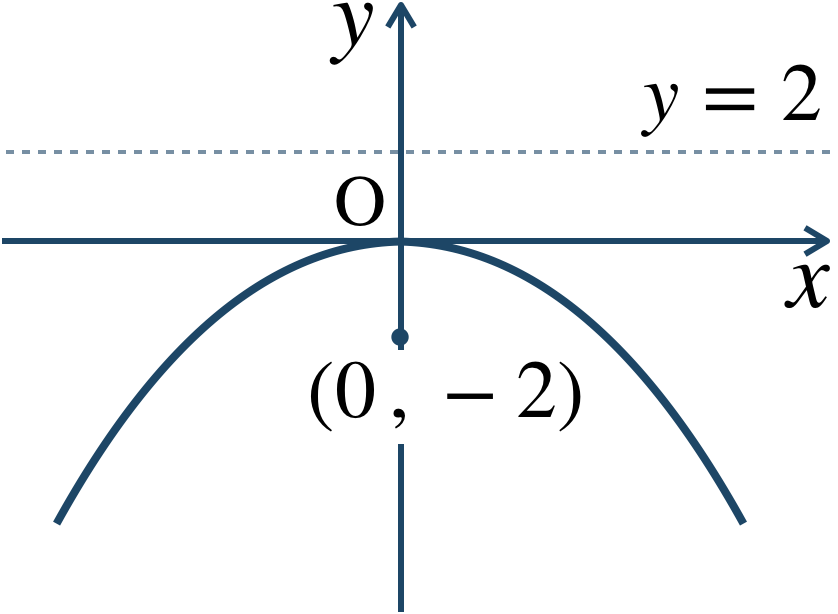
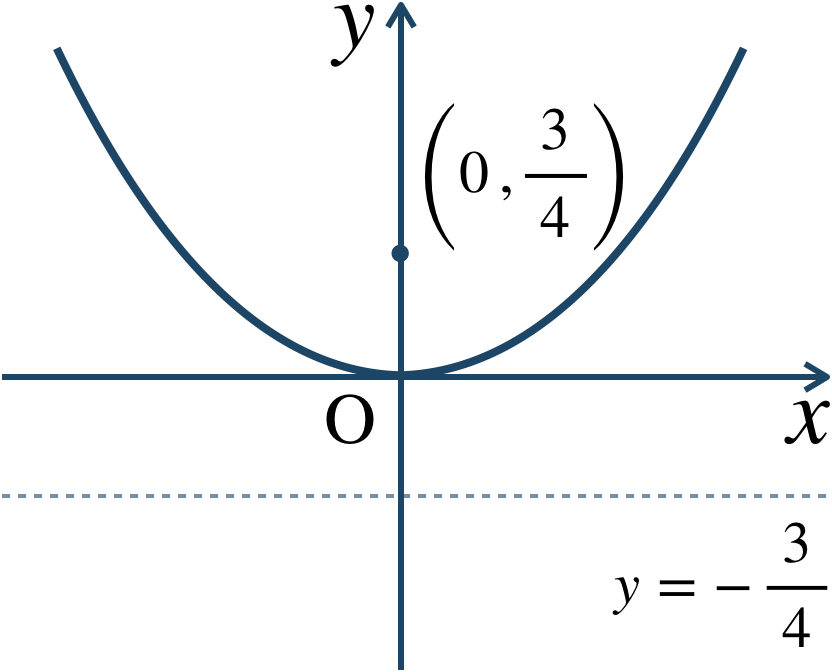
放物線の標準形

問題次の放物線の焦点と準線を求めて、概形をかけ。$${\small (1)}~y^2=12x~~~~~~~{\small (2)}~y^2=-4x$$$${\small (3)}~x^2=-8y~~~~~~{\small (4)}~x^2=3y$$

[ 解答を見る ]

【解答】
${\small (1)}~$焦点 $(3~,~0)$ 、準線 $x=-3$

${\small (2)}~$焦点 $(-1~,~0)$ 、準線 $x=1$

${\small (3)}~$焦点 $(0~,~-2)$ 、準線 $y=2$

${\small (4)}~$焦点 $(0~,~{\large \frac{\,3\,}{\,4\,}})$ 、準線 $y=-{\large \frac{\,3\,}{\,4\,}}$

詳しい解説ページはこちらから↓

放物線の標準形

今回は放物線の標準形ついて解説していきます。焦点や準線を求めて、概形をかけるようにしましょう。

放物線の方程式の決定

問題次の条件を満たす放物線の方程式を求めて、概形をかけ。
${\small (1)}~$焦点 $(-5~,~0)$ 、準線 $x=5$ の放物線。
${\small (2)}~$焦点 $(0~,~4)$ 、頂点 $(0~,~0)$ の放物線。

[ 解答を見る ]

【解答】 $${\small (1)}~y^2=-20x$$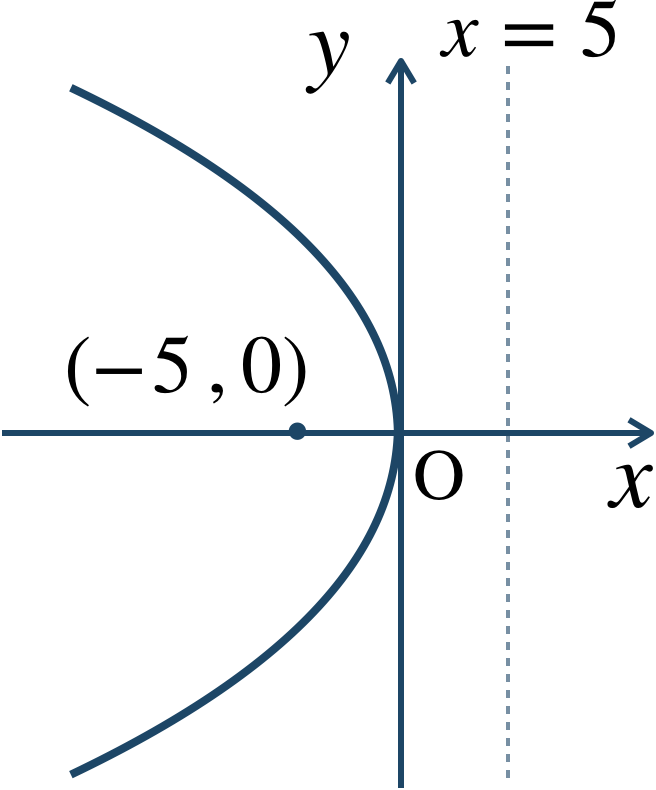
$${\small (2)}~x^2=16y$$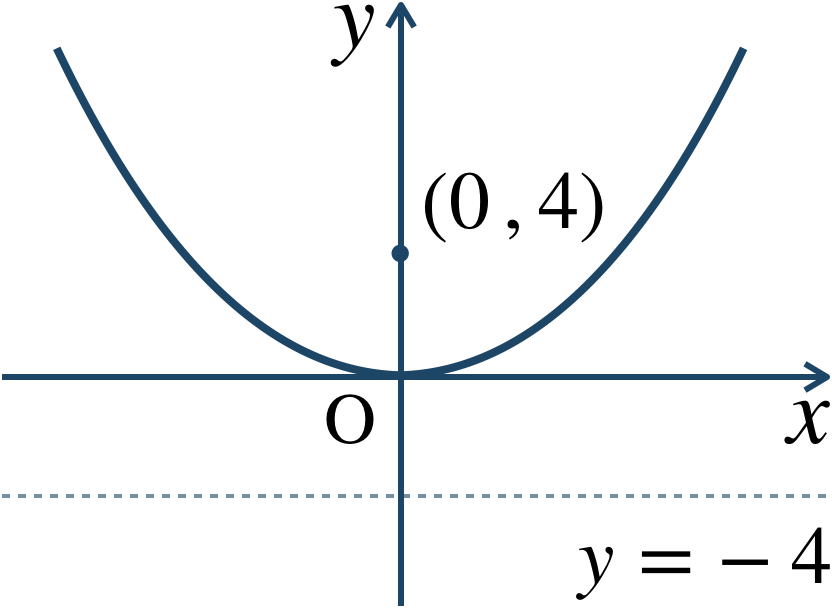

詳しい解説ページはこちらから↓

放物線の方程式の決定

今回は放物線の方程式の決定ついて解説していきます。まずは焦点や準線の条件より、どちらの放物線の標準形となるかを読み取りましょう。

楕円の標準形

問題次の問いに答えよ。
${\small (1)}~$次の楕円の長軸と短軸の長さ、焦点の座標を求めて、概形をかけ。$$~{\large ①}~\frac{\,x^2 \,}{\,25 \,}+\frac{\,y^2 \,}{\,9 \,}=1$$$$~{\large ②}~9x^2+4y^2=36$$${\small (2)}~$２点 $\left(\sqrt{7}~,~0\right)~,~\left(-\sqrt{7}~,~0\right)$ を焦点として、この２点からの距離の和が $8$ である楕円の方程式を求めよ。

[ 解答を見る ]

【解答】${\small (1)}~$
${\large ①}$長軸の長さ $10$、短軸の長さ $6$
焦点は、$$~~~{\rm F}(4~,~0)~,~{\rm F}'(-4~,~0)$$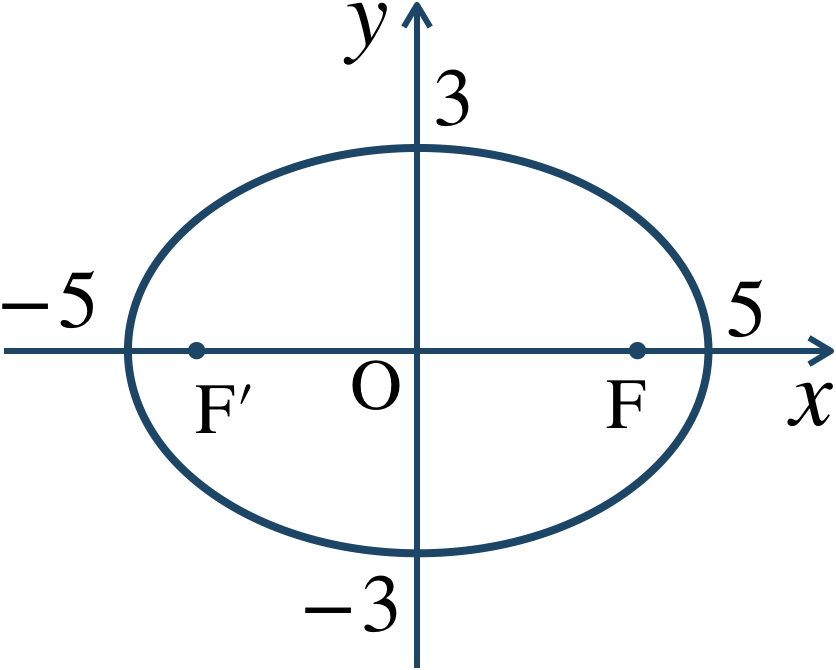
${\large ②}$長軸の長さ $6$、短軸の長さ $4$
焦点は、$$~~~{\rm F}\left(0~,~\sqrt{5}\right)~,~{\rm F}’\left(0~,~-\sqrt{5}\right)$$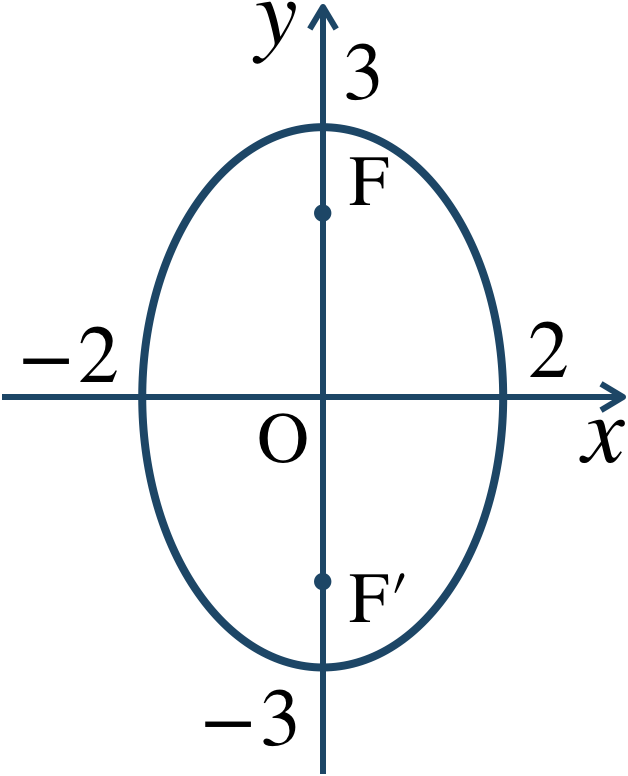
$${\small (2)}~\frac{\,x^2 \,}{\,16 \,}+\frac{\,y^2 \,}{\,9 \,}=1$$

詳しい解説ページはこちらから↓

楕円の標準形

今回は楕円の標準形ついて解説していきます。長軸と短軸の長さや焦点の求め方などをおさえておきましょう。

円と楕円の関係

問題次の問いに答えよ。
${\small (1)}~$円 $x^2+y^2=16$ を $x$ 軸をもとに $y$ 軸方向に ${\large \frac{\,3\,}{\,4\,}}$ 倍縮小した曲線を求めよ。
${\small (2)}~$円 $x^2+y^2=1$ を $x$ 軸をもとに $y$ 軸方向に $2$ 倍拡大した曲線を求めよ。

[ 解答を見る ]

【解答】$${\small (1)}~\frac{\,x^2 \,}{\,16 \,}+\frac{\,y^2 \,}{\, 9\,}=1$$$${\small (2)}~x^2+\frac{\,y^2 \,}{\, 4\,}=1$$

詳しい解説ページはこちらから↓

円と楕円の関係

今回は円と楕円の関係について解説していきます。円の方程式から楕円の方程式を求める手順を覚えていきましょう。

楕円と軌跡

問題長さ $3$ の線分 ${\rm AB}$ の両端 ${\rm A~,~B}$ がそれぞれ $x$ 軸上と $y$ 軸上を動くとき、線分 ${\rm AB}$ を $1\,:\,2$ に内分する点 ${\rm P}$ の軌跡を求めよ。

[ 解答を見る ]

【解答】
点 ${\rm P}$ の軌跡は、楕円 ${\large \frac{\,x^2 \,}{\,4 \,}}+y^2=1$

詳しい解説ページはこちらから↓

楕円の軌跡

今回は楕円の軌跡について解説していきます。線分の長さの条件と内分点の条件より、軌跡を求める手順を覚えていきましょう。

双曲線の標準形

問題次の双曲線の焦点と漸近線を求めて、概形をかけ。$${\small (1)}~\frac{\,x^2 \,}{\,16 \,}-\frac{\,y^2 \,}{\,9 \,}=1$$$${\small (2)}~25x^2-4y^2=100$$$${\small (3)}~\frac{\,x^2 \,}{\,25 \,}-\frac{\,y^2 \,}{\,16 \,}=-1$$$${\small (4)}~9x^2-4y^2=-36$$

[ 解答を見る ]

【解答】${\small (1)}~$焦点は、$$~~~{\rm F}(5~,~0)~,~{\rm F}'(-5~,~0)$$漸近線は、$$~~~y=\pm\frac{\,3 \,}{\,4 \,}x$$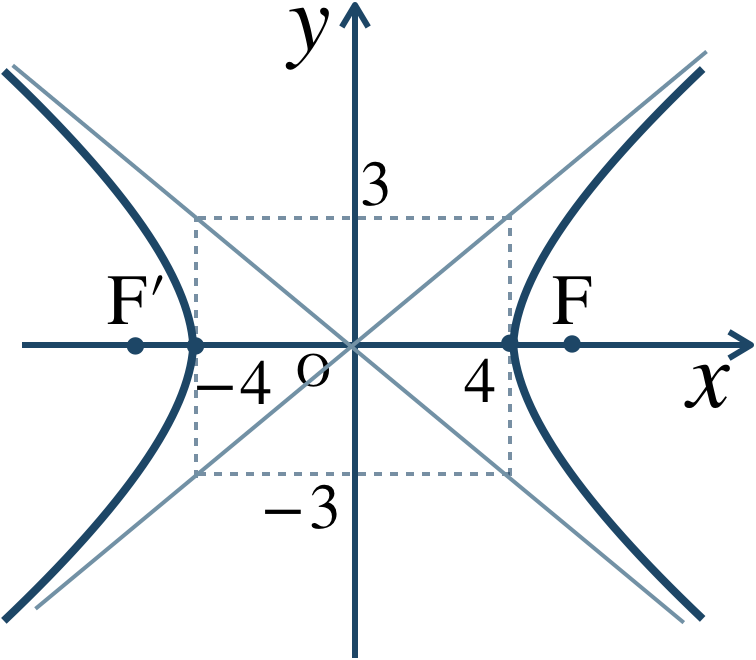
${\small (2)}~$焦点は、$$~~~{\rm F}\left(\sqrt{29}~,~0\right)~,~{\rm F}’\left(-\sqrt{29}~,~0\right)$$漸近線は、$$~~~y=\pm\frac{\,5 \,}{\,2 \,}x$$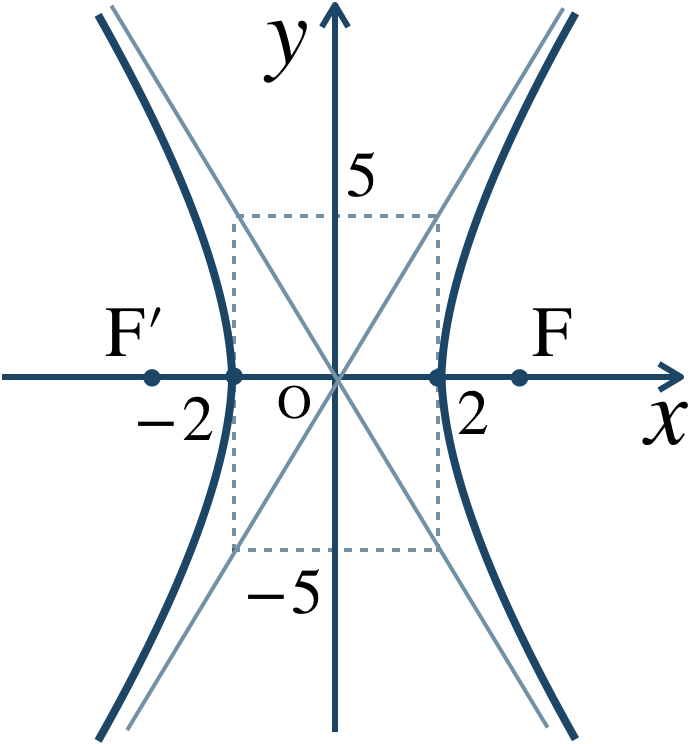
${\small (3)}~$焦点は、$$~~~{\rm F}\left(0~,~\sqrt{41}\right)~,~{\rm F}’\left(0~,~-\sqrt{41}\right)$$漸近線は、$$~~~y=\pm\frac{\,4 \,}{\,5 \,}x$$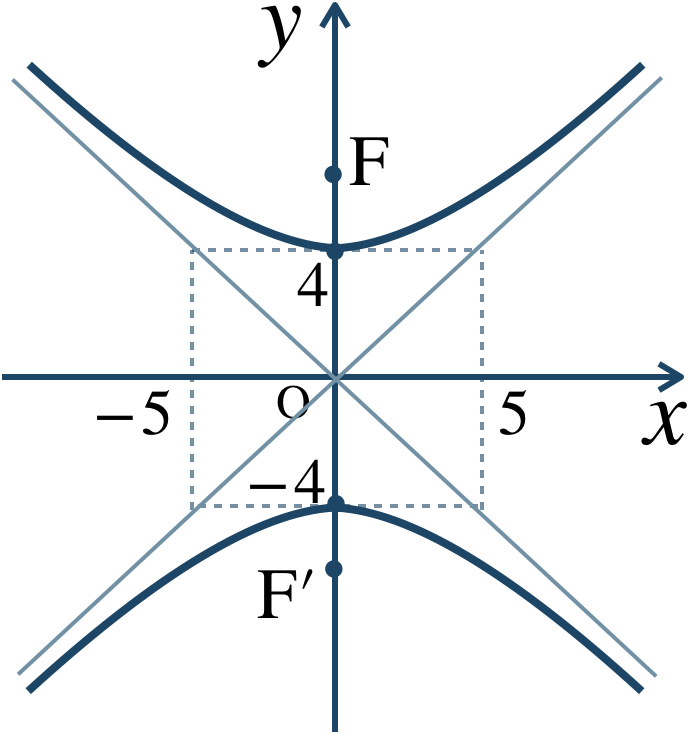
${\small (4)}~$焦点は、$$~~~{\rm F}\left(0~,~\sqrt{13}\right)~,~{\rm F}’\left(0~,~-\sqrt{13}\right)$$漸近線は、$$~~~y=\pm\frac{\,3 \,}{\,2 \,}x$$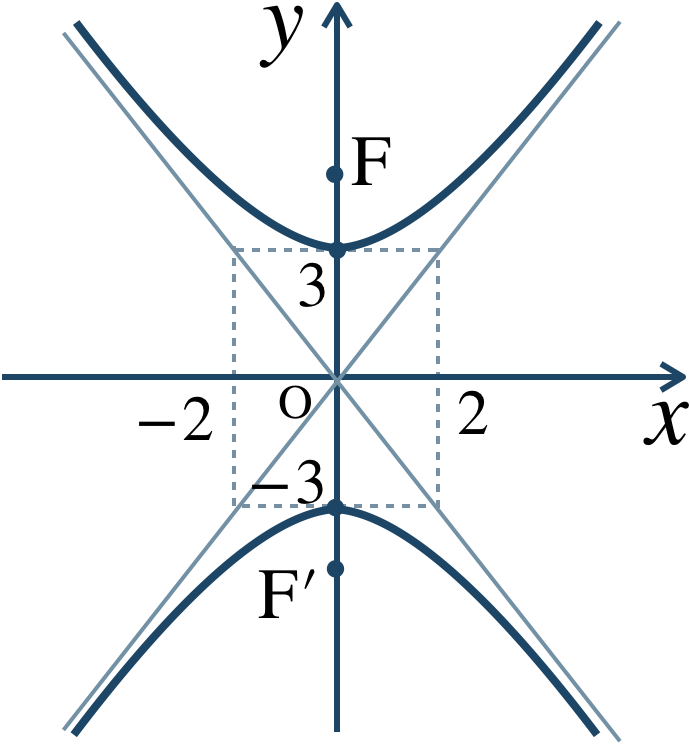

詳しい解説ページはこちらから↓

双曲線の標準形

今回は双曲線の標準形ついて解説していきます。焦点や漸近線の求め方をおさえておきましょう。

双曲線の方程式の決定

問題次の条件を満たす双曲線の方程式を求めよ。
${\small (1)}~$２点 $(5~,~0)~,~(-5~,~0)$ を焦点として、この２点からの距離の差が $6$ である。
${\small (2)}~$２点 $\left(0~,~\sqrt{5}\right)~,~\left(0~,~-\sqrt{5}\right)$ を焦点として、漸近線が直線 $y=\pm{\large \frac{\,1\,}{\,2\,}}x$ である。
${\small (3)}~$２点 $(2~,~0)~,~(-2~,~0)$ を焦点として、漸近線が直交する。

[ 解答を見る ]

【解答】$${\small (1)}~\frac{\,x^2 \,}{\,9 \,}-\frac{\,y^2 \,}{\,16 \,}=1$$$${\small (2)}~\frac{\,x^2 \,}{\,4 \,}-y^2=-1$$$${\small (3)}~\frac{\,x^2 \,}{\,2 \,}-\frac{\,y^2 \,}{\,2 \,}=1$$

詳しい解説ページはこちらから↓

双曲線の方程式の決定

今回は双曲線の方程式の決定ついて解説していきます。焦点の座標の条件やこの２点からの距離の差、漸近線の条件を式にできるようにしましょう。

２次曲線の平行移動

問題次の曲線を $x$ 軸方向に $2$ 、$y$ 軸方向に $-3$ だけ平行移動した曲線の方程式を求めよ。また、その焦点を求めよ。$${\small (1)}~y^2=20x$$$${\small (2)}~\frac{\,x^2 \,}{\,10 \,}+\frac{\,y^2 \,}{\,6 \,}=1$$$${\small (3)}~\frac{\,x^2 \,}{\,5 \,}-\frac{\,y^2 \,}{\,4 \,}=1$$

[ 解答を見る ]

【解答】
${\small (1)}~$放物線の方程式は、$$~~~(y+3)^2=20(x-2)$$焦点は $(7~,~-3)$
${\small (2)}~$楕円の方程式は、$$~~~\frac{\,(x-2)^2 \,}{\,10 \,}+\frac{\,(y+3)^2 \,}{\,6 \,}=1$$焦点は $(4~,~-3)$$~,~$$(0~,~-3)$
${\small (3)}~$楕円の方程式は、$$~~~\frac{\,(x-2)^2 \,}{\,5 \,}-\frac{\,(y+3)^2 \,}{\,4 \,}=1$$焦点は $(5~,~-3)$$~,~$$(-1~,~-3)$

詳しい解説ページはこちらから↓

２次曲線の平行移動

今回は２次曲線の平行移動ついて解説していきます。平行移動した曲線の方程式の求め方を覚えていきましょう。

平行移動後の２次曲線

問題次の方程式はどのような図形を表すか答えよ。また、焦点を求めよ。$${\small (1)}~y^2+4x-2y+13=0$$$${\small (2)}~5x^2+3y^2+10x+12y+2=0$$$${\small (3)}~3x^2-y^2-12x-2y+14=0$$

[ 解答を見る ]

【解答】
${\small (1)}~$$y^2=-4x$ を $x$ 軸方向に $-3$ 、$y$ 軸方向に $1$ 平行移動した放物線
焦点は、$(-4~,~1)$
${\small (2)}~$${\large \frac{\,x^2\,}{\,3\,}}+{\large \frac{\,y^2\,}{\,5\,}}=1$ を $x$ 軸方向に $-1$ 、$y$ 軸方向に $-2$ 平行移動した楕円
焦点は $\left(-1~,~\sqrt{2}-2\right)$$~,~$$\left(-1~,~-\sqrt{2}-2\right)$
${\small (3)}~$$x^2-{\large \frac{\,y^2\,}{\,3\,}}=-1$ を $x$ 軸方向に $2$ 、$y$ 軸方向に $-1$ 平行移動した双曲線
焦点は $(2~,~1)$$~,~$$(2~,~-3)$

詳しい解説ページはこちらから↓

平行移動後の２次曲線

今回は平行移動後の２次曲線ついて解説していきます。平方完成をすることで、どのような２次曲線を平行移動させた曲線かを読み取れるようになりましょう。

２次曲線と直線

問題次の２次曲線と直線は共有点をもつか答えよ。また、もつ場合はその共有点の座標を求めよ。$${\small (1)}~y^2=9x~,~y=x+2$$$${\small (2)}~x^2+3y^2=12~,~x-y=-4$$$${\small (3)}~3x^2-y^2=6~,~y=2x-1$$

[ 解答を見る ]

【解答】
${\small (1)}~$共有点を２つもち、$$~~~(1~,~3)~,~(4~,~6)$$${\small (2)}~$共有点を１つもち、$$~~~(-3~,~1)$$${\small (3)}~$共有点をもたない

詳しい解説ページはこちらから↓

２次曲線と直線

今回は２次曲線と直線との共有点ついて解説していきます。共有点の個数は判別式、共有点の座標は２次方程式の解を利用しましょう。

２次曲線と直線の共有点の個数

問題次の２次曲線と直線の共有点の個数を答えよ。$${\small (1)}~9x^2-y^2=9~,~y=kx$$$${\small (2)}~2x^2+3y^2=6~,~y=x+k$$

[ 解答を見る ]

【解答】
${\small (1)}~$
$-3\lt k \lt 3$ のとき、共有点２個
$k≦ -3~,~3≦ k$ のとき、共有点なし
${\small (2)}~$
$-\sqrt{5}\lt k \lt\sqrt{5}$ のとき、共有点２個
$k=\pm\sqrt{5}$ のとき、共有点１個
$k\lt-\sqrt{5}~,~ \sqrt{5}\lt k$ のとき、共有点なし

詳しい解説ページはこちらから↓

２次曲線と直線の共有点の個数

前回と同様に、２次曲線と直線の共有点の個数の調べ方について解説していきます。今回は定数が入っており、共有点をもつ条件を求める問題となります。

２次曲線の弦の長さと中点

問題楕円 $5x^2+y^2=5$ と直線 $y=2x+1$ が交わってできる弦について、次の問いに答えよ。
${\small (1)}~$弦の長さを求めよ。
${\small (2)}~$弦の中点の座標を求めよ。

[ 解答を見る ]

【解答】$${\small (1)}~\frac{\,20\sqrt{2} \,}{\,9 \,}$$$${\small (2)}~\left(-\frac{\,2 \,}{\,9 \,}~,~\frac{\,5 \,}{\,9 \,}\right)$$

詳しい解説ページはこちらから↓

２次曲線の弦の長さと中点

今回は２次曲線の弦の長さと中点について解説していきます。２次曲線と直線を連立した２次方程式について、解と係数の関係を用いる解法をおさえておきましょう。

２次曲線と接線

問題次の２次曲線の曲線上の点における接線の方程式を求めよ。$${\small (1)}~y^2=12x~,~(3~,~6)$$$${\small (2)}~3x^2+y^2=12~,~(-1~,~3)$$$${\small (3)}~4x^2-y^2=4~,~\left(\sqrt{2}~,~-2\right)$$

[ 解答を見る ]

【解答】$${\small (1)}~y=x+3$$$${\small (2)}~x-y=-4$$$${\small (3)}~2\sqrt{2}x+y=2$$

詳しい解説ページはこちらから↓

２次曲線と接線

今回は２次曲線と接線について解説していきます。接点がわかっているとき、放物線や楕円、双曲線の接線の方程式を覚えておきましょう。

外部の点から引いた２次曲線の接線

問題次の楕円に点 $(-1~,~8)$ から引いた接線の方程式を求めよ。$$~~~\frac{\,x^2 \,}{\,6 \,}+\frac{\,y^2 \,}{\,12 \,}=1$$

[ 解答を見る ]

【解答】$$~~~2x+y=6~,~26x-5y=-66$$

詳しい解説ページはこちらから↓

外部の点から引いた２次曲線の接線

今回は外部の点から引いた２次曲線の接線について解説していきます。接点の座標を文字で置くところから解法をスタートさせましょう。

２次曲線と離心率

問題点 $(3~,~0)$ と直線 $x=5$ からの距離の比が $e\,:\,1$ である点 ${\rm P}$ について、$e$ の値が次のときの点 ${\rm P}$ の軌跡を求めよ。$${\small (1)}~e=1~~~~~{\small (2)}~e=\sqrt{3}~~~~~{\small (3)}~e=\frac{\,1 \,}{\,\sqrt{3} \,}$$

[ 解答を見る ]

【解答】
${\small (1)}~$放物線 $y^2=-4x$ を $x$ 軸方向に$4$ 平行移動した放物線
${\small (2)}~$双曲線 ${\large \frac{\,x^2\,}{\,3\,}}-{\large \frac{\,y^2\,}{\,6\,}}=1$ を $x$ 軸方向に$6$ 平行移動した双曲線
${\small (3)}~$楕円 ${\large \frac{\,x^2\,}{\,3\,}}+{\large \frac{\,y^2\,}{\,2\,}}=1$ を $x$ 軸方向に$2$ 平行移動した楕円

詳しい解説ページはこちらから↓

２次曲線と離心率

今回は２次曲線と離心率について解説していきます。離心率と定義と、離心率の値から２次曲線の軌跡を求める手順を覚えておきましょう。

曲線の媒介変数表示

問題次の媒介変数表示はどのような曲線となるか答えよ。$${\small (1)}~\left\{ \begin{array}{l} x=2t^2 \\ y=4t \end{array}\right.$$$${\small (2)}~\left\{ \begin{array}{l} x=3\cos{\theta}+1 \\ y=3\sin{\theta} \end{array}\right.$$$${\small (3)}~\left\{ \begin{array}{l} x=4\cos{\theta}-3 \\ y=3\sin{\theta}+2 \end{array}\right.$$$${\small (4)}~\left\{ \begin{array}{l} x={\large \frac{\,3 \,}{\,\cos{\theta} \,}} \\ y=2\tan{\theta} \end{array}\right.$$

[ 解答を見る ]

【解答】
${\small (1)}~$放物線 $y^2=8x$
${\small (2)}~$円 $(x-1)^2+y^2=9$
${\small (3)}~$楕円 ${\large \frac{\,(x+3)^2\,}{\,16\,}}+{\large \frac{\,(y-2)^2\,}{\,9\,}}=1$
${\small (4)}~$双曲線 ${\large \frac{\,x^2\,}{\,9\,}}-{\large \frac{\,y^2\,}{\,4\,}}=1$

詳しい解説ページはこちらから↓

曲線の媒介変数表示

今回は曲線の媒介変数表示について解説していきます。媒介変数を消去しもとの曲線の方程式にする方法を覚えておきましょう。

放物線の頂点が描く曲線

問題放物線 $y=x^2-tx+t^2-3t+1$ の頂点は、$t$ の値によってどのような曲線上を動くか求めよ。

[ 解答を見る ]

【解答】
放物線 $y=3x^2-6x+1$

詳しい解説ページはこちらから↓

放物線の頂点が描く曲線

今回は放物線の頂点が描く曲線について解説していきます。平方完成して頂点を求めて、頂点の式から軌跡を求める手順をおさえておきましょう。

極座標と直交座標

問題次の問いに答えよ。
${\small (1)}~$次の極座標を図示し、直交座標で表せ。$$~{\large ①}~{\rm A}\left(2~,~\frac{\,\pi \,}{\,3 \,}\right)~~~~~~\,{\large ②}~{\rm B}\left(4~,~-\frac{\,\pi \,}{\,4 \,}\right)$$$$~{\large ③}~{\rm C}\left(3~,~\frac{\,3 \,}{\,2 \,}\pi\right)~~~~{\large ④}~{\rm D}(1~,~\pi)$$${\small (2)}~$次の直交座標を極座標で表せ。$$~{\large ①}~{\rm E}(-1~,~1)~~~~~~{\large ②}~{\rm F}\left(3~,~\sqrt{3}\right)$$$$~{\large ③}~{\rm G}(0~,~4)~~~~~~~~{\large ④}~{\rm H}(2~,~0)$$

[ 解答を見る ]

【解答】${\small (1)}~$
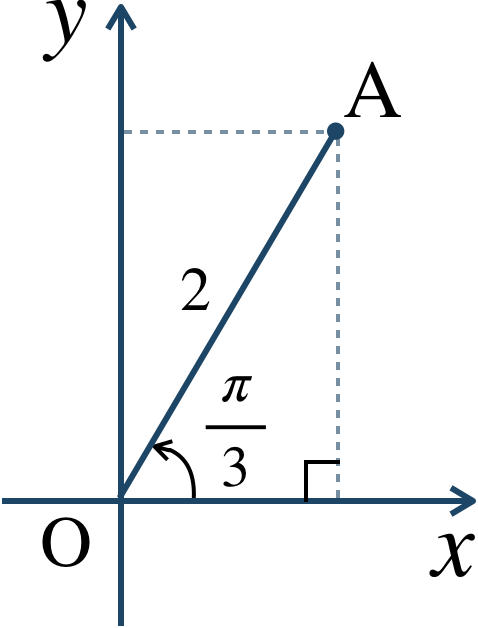
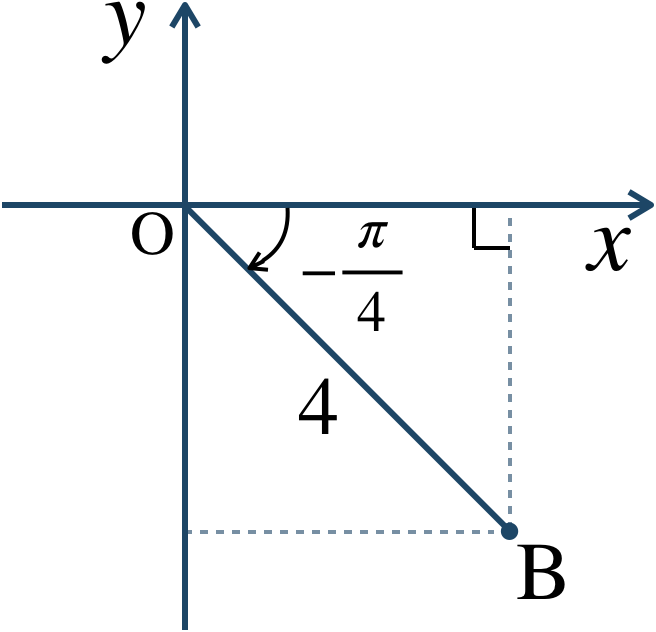
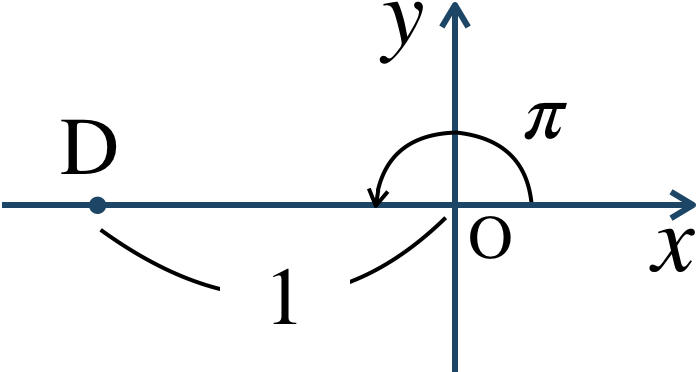
$${\large ①}~\left(1~,~\sqrt{3}\right)$$$${\large ②}~\left(2\sqrt{2}~,~-2\sqrt{2}\right)$$$${\large ③}~(0~,~-3)$$$${\large ④}~(-1~,~0)$$
${\small (2)}~$$${\large ①}~\left(\sqrt{2}~,~\frac{\,3 \,}{\,4 \,}\pi\right)$$$${\large ②}~\left(2\sqrt{3}~,~\frac{\,\pi \,}{\,6 \,}\right)$$$${\large ③}~\left(4~,~\frac{\,\pi \,}{\,2 \,}\right)$$$${\large ④}~\left(2~,~0\right)$$

詳しい解説ページはこちらから↓

極座標と直交座標

今回は極座標と直交座標について解説していきます。極座標を図示できることと、極座標と直交座標の相互変換ができるようになりましょう。

極方程式

問題次の極方程式はどのような図形を表すか答えよ。$${\small (1)}~r=3~~~~~~~~~~~~~\,{\small (2)}~\theta=\frac{\,\pi \,}{\,3 \,}$$$${\small (3)}~r=\frac{\,5 \,}{\,\sin{\theta} \,}~~~~~{\small (4)}~r=\frac{\,4\cos{\theta} \,}{\,\sin^2{\theta} \,}$$$${\small (5)}~\frac{\,1 \,}{\,r \,}=3\sin{\theta}+4\cos{\theta}$$$${\small (6)}~r=6\sin{\theta}+4\cos{\theta}$$

[ 解答を見る ]

【解答】
${\small (1)}~$極 ${\rm O}$ を中心とする半径 $3$ の円
${\small (2)}~$始線とのなす角が ${\large \frac{\,\pi\,}{\,3\,}}$ の直線の方程式
${\small (3)}~$直線 $y=5$
${\small (4)}~$放物線 $y^2=4x$
${\small (5)}~$直線 $4x+3y=1$
${\small (6)}~$中心 $(2~,~3)$ で半径 $\sqrt{13}$ の円

詳しい解説ページはこちらから↓

極方程式

今回は極方程式について解説していきます。極方程式を直行座標の方程式に変換する方法を覚えておきましょう。

極方程式と直交座標

問題次の直交座標で表された曲線の方程式を極方程式にせよ。$${\small (1)}~x^2+y^2=25$$$${\small (2)}~y^2=12x$$$${\small (3)}~3x^2+2y^2=6$$$${\small (4)}~(x+1)^2+y^2=1$$

[ 解答を見る ]

【解答】$${\small (1)}~r=5$$$${\small (2)}~r={ \frac{\,12\cos{\theta}\,}{\,\sin^2{\theta}\,}}$$$${\small (3)}~r^2(3-\sin^2{\theta})=6$$または、$$~~~r^2(\cos^2{\theta}+2)=6$$$${\small (4)}~r=-2\cos{\theta}$$

詳しい解説ページはこちらから↓

極方程式と直交座標

今回は直交座標で表された曲線の方程式を極方程式にする解法について解説していきます。x と y を変換する手順をおさえておきましょう。

２次曲線の極方程式

問題原点が１つの焦点、準線が $x=-a$ 、離心率が $e$ である２次曲線の極方程式は$$~~~r=\frac{\,ea \,}{\,1-e\cos{\theta} \,}$$で表される。
$e~,~a$ が次の値をとるとき、どのような曲線となるか答えよ。 $${\small (1)}~e=1~,~a=3$$$${\small (2)}~e=\sqrt{3}~,~a=2$$$${\small (3)}~e=\frac{\,1 \,}{\,\sqrt{3} \,}~,~a=4$$

[ 解答を見る ]

【解答】
${\small (1)}~$放物線 $y^2=6x+9$
${\small (2)}~$双曲線 ${\large \frac{\,(x+3)^2\,}{\,3\,}}-{\large \frac{\,y^2\,}{\,6\,}}=1$
${\small (3)}~$楕円 ${\large \frac{\,(x-2)^2\,}{\,12\,}}+{\large \frac{\,y^2\,}{\,8\,}}=1$

詳しい解説ページはこちらから↓