双曲線の標準形

2020.09.29

双曲線の標準形の解法
問題解説：双曲線の標準形
今回のまとめ

双曲線の標準形の解法

Point：双曲線の標準形２つの焦点からの距離の差が一定である点の軌跡を双曲線という。
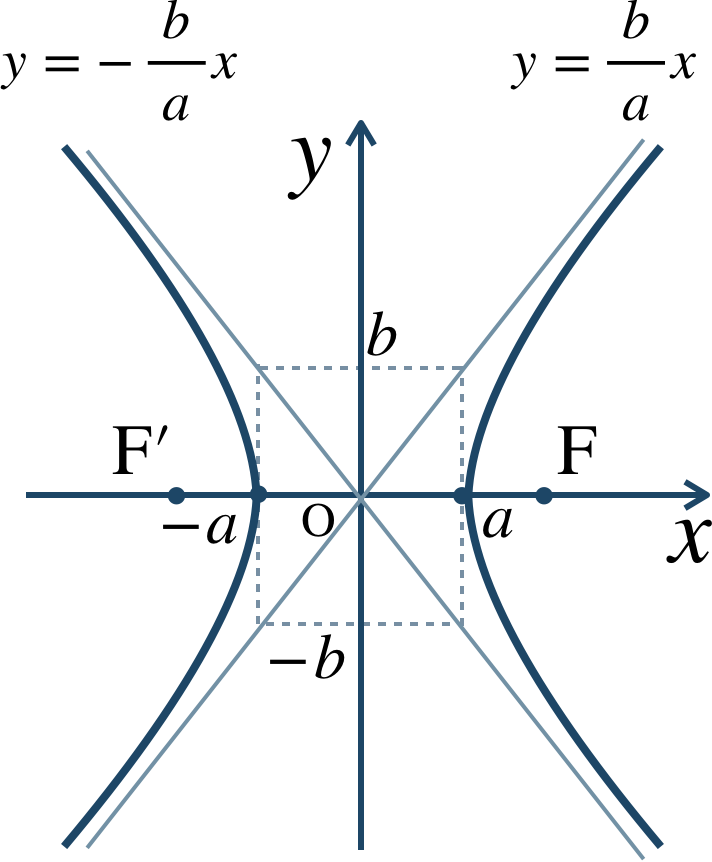
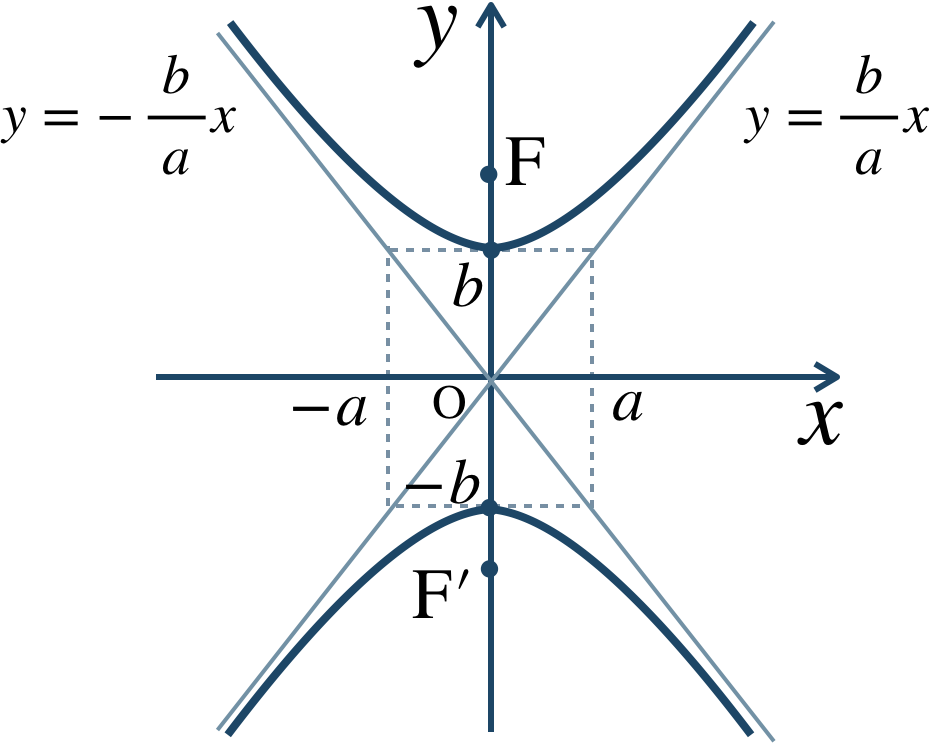
(1) 焦点が $x$ 軸上にある双曲線

$$\frac{\,x^2 \,}{\,a^2 \,}-\frac{\,y^2 \,}{\,b^2 \,}=1$$

ただし、$a\gt0~,~b\gt0$
$c=\sqrt{a^2+b^2}$ としたとき、焦点は、$$~~~{\rm F}(c~,~0)~,~{\rm F}'(-c~,~0)$$また、原点 $(0~,~0)$ が中心で、点 $(a~,~0)$$~,~$$(-a~,~0)$ が頂点となり、焦点からの距離の差が $2a$ となる。
漸近線は、$$~~~\frac{\,x \,}{\,a \,}-\frac{\,y \,}{\,b \,}=0~,~\frac{\,x \,}{\,a \,}+\frac{\,y \,}{\,b \,}=0$$すなわち、$$~~~~~y=\pm\frac{\,b \,}{\,a \,}x$$概形は、

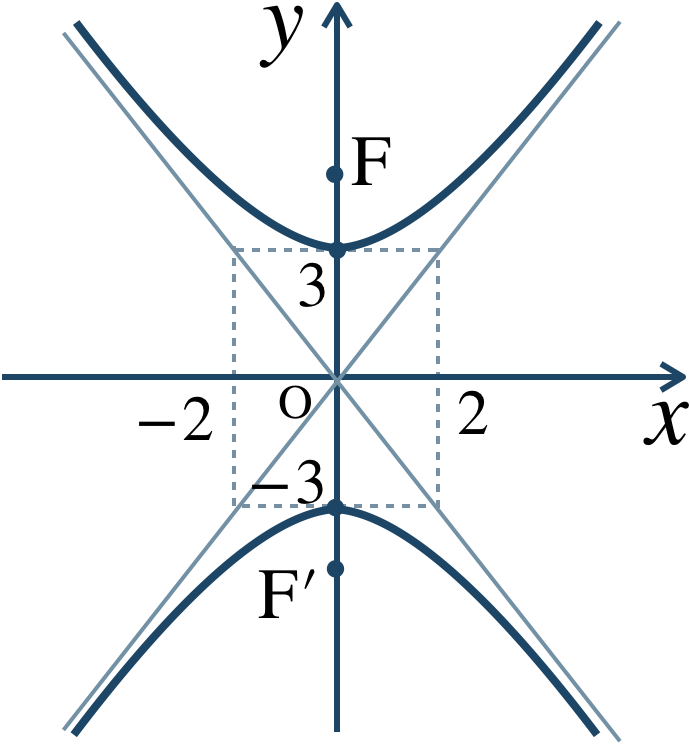
(2) 焦点が $y$ 軸上にある双曲線

$$~~~\frac{\,x^2 \,}{\,a^2 \,}-\frac{\,y^2 \,}{\,b^2 \,}=-1$$

ただし、$a\gt0~,~b\gt0$
$c=\sqrt{a^2+b^2}$ としたとき、焦点は、$$~~~{\rm F}(0~,~c)~,~{\rm F}'(0~,~-c)$$また、原点 $(0~,~0)$ が中心で、点 $(0~,~b)$$~,~$$(0~,~-b)$ が頂点となり、焦点からの距離の差が $2b$ となる。
漸近線は、$$~~~\frac{\,x \,}{\,a \,}-\frac{\,y \,}{\,b \,}=0~,~\frac{\,x \,}{\,a \,}+\frac{\,y \,}{\,b \,}=0$$すなわち、$$~~~~~y=\pm\frac{\,b \,}{\,a \,}x$$概形は、

問題解説：双曲線の標準形

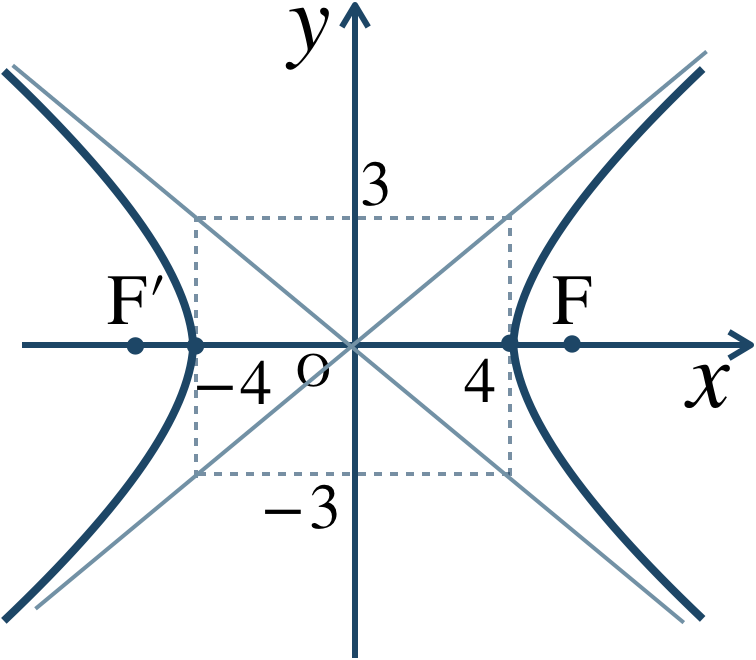
問題解説(1)

問題次の双曲線の焦点と漸近線を求めて、概形をかけ。$${\small (1)}~\frac{\,x^2 \,}{\,16 \,}-\frac{\,y^2 \,}{\,9 \,}=1$$

与式より、$$~~~\frac{\,x^2 \,}{\,4^2 \,}-\frac{\,y^2 \,}{\,3^2 \,}=1$$焦点が $x$ 軸上にある双曲線であり、$a=4~,~b=3$ となる。
また、$c=\sqrt{a^2+b^2}$ より、$$~~~c=\sqrt{4^2+3^2}$$$$~~~~\,=\sqrt{16+9}$$$$~~~~\,=\sqrt{25}=5$$よって、焦点は、$$~~~{\rm F}(5~,~0)~,~{\rm F}'(-5~,~0)$$また、漸近線は、$$~~~\frac{\,x \,}{\,4 \,}-\frac{\,y \,}{\,3 \,}=0~,~\frac{\,x \,}{\,4 \,}+\frac{\,y \,}{\,3\,}=0$$それぞれを式変形すると、$$~~~-\frac{\, y\,}{\,3 \,}=-\frac{\,x \,}{\,4 \,}~~\Leftrightarrow~~y=\frac{\,3 \,}{\,4 \,}x$$$$~~~~~~~\frac{\, y\,}{\,3 \,}=-\frac{\,x \,}{\,4 \,}~~\Leftrightarrow~~y=-\frac{\,3 \,}{\,4 \,}x$$したがって、$$~~~y=\pm\frac{\,3 \,}{\,4 \,}x$$概形は、

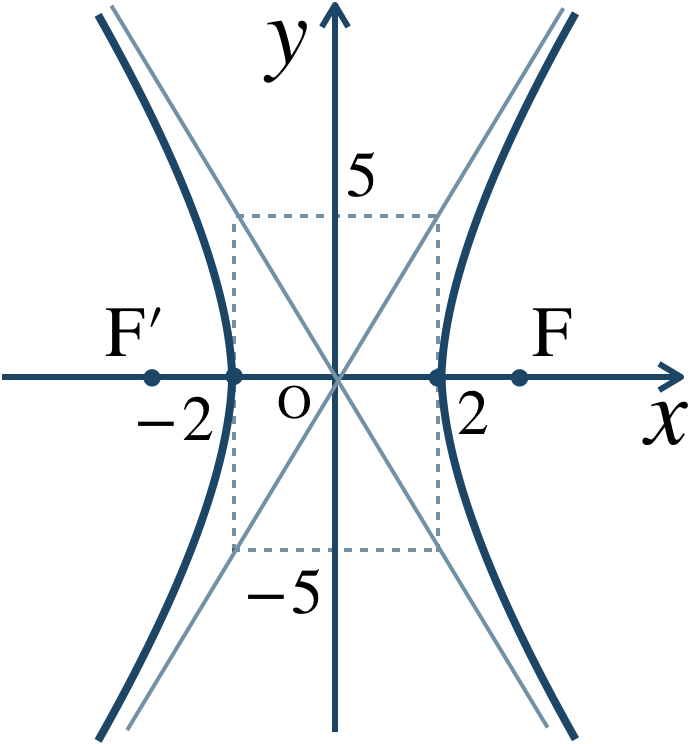
問題解説(2)

問題次の双曲線の焦点と漸近線を求めて、概形をかけ。$${\small (2)}~25x^2-4y^2=100$$

両辺を $\div100$ すると、$$~~~\frac{\,25x^2 \,}{\,100 \,}-\frac{\,4y^2 \,}{\,100 \,}=\frac{\,100 \,}{\,100 \,}$$よって、計算すると、$$~~~\frac{\,x^2 \,}{\,2^2 \,}-\frac{\,y^2 \,}{\,5^2 \,}=1$$焦点が $x$ 軸上にある双曲線であり、$a=2~,~b=5$ となる。
また、$c=\sqrt{a^2+b^2}$ より、$$~~~c=\sqrt{2^2+5^2}$$$$~~~~\,=\sqrt{4+25}$$$$~~~~\,=\sqrt{29}$$よって、焦点は、$$~~~{\rm F}\left(\sqrt{29}~,~0\right)~,~{\rm F}’\left(-\sqrt{29}~,~0\right)$$また、漸近線は、$$~~~\frac{\,x \,}{\,2 \,}-\frac{\,y \,}{\,5 \,}=0~,~\frac{\,x \,}{\,2 \,}+\frac{\,y \,}{\,5\,}=0$$それぞれを式変形すると、$$~~~-\frac{\, y\,}{\,5 \,}=-\frac{\,x \,}{\,2 \,}~~\Leftrightarrow~~y=\frac{\,5 \,}{\,2 \,}x$$$$~~~~~~~\frac{\, y\,}{\,5 \,}=-\frac{\,x \,}{\,2 \,}~~\Leftrightarrow~~y=-\frac{\,5 \,}{\,2 \,}x$$したがって、$$~~~y=\pm\frac{\,5 \,}{\,2 \,}x$$概形は、

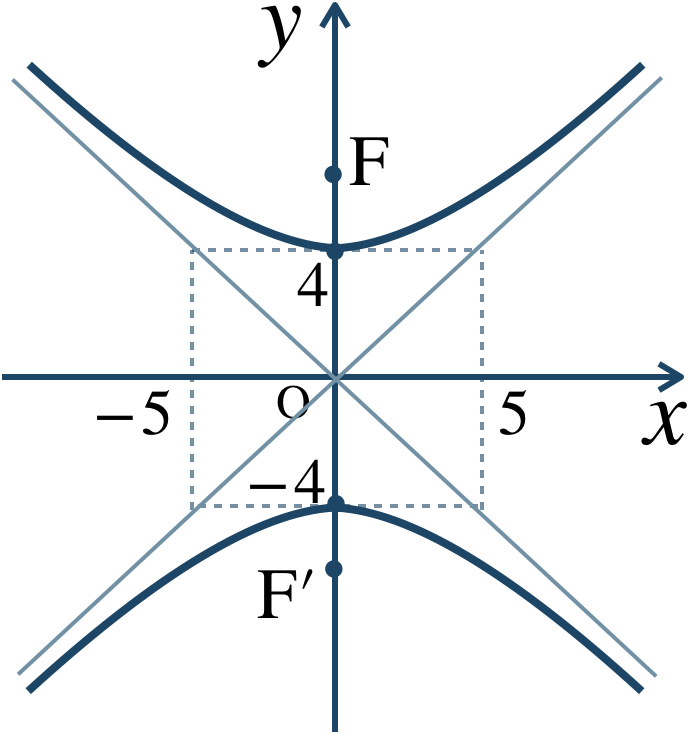
問題解説(3)

問題次の双曲線の焦点と漸近線を求めて、概形をかけ。$${\small (3)}~\frac{\,x^2 \,}{\,25 \,}-\frac{\,y^2 \,}{\,16 \,}=-1$$

与式より、$$~~~\frac{\,x^2 \,}{\,5^2 \,}-\frac{\,y^2 \,}{\,4^2 \,}=-1$$焦点が $y$ 軸上にある双曲線であり、$a=5~,~b=4$ となる。
また、$c=\sqrt{a^2+b^2}$ より、$$~~~c=\sqrt{5^2+4^2}$$$$~~~~\,=\sqrt{25+16}$$$$~~~~\,=\sqrt{41}$$よって、焦点は、$$~~~{\rm F}\left(0~,~\sqrt{41}\right)~,~{\rm F}’\left(0~,~-\sqrt{41}\right)$$また、漸近線は、$$~~~\frac{\,x \,}{\,5 \,}-\frac{\,y \,}{\,4 \,}=0~,~\frac{\,x \,}{\,5 \,}+\frac{\,y \,}{\,4\,}=0$$それぞれを式変形すると、$$~~~-\frac{\, y\,}{\,4 \,}=-\frac{\,x \,}{\,5 \,}~~\Leftrightarrow~~y=\frac{\,4 \,}{\,5 \,}x$$$$~~~~~~~\frac{\, y\,}{\,4 \,}=-\frac{\,x \,}{\,5 \,}~~\Leftrightarrow~~y=-\frac{\,4 \,}{\,5 \,}x$$したがって、$$~~~y=\pm\frac{\,4 \,}{\,5 \,}x$$概形は、

問題解説(4)

問題次の双曲線の焦点と漸近線を求めて、概形をかけ。$${\small (4)}~9x^2-4y^2=-36$$

両辺を $\div36$ すると、$$~~~\frac{\,9x^2 \,}{\,36 \,}-\frac{\,4y^2 \,}{\,36 \,}=-\frac{\,36 \,}{\,36 \,}$$よって、計算すると、$$~~~\frac{\,x^2 \,}{\,2^2 \,}-\frac{\,y^2 \,}{\,3^2 \,}=-1$$焦点が $y$ 軸上にある双曲線であり、$a=2~,~b=3$ となる。
また、$c=\sqrt{a^2+b^2}$ より、$$~~~c=\sqrt{2^2+3^2}$$$$~~~~\,=\sqrt{4+9}$$$$~~~~\,=\sqrt{13}$$よって、焦点は、$$~~~{\rm F}\left(0~,~\sqrt{13}\right)~,~{\rm F}’\left(0~,~-\sqrt{13}\right)$$また、漸近線は、$$~~~\frac{\,x \,}{\,2 \,}-\frac{\,y \,}{\,3 \,}=0~,~\frac{\,x \,}{\,2 \,}+\frac{\,y \,}{\,3\,}=0$$それぞれを式変形すると、$$~~~-\frac{\, y\,}{\,3 \,}=-\frac{\,x \,}{\,2 \,}~~\Leftrightarrow~~y=\frac{\,3 \,}{\,2 \,}x$$$$~~~~~~~\frac{\, y\,}{\,3 \,}=-\frac{\,x \,}{\,2 \,}~~\Leftrightarrow~~y=-\frac{\,3 \,}{\,2 \,}x$$したがって、$$~~~y=\pm\frac{\,3 \,}{\,2 \,}x$$概形は、