文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
演習問題
1章 場合の数と確率
p.148
1
\(185\)
1
\(185\)
p.148
2
\({\small (1)}~30\) \({\small (2)}~15\) \({\small (3)}~6\)
2
\({\small (1)}~30\) \({\small (2)}~15\) \({\small (3)}~6\)
p.148
3
\({\small (1)}~{\Large \frac{3}{8}}\) \({\small (2)}~{\Large \frac{3}{16}}\)
3
\({\small (1)}~{\Large \frac{3}{8}}\) \({\small (2)}~{\Large \frac{3}{16}}\)
p.148
4
\({\small (1)}~{\Large \frac{4}{27}}\) \({\small (2)}~{\Large \frac{2}{9}}\) \({\small (3)}~{\Large \frac{196}{729}}\)
4
\({\small (1)}~{\Large \frac{4}{27}}\) \({\small (2)}~{\Large \frac{2}{9}}\) \({\small (3)}~{\Large \frac{196}{729}}\)
p.148
5
\({\Large \frac{20}{61}}\)
5
\({\Large \frac{20}{61}}\)
2章 整数の性質
p.149
1
\({\small (1)}~9~,~217\) \({\small (2)}~{\Large \frac{217}{100}}\)
\({\small (3)}~2^9\times5^9\)
1
\({\small (1)}~9~,~217\) \({\small (2)}~{\Large \frac{217}{100}}\)
\({\small (3)}~2^9\times5^9\)
p.149
2
[証明] \(2^n-1~,~2^n~,~2^n+1\) は連続する3つの整数であり、少なくとも1つは3の倍数である
また、\(2^n\) は2の倍数であり、3の倍数ではない
したがって、\(2^n-1\) と \(2^n+1\) の少なくとも一方は3の倍数である [終]
2
[証明] \(2^n-1~,~2^n~,~2^n+1\) は連続する3つの整数であり、少なくとも1つは3の倍数である
また、\(2^n\) は2の倍数であり、3の倍数ではない
したがって、\(2^n-1\) と \(2^n+1\) の少なくとも一方は3の倍数である [終]
p.149
3
[証明] \(n\) と\(n+1\) の最大公約数を \(g\) とすると、整数 \(s~,~t\) を用いて、
\(n=gs~,~n+1=gt\)
よって、これらより \(n\) を消去すると、
\(g\cdot(t-s)=1\)
ここで、\(t-s\) は整数であるので、\(g\) は正の約数となり \(g=1\)
したがって、\(n\) と \(n+1\) は互いに素である [終]
3
[証明] \(n\) と\(n+1\) の最大公約数を \(g\) とすると、整数 \(s~,~t\) を用いて、
\(n=gs~,~n+1=gt\)
よって、これらより \(n\) を消去すると、
\(g\cdot(t-s)=1\)
ここで、\(t-s\) は整数であるので、\(g\) は正の約数となり \(g=1\)
したがって、\(n\) と \(n+1\) は互いに素である [終]
p.149
4
\(a=2~,~b=5~,~c=10\)
4
\(a=2~,~b=5~,~c=10\)
p.149
5
\({\small (1)}~\)[証明] 整数 \(n\) を \(6\) で割った余りで分類すると、整数 \(k\) を用いて、
\(6k~,~6k+1~,~6k+2~,~6k+3\)
\(6k+4~,~6k+5\)
ここで、\(6k~,~6k+2~,~6k+4\) は2の倍数
\(6k+3\) は3の倍数となる
よって、\(3\) より大きい素数は
\(6k+1\) または \(6k+5\)
となる
したがって、\(3\) より大きい素数を \(6\) で割った余りは \(1\) または \(5\) である [終]
\({\small (2)}~\) [証明] \(p\) は \(3\) より大きい素数より、(1) より自然数 \(k\) を用いて、
\(p=6k+1~,~p=6k+5\)
(ⅰ) \(p=6k+1\) のとき、
\(p+2=6k+1+2=3(2k+1)\)
よって、\(p+2\) は素数ではない
(ⅱ) \(p=6k+5\) のとき、
\(p+2=6k+5+2=6k+7\)
このとき、\(p+2\) は素数である
よって、(ⅱ)のとき
\(p+1=6k+5+1=6(k+1)\)
したがって、\(p+1\) は \(6\) の倍数である [終]
5
\({\small (1)}~\)[証明] 整数 \(n\) を \(6\) で割った余りで分類すると、整数 \(k\) を用いて、
\(6k~,~6k+1~,~6k+2~,~6k+3\)
\(6k+4~,~6k+5\)
ここで、\(6k~,~6k+2~,~6k+4\) は2の倍数
\(6k+3\) は3の倍数となる
よって、\(3\) より大きい素数は
\(6k+1\) または \(6k+5\)
となる
したがって、\(3\) より大きい素数を \(6\) で割った余りは \(1\) または \(5\) である [終]
\({\small (2)}~\) [証明] \(p\) は \(3\) より大きい素数より、(1) より自然数 \(k\) を用いて、
\(p=6k+1~,~p=6k+5\)
(ⅰ) \(p=6k+1\) のとき、
\(p+2=6k+1+2=3(2k+1)\)
よって、\(p+2\) は素数ではない
(ⅱ) \(p=6k+5\) のとき、
\(p+2=6k+5+2=6k+7\)
このとき、\(p+2\) は素数である
よって、(ⅱ)のとき
\(p+1=6k+5+1=6(k+1)\)
したがって、\(p+1\) は \(6\) の倍数である [終]
p.149
6
\({\small (1)}~\)[証明] \(2≦p< q\) で \(pq\) が完全数とするとき、正の約数は
\(1~,~p~,~q~,~pq\)
よって、
\(1+p+q=pq\)
式変形すると、
\((p-1)(q-1)=1\)
ここで、\(1≦p-1<q-1\) より
\(p-1=1\) かつ \(q-1=2\)
よって、\(p=2~,~q=3\)
これより、\(pq=6\)
したがって、\(pq\) という形の完全数は \(6\) だけである [終]
\({\small (2)}~28\)
6
\({\small (1)}~\)[証明] \(2≦p< q\) で \(pq\) が完全数とするとき、正の約数は
\(1~,~p~,~q~,~pq\)
よって、
\(1+p+q=pq\)
式変形すると、
\((p-1)(q-1)=1\)
ここで、\(1≦p-1<q-1\) より
\(p-1=1\) かつ \(q-1=2\)
よって、\(p=2~,~q=3\)
これより、\(pq=6\)
したがって、\(pq\) という形の完全数は \(6\) だけである [終]
\({\small (2)}~28\)
p.149
7
\({\small (1)}~1~,~2~,~-4\)
\({\small (2)}~\)[証明] 任意の実数 \(x\) を \(p\) を整数、\(q\) を \(0≦q<1\) として \(x=p+q\) とすると、
(ⅰ) \(0≦q<{\large \frac{1}{2}}\) のとき
\(p≦p+q<p+{\large \frac{1}{2}}\) となり
\([x]=p\)
\(p+{\large \frac{1}{2}}≦p+q+{\large \frac{1}{2}}<p+1\) となり
\(\left[x+{\large \frac{1}{2}}\right]=p\)
\(2p≦2p+2q<2p+1\) となり
\([2x]=2p\)
よって、
(左辺)\(=p+p=2p=\)(右辺)
(ⅱ) \({\large \frac{1}{2}}≦q<1\) のとき
\(p+{\large \frac{1}{2}}≦p+q<p+1\) となり
\([x]=p\)
\(p+1≦p+q+{\large \frac{1}{2}}<p+{\large \frac{3}{2}}\) となり
\(\left[x+{\large \frac{1}{2}}\right]=p+1\)
\(2p≦2p+2q<2p+2\) となり
\([2x]=2p+1\)
よって、
(左辺)\(=p+p+1=2p+1=\)(右辺)
したがって、(ⅰ)と(ⅱ)より、
\([x]+\left[x+{\large \frac{1}{2}}\right]=[2x]\) [終]
7
\({\small (1)}~1~,~2~,~-4\)
\({\small (2)}~\)[証明] 任意の実数 \(x\) を \(p\) を整数、\(q\) を \(0≦q<1\) として \(x=p+q\) とすると、
(ⅰ) \(0≦q<{\large \frac{1}{2}}\) のとき
\(p≦p+q<p+{\large \frac{1}{2}}\) となり
\([x]=p\)
\(p+{\large \frac{1}{2}}≦p+q+{\large \frac{1}{2}}<p+1\) となり
\(\left[x+{\large \frac{1}{2}}\right]=p\)
\(2p≦2p+2q<2p+1\) となり
\([2x]=2p\)
よって、
(左辺)\(=p+p=2p=\)(右辺)
(ⅱ) \({\large \frac{1}{2}}≦q<1\) のとき
\(p+{\large \frac{1}{2}}≦p+q<p+1\) となり
\([x]=p\)
\(p+1≦p+q+{\large \frac{1}{2}}<p+{\large \frac{3}{2}}\) となり
\(\left[x+{\large \frac{1}{2}}\right]=p+1\)
\(2p≦2p+2q<2p+2\) となり
\([2x]=2p+1\)
よって、
(左辺)\(=p+p+1=2p+1=\)(右辺)
したがって、(ⅰ)と(ⅱ)より、
\([x]+\left[x+{\large \frac{1}{2}}\right]=[2x]\) [終]
3章 図形の性質
p.150
1
[証明]

線分 \({\rm PC}\) 上に \({\rm BP=CQ}\) となる点 \({\rm Q}\) をとると、
\(\triangle {\rm ABP}\) と \(\triangle {\rm ACQ}\) において、
\({\rm BP=CQ}\) (仮定)
\({\rm AB=AC}\) (正三角形の辺)
四角形 \({\rm ABPC}\) は円に内接するので、
\(\angle{\rm ABP}=\angle{\rm ACQ}\) (外角)
よって、
\(\triangle{\rm ABP}\equiv\triangle{\rm ACQ}\)
対応する角は等しいので、
\(\angle{\rm APB}=\angle{\rm AQC}\)
また、円周角の定理より、
\(\angle{\rm APB}=\angle{\rm ACB}=60^\circ\)
よって、\(\angle{\rm AQC}=60^\circ\) …①
また、円周角の定理より、
\(\angle{\rm ABC}=\angle{\rm APC}=60^\circ\) …②
①、②より、\(\triangle {\rm APQ}\) は正三角形となる
したがって、
\({\rm AP=PC+CQ}\)
\({\rm CQ=BP}\) より、
\({\rm AP=BP+CP}\) [終]
1
[証明]
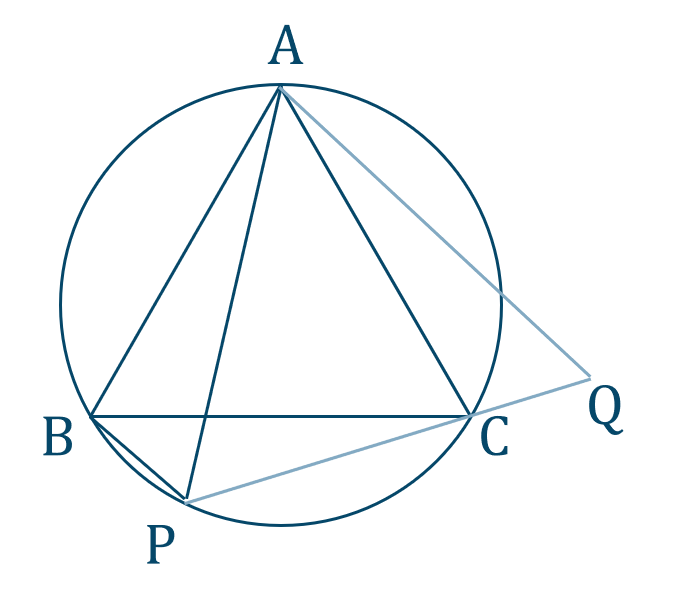
線分 \({\rm PC}\) 上に \({\rm BP=CQ}\) となる点 \({\rm Q}\) をとると、
\(\triangle {\rm ABP}\) と \(\triangle {\rm ACQ}\) において、
\({\rm BP=CQ}\) (仮定)
\({\rm AB=AC}\) (正三角形の辺)
四角形 \({\rm ABPC}\) は円に内接するので、
\(\angle{\rm ABP}=\angle{\rm ACQ}\) (外角)
よって、
\(\triangle{\rm ABP}\equiv\triangle{\rm ACQ}\)
対応する角は等しいので、
\(\angle{\rm APB}=\angle{\rm AQC}\)
また、円周角の定理より、
\(\angle{\rm APB}=\angle{\rm ACB}=60^\circ\)
よって、\(\angle{\rm AQC}=60^\circ\) …①
また、円周角の定理より、
\(\angle{\rm ABC}=\angle{\rm APC}=60^\circ\) …②
①、②より、\(\triangle {\rm APQ}\) は正三角形となる
したがって、
\({\rm AP=PC+CQ}\)
\({\rm CQ=BP}\) より、
\({\rm AP=BP+CP}\) [終]
p.150
2
\({\small (1)}~\)[証明]

\(\triangle {\rm PAO}\) と \(\triangle {\rm PBO}\) において、
\({\rm OA=OB}\) (円の半径)
\({\rm PO=PO}\) (共通の辺)
\({\rm PA}\) と \({\rm PB}\) は円の接線であるので、
\({\rm PA=PB}\)
よって、3辺がそれぞれ等しいので、
\(\triangle{\rm PAO}\equiv\triangle{\rm PBO}\)
対応する角は等しいので、
\(\angle{\rm AOP}=\angle{\rm BOP}\)
次に、孤 \({\rm AC}\) と孤 \({\rm BC}\) の円周角が等しいので、
\({\rm AC=BC}\)
\(\triangle {\rm ABC}\) は二等辺三角形となるので、
\(\angle{\rm CAB}=\angle{\rm CBA}\)
\(\triangle {\rm ABC}\) の接弦定理より、
\(\angle{\rm PAC}=\angle{\rm CBA}\)
したがって、
\(\angle{\rm PAC}=\angle{\rm CAB}\) [終]
\({\small (2)}~{\large \frac{12\sqrt{5}}{7}}~,~{\large \frac{10}{7}}\)
2
\({\small (1)}~\)[証明]
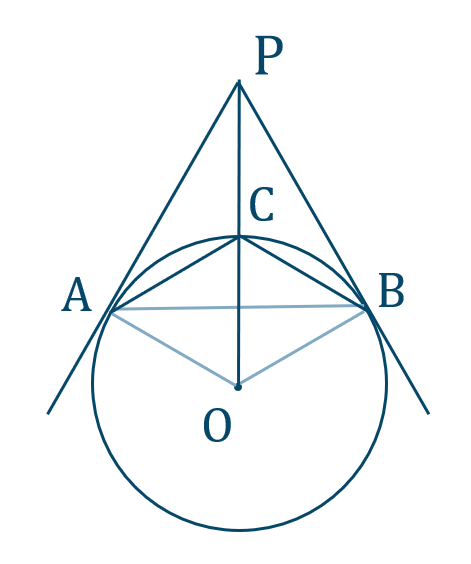
\(\triangle {\rm PAO}\) と \(\triangle {\rm PBO}\) において、
\({\rm OA=OB}\) (円の半径)
\({\rm PO=PO}\) (共通の辺)
\({\rm PA}\) と \({\rm PB}\) は円の接線であるので、
\({\rm PA=PB}\)
よって、3辺がそれぞれ等しいので、
\(\triangle{\rm PAO}\equiv\triangle{\rm PBO}\)
対応する角は等しいので、
\(\angle{\rm AOP}=\angle{\rm BOP}\)
次に、孤 \({\rm AC}\) と孤 \({\rm BC}\) の円周角が等しいので、
\({\rm AC=BC}\)
\(\triangle {\rm ABC}\) は二等辺三角形となるので、
\(\angle{\rm CAB}=\angle{\rm CBA}\)
\(\triangle {\rm ABC}\) の接弦定理より、
\(\angle{\rm PAC}=\angle{\rm CBA}\)
したがって、
\(\angle{\rm PAC}=\angle{\rm CAB}\) [終]
\({\small (2)}~{\large \frac{12\sqrt{5}}{7}}~,~{\large \frac{10}{7}}\)
p.150
3
\({\large \frac{\sqrt{3}}{2}}~,~{\large \frac{\sqrt{3}}{6}}\)
3
\({\large \frac{\sqrt{3}}{2}}~,~{\large \frac{\sqrt{3}}{6}}\)
p.150
4
\({\small (1)}~1\) \({\small (2)}~\sqrt{3}\) \({\small (3)}~{\large \frac{2\sqrt{3}}{3}}\)
4
\({\small (1)}~1\) \({\small (2)}~\sqrt{3}\) \({\small (3)}~{\large \frac{2\sqrt{3}}{3}}\)
資料 集合
p.151
問1
\({\small (1)}~\in~,~\notin\) \({\small (2)}~\notin~,~\in\)
問1
\({\small (1)}~\in~,~\notin\) \({\small (2)}~\notin~,~\in\)
p.152
問2
\({\small (1)}~\{2,3,5,7\}\)
\({\small (2)}~\{1,3,5,7,\cdots,99\}\)
\({\small (3)}~\{-2,2\}\)
\({\small (4)}~\{10,15,20,\cdots\}\)
問2
\({\small (1)}~\{2,3,5,7\}\)
\({\small (2)}~\{1,3,5,7,\cdots,99\}\)
\({\small (3)}~\{-2,2\}\)
\({\small (4)}~\{10,15,20,\cdots\}\)
p.152
問3
\({\small (1)}~\{~x~|~x\)は \(11\) 以下の素数\(~\}\)
\({\small (2)}~\{~2x-1~|~x\)は \(500\) 以下の自然数\(~\}\)
→ 集合の表し方と要素
問3
\({\small (1)}~\{~x~|~x\)は \(11\) 以下の素数\(~\}\)
\({\small (2)}~\{~2x-1~|~x\)は \(500\) 以下の自然数\(~\}\)
→ 集合の表し方と要素
p.153
問4
\({\rm A~,~C~,~D}\)
問4
\({\rm A~,~C~,~D}\)
p.154
問6
\({\small (1)}~{\rm A}\cap{\rm B}=\{2,3,5\}\)
\(~~~~~{\rm A}\cup{\rm B}=\{1,2,3,4,5,7\}\)
\({\small (2)}~{\rm A}\cap{\rm B}=\{1,2,4,8\}\)
\(~~~~~{\rm A}\cup{\rm B}=\{1,2,3,4,6,8,12,16,24,32\}\)
問6
\({\small (1)}~{\rm A}\cap{\rm B}=\{2,3,5\}\)
\(~~~~~{\rm A}\cup{\rm B}=\{1,2,3,4,5,7\}\)
\({\small (2)}~{\rm A}\cap{\rm B}=\{1,2,4,8\}\)
\(~~~~~{\rm A}\cup{\rm B}=\{1,2,3,4,6,8,12,16,24,32\}\)
p.155
問7
\({\rm A}\cap{\rm B}\cap{\rm C} =\{2,4\}\)
\({\rm A}\cup{\rm B}\cup{\rm C} =\{1,2,3,4,5,6,8,10,16\}\)
→ 共通部分と和集合
問7
\({\rm A}\cap{\rm B}\cap{\rm C} =\{2,4\}\)
\({\rm A}\cup{\rm B}\cup{\rm C} =\{1,2,3,4,5,6,8,10,16\}\)
→ 共通部分と和集合
p.155
問8
\(\phi,\{3\} ,\{4\} ,\{5\} \)
\(\{3,4\} ,\{4,5\} ,\{3,5\} ,\{3,4,5\} \)
問8
\(\phi,\{3\} ,\{4\} ,\{5\} \)
\(\{3,4\} ,\{4,5\} ,\{3,5\} ,\{3,4,5\} \)
p.156
問9
\({\small (1)}~\{1,3,5,7,8,9\}\)
\({\small (2)}~\{2,6\}\)
\({\small (3)}~\{1,2,3,5,6,7,8,9\}\)
\({\small (4)}~\{1,2,3,5,6,7,8,9\}\)
問9
\({\small (1)}~\{1,3,5,7,8,9\}\)
\({\small (2)}~\{2,6\}\)
\({\small (3)}~\{1,2,3,5,6,7,8,9\}\)
\({\small (4)}~\{1,2,3,5,6,7,8,9\}\)
p.156
問10
\(\overline {{\rm A}}\) と \(\overline {{\rm B}}\) はそれぞれ次のようになる


したがって、\({\rm A}\subset{\rm B}\) ならば \(\overline {{\rm A}}\supset\overline {{\rm B}}\) である
問10
\(\overline {{\rm A}}\) と \(\overline {{\rm B}}\) はそれぞれ次のようになる
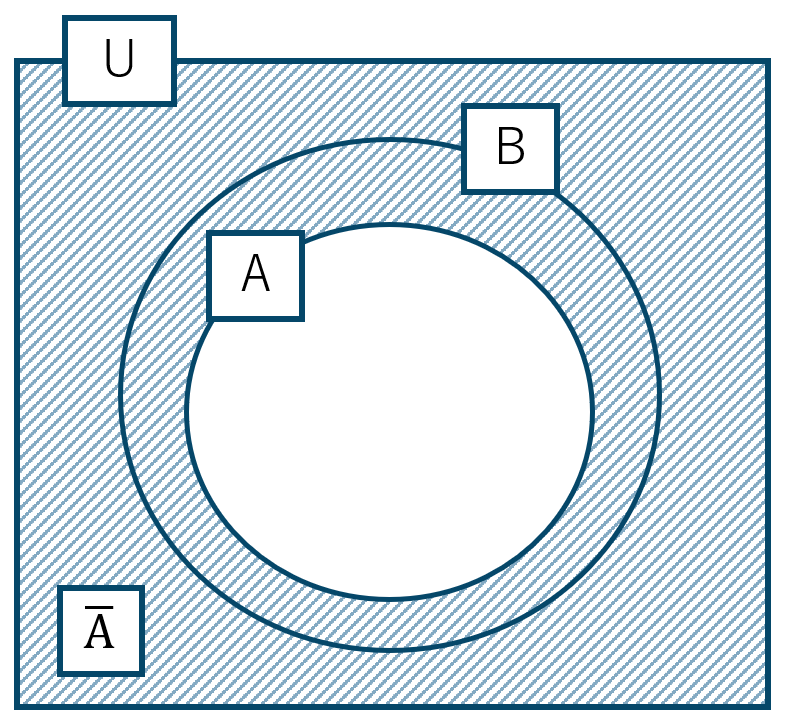
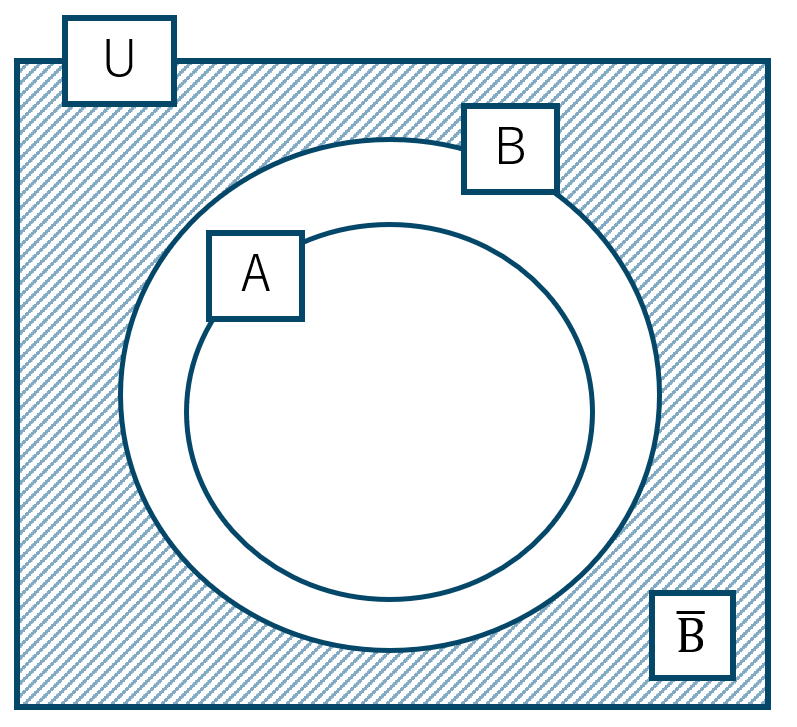
したがって、\({\rm A}\subset{\rm B}\) ならば \(\overline {{\rm A}}\supset\overline {{\rm B}}\) である
p.157
問11
全体集合 \(\rm U\) とその部分集合 \({\rm A}~,~{\rm B}\) において、
\( \overline {{\rm A}} \cup \overline {{\rm B}} \) をベン図で表すと、

この2つの和集合となるので、

これは集合 \( {\rm A}\cap {\rm B} \) の補集合となるので、
\(\overline {{\rm A} \cap {\rm B}}=\overline {{\rm A}} \cup \overline {{\rm B}}\)
問11
全体集合 \(\rm U\) とその部分集合 \({\rm A}~,~{\rm B}\) において、
\( \overline {{\rm A}} \cup \overline {{\rm B}} \) をベン図で表すと、
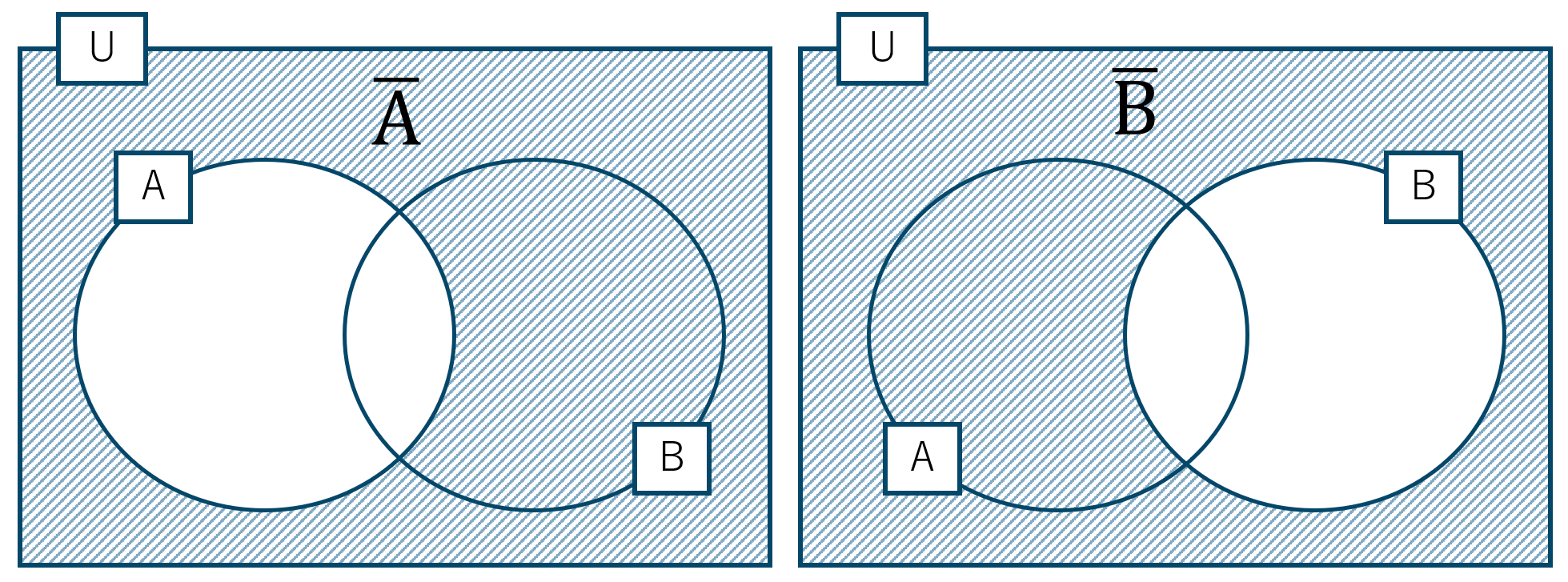
この2つの和集合となるので、
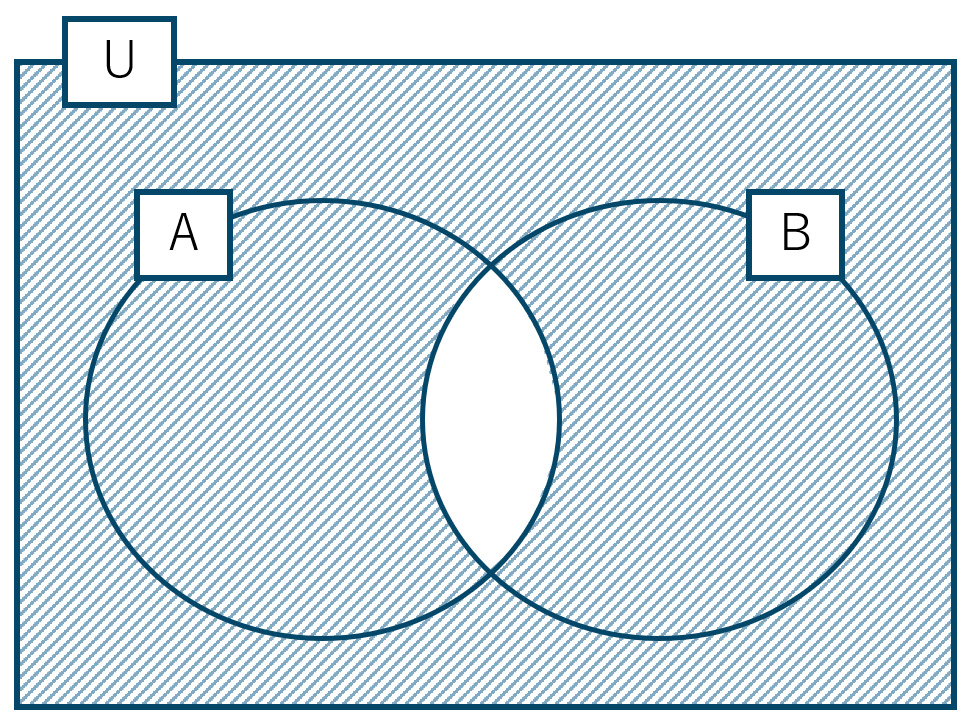
これは集合 \( {\rm A}\cap {\rm B} \) の補集合となるので、
\(\overline {{\rm A} \cap {\rm B}}=\overline {{\rm A}} \cup \overline {{\rm B}}\)
問題
p.157
1
\({\small (1)}~\{~x~|~-1< x≦2\}\)
\({\small (2)}~\{~x~|~x< 5\}\)
\({\small (3)}~\{~x~|~5≦x\}\)
\({\small (4)}~\{~x~|~x≦-1~,~2< x\}\)
1
\({\small (1)}~\{~x~|~-1< x≦2\}\)
\({\small (2)}~\{~x~|~x< 5\}\)
\({\small (3)}~\{~x~|~5≦x\}\)
\({\small (4)}~\{~x~|~x≦-1~,~2< x\}\)


